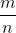对于从n个元素中等可能的选择m个这个问题常见的有两种变体：
1，n是已知的且相对较小；
2，n是未知的或相对很大；
问题的解法也有相似之处，问题1相对简单一些。
1，解法：从n个元素里面等可能取出一个元素，这比较简单，从剩下的n-1个元素里等可能的取出一个元素，持续该过程知道从n-m+1个元素等可能的取出一个元素。则取出的m个元素是等可能的。下面证明
对于n各元素中的任意一个元素x，它第一次被取出的概率为1/n, 第二次被取出的概率为(n-1)/n * 1/(n-1), 依然为1/n, 依次计算第三次被取出的概率，直到第m次被取出的概率都为1/n, 所以总共取了m次，且是加的关系，最后得该元素被取出的概率为 m/n, 由于这个元素的任意性，则得每个元素被取出的概率相等，都为m/n.
2, 解法：对于问题2，我们先取前m个元素为临时选取的结果，对于第m+1个元素，我们以m/(m+1)的概率选定。若选中了，则从临时结果的m个元素中选取一个用选中的结果替换。继续该过程，到第j个元素，以m/j的概率选定，若选中，则从临时的m个元素中选取一个用选中的元素替换。 下面证明
我们需要证明临时结果中的每个元素的概率始终保持为m/n, 其中n为当前时刻元素的总数。取临时结果中的某个元素x，他在某一刻被以m/j的概率选择，那么下一刻他被保留的概率有两部分组成，第j+1个元素没有被选中的情况，第j+1个元素被选中，但是在从临时结果中选取要被替换的元素时它没有被选中。
异常下去直到第n个元素，被选中的元素的概率为
本文章为转载内容，我们尊重原作者对文章享有的著作权。如有内容错误或侵权问题，欢迎原作者联系我们进行内容更正或删除文章。
