
Attention
秋招接近尾声,我总结了 牛客、WanAndroid 上,有关笔试面经的帖子中出现的算法题,结合往年考题写了这一系列文章,所有文章均与 LeetCode 进行核对、测试。欢迎食用
本文将覆盖 「二进制」 + 「位运算」 和 Lru 方面的面试算法题,文中我将给出:
面试中的题目
解题的思路
特定问题的技巧和注意事项
考察的知识点及其概念
详细的代码和解析
开始之前,我们先看下会有哪些重点案例:

为了方便大家跟进学习,我在 GitHub 建立了一个仓库
现在就让我们开始吧!
矩阵

螺旋矩阵
给定一个包含 m x n 个要素的矩阵,(m 行, n 列),按照螺旋顺序,返回该矩阵中的所有要素。
示例 :
输入:
[
[1, 2, 3, 4],
[5, 6, 7, 8],
[9,10,11,12]
]
输出: [1,2,3,4,8,12,11,10,9,5,6,7]
解题思路
我们定义矩阵的第 k 层是到最近边界距离为 k 的所有顶点。例如,下图矩阵最外层元素都是第 1 层,次外层元素都是第 2 层,然后是第 3 层的。
[[1, 1, 1, 1, 1, 1, 1],
[1, 2, 2, 2, 2, 2, 1],
[1, 2, 3, 3, 3, 2, 1],
[1, 2, 2, 2, 2, 2, 1],
[1, 1, 1, 1, 1, 1, 1]]
对于每层,我们从左上方开始以顺时针的顺序遍历所有元素,假设当前层左上角坐标是 \(\text{(r1, c1)}\),右下角坐标是 \(\text{(r2, c2)}\)。
首先,遍历上方的所有元素 (r1, c),按照 c = c1,...,c2 的顺序。然后遍历右侧的所有元素 (r, c2),按照 r = r1+1,...,r2 的顺序。如果这一层有四条边(也就是 r1 < r2 并且 c1 < c2 ),我们以下图所示的方式遍历下方的元素和左侧的元素。
public List spiralOrder(int[][] matrix) {
ArrayList rst = new ArrayList();
if(matrix == null || matrix.length == 0) {
return rst;
}
int rows = matrix.length;
int cols = matrix[0].length;
int count = 0;
while(count * 2 < rows && count * 2 < cols){
for (int i = count; i < cols - count; i++) {
rst.add(matrix[count][i]);
}
for (int i = count + 1; i < rows - count; i++) {
rst.add(matrix[i][cols - count - 1]);
}
if (rows - 2 * count == 1 || cols - 2 * count == 1) { // 如果只剩1行或1列
break;
}
for (int i = cols - count - 2; i >= count; i--) {
rst.add(matrix[rows - count - 1][i]);
}
for (int i = rows - count - 2; i >= count + 1; i--) {
rst.add(matrix[i][count]);
}
count++;
}
return rst;
}判断数独是否合法
请判定一个数独是否有效。该数独可能只填充了部分数字,其中缺少的数字用 . 表示。
维护一个HashSet用来记同一行、同一列、同一九宫格是否存在相同数字

示例 :
输入:
[
["8","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]
]
输出: false
解释: 除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。
但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
说明:
一个有效的数独(部分已被填充)不一定是可解的。
只需要根据以上规则,验证已经填入的数字是否有效即可。
给定数独序列只包含数字 1-9 和字符 '.' 。
给定数独永远是 9x9 形式的。`
解题思路
一次迭代
首先,让我们来讨论下面两个问题:
如何枚举子数独?
可以使用 box_index = (row / 3) * 3 + columns / 3,其中 / 是整数除法。

如何确保行 / 列 / 子数独中没有重复项?
可以利用 value -> count 哈希映射来跟踪所有已经遇到的值。
现在,我们完成了这个算法的所有准备工作:
遍历数独。
检查看到每个单元格值是否已经在当前的行 / 列 / 子数独中出现过:
如果出现重复,返回 false。
如果没有,则保留此值以进行进一步跟踪。
返回 true。

public boolean isValidSudoku(char[][] board) {
Set seen = new HashSet();
for (int i=0; i<9; ++i) {
for (int j=0; j<9; ++j) {
char number = board[i][j];
if (number != '.')
if (!seen.add(number + " in row " + i) ||
!seen.add(number + " in column " + j) ||
!seen.add(number + " in block " + i / 3 + "-" + j / 3))
return false;
}
}
return true;
}旋转图像
给定一个N×N的二维矩阵表示图像,90度顺时针旋转图像。
示例 :
输入: [[1,1,0,0],[1,0,0,1],[0,1,1,1],[1,0,1,0]]
输出: [[1,1,0,0],[0,1,1,0],[0,0,0,1],[1,0,1,0]]
解释: 首先翻转每一行: [[0,0,1,1],[1,0,0,1],[1,1,1,0],[0,1,0,1]];
然后反转图片: [[1,1,0,0],[0,1,1,0],[0,0,0,1],[1,0,1,0]]
说明:
1 <= A.length = A[0].length <= 20
0 <= A[i][j] <= 1
解题思路
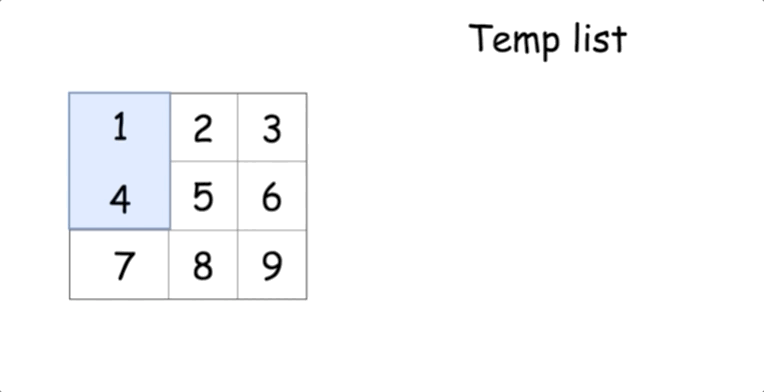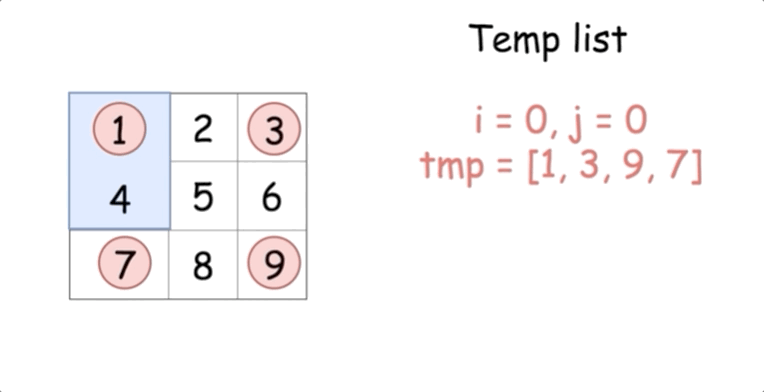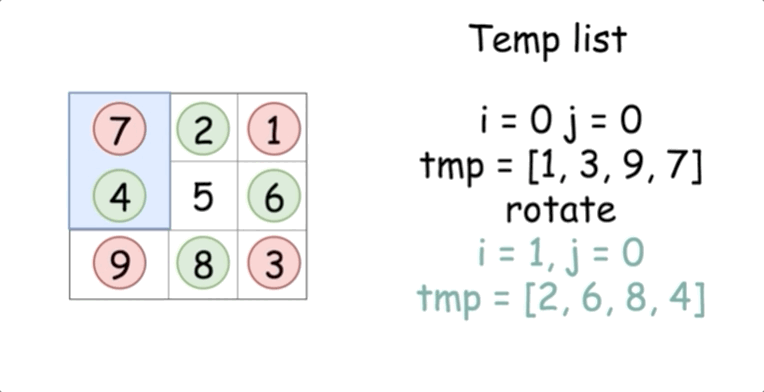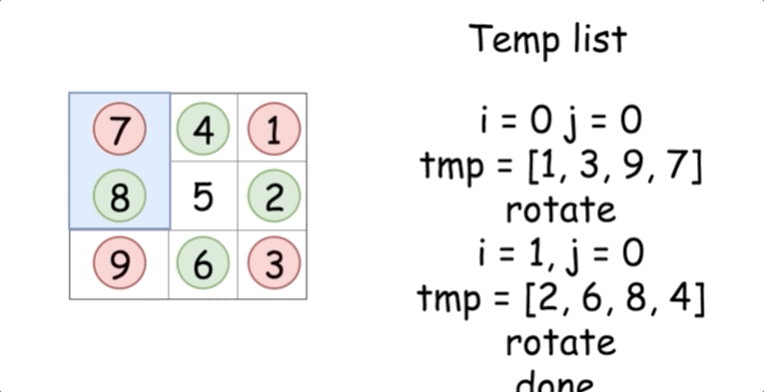
我们先来看看每个元素在旋转的过程中是如何移动的:

这提供给我们了一个思路,将给定的矩阵分成四个矩形并且将原问题划归为旋转这些矩形的问题。

现在的解法很直接 -- 可以在第一个矩形中移动元素并且在 长度为 4 个元素的临时列表中移动它们。
public void rotate(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return;
}
int length = matrix.length;
for (int i = 0; i < length / 2; i++) {
for (int j = 0; j < (length + 1) / 2; j++){
int tmp = matrix[i][j];
matrix[i][j] = matrix[length - j - 1][i];
matrix[length -j - 1][i] = matrix[length - i - 1][length - j - 1];
matrix[length - i - 1][length - j - 1] = matrix[j][length - i - 1];
matrix[j][length - i - 1] = tmp;
}
}
}二进制 / 位运算

优点:
特定情况下,计算方便,速度快,被支持面广
如果用算数方法,速度慢,逻辑复杂
位运算不限于一种语言,它是计算机的基本运算方法
知识点预热
(一)按位与&
两位全为1,结果才为1
0&0=0;0&1=0;1&0=0;1&1=1
例如:51&5 即 0011 0011 & 0000 0101 =0000 0001 因此51&5=1.
特殊用法
(1)清零。如果想将一个单元清零,即使其全部二进制位为0,只要与一个各位都是零的数值相与,结果为零。
(2)取一个数中指定位。
例如:设 X=10101110,取X的低四位,用X&0000 1111=0000 1110即可得到。
方法:找一个数,对应x要取的位,该数的对应位为1,其余位为零,此数与x进行“与运算”可以得到x中的指定位。
(二)按位或 |
只要有一个为1,结果就为1。
0|0=0; 0|1=1;1|0=1;1|1=1;
例如:51|5 即0011 0011 | 0000 0101 =0011 0111 因此51|5=55
特殊用法
常用来对一个数据的某些位置1。
方法:找到一个数,对应x要置1的位,该数的对应位为1,其余位为零。此数与x相或可使x中的某些位置1。
(三)异或 ^
两个相应位为“异”(值不同),则该位结果为1,否则为0
0^0=0; 0^1=1; 1^0=1; 1^1=0;
例如:51^5 即0011 0011 ^ 0000 0101 =0011 0110 因此51^5=54
特殊用法
(1) 与1相异或,使特定位翻转
方法:找一个数,对应X要翻转的位,该数的对应为1,其余位为零,此数与X对应位异或即可。
例如:X=1010 1110,使X低四位翻转,用X^0000 1111=1010 0001即可得到。
(2) 与0相异或,保留原值
例如:X^0000 0000 =1010 1110
(3)两个变量交换值
1.借助第三个变量来实现
C=A;A=B;B=C;
2.利用加减法实现两个变量的交换
A=A+B;B=A-B;A=A-B;
3.用位异或运算来实现,也是效率最高的
原理:一个数异或本身等于0 ;异或运算符合交换律
A=A^B;B=A^B;A=A^B
(四)取反与运算~
对一个二进制数按位取反,即将0变为1,1变0
~1=0 ;~0=1
(五)左移<<
将一个运算对象的各二进制位全部左移若干位(左边的二进制位丢弃,右边补0)
例如: 2<<1 =4 10<<1=100
若左移时舍弃的高位不包含1,则每左移一位,相当于该数乘以2。
例如:
11(1011)<<2= 0010 1100=22
11(00000000 00000000 00000000 1011)整形32bit
(六)右移>>
将一个数的各二进制位全部右移若干位,正数左补0,负数左补1,右边丢弃。若右移时舍高位不是1(即不是负数),操作数每右移一位,相当于该数除以2。
左补0还是补1得看被移数是正还是负。
例如:4>>2=4/2/2=1
-14(即1111 0010)>>2 =1111 1100=-4
(七)无符号右移运算>>>
各个位向右移指定的位数,右移后左边空出的位用零来填充,移除右边的位被丢弃。
例如:-14>>>2
(即11111111 11111111 11111111 11110010)>>>2
=(00111111 11111111 11111111 11111100)=1073741820

只出现一次的数字
给出 2 * n + 1个数字,除其中一个数字之外其他每个数字均出现两次,找到这个数字。
异或运算具有很好的性质,相同数字异或运算后为0,并且具有交换律和结合律,故将所有数字异或运算后即可得到只出现一次的数字。
示例 :
输入: [4,1,2,1,2]
输出: 4
解题思路
如果我们对 0 和二进制位做 XOR 运算,得到的仍然是这个二进制位
\(a \oplus 0 = a\) \(a⊕0=a\)
如果我们对相同的二进制位做 XOR 运算,返回的结果是 0
\(a \oplus a = 0\) \(a⊕a=0\)
XOR 满足交换律和结合律
\(a \oplus b \oplus a = (a \oplus a) \oplus b = 0 \oplus b = ba⊕b⊕a=(a⊕a)⊕b=0⊕b=b\)
所以我们只需要将所有的数进行 XOR 操作,得到那个唯一的数字。
public int singleNumber(int[] A) {
if(A == null || A.length == 0) {
return -1;
}
int rst = 0;
for (int i = 0; i < A.length; i++) {
rst ^= A[i];
}
return rst;
}复杂度分析
时间复杂度: O(n) 。我们只需要将 \(\text{nums}\) 中的元素遍历一遍,所以时间复杂度就是 \(\text{nums}\) 中的元素个数。
空间复杂度:O(1) 。
格雷编码
格雷编码是一个二进制数字系统,在该系统中,两个连续的数值仅有一个二进制的差异。给定一个非负整数 n ,表示该代码中所有二进制的总数,请找出其格雷编码顺序。一个格雷编码顺序必须以 0 开始,并覆盖所有的 2n 个整数。例子——输入:2;输出:[0, 1, 3, 2];解释: 0 - 00,1 - 01,3 - 11,2 - 10
解题思路
格雷码生成公式:G(i) = i ^ (i >> 2)
public ArrayList grayCode(int n) {
ArrayList result = new ArrayList();
for (int i = 0; i < (1 << n); i++) {
result.add(i ^ (i >> 1));
}
return result;
}其他

整数反转
将一个整数中的数字进行颠倒,当颠倒后的整数溢出时,返回 0 (标记为 32 位整数)。
示例 :
输入: -123
输出: -321
解题思路
利用除 10 取余的方法,将最低位和最高倒序输出即可
public int reverseInteger(int n) {
int reversed_n = 0;
while (n != 0) {
int temp = reversed_n * 10 + n % 10;
n = n / 10;
if (temp / 10 != reversed_n) {
reversed_n = 0;
break;
}
reversed_n = temp;
}
return reversed_n;
}LRU缓存策略
运用你所掌握的数据结构,设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作: 获取数据 get 和 写入数据 put 。
获取数据 get(key) - 如果密钥 (key) 存在于缓存中,则获取密钥的值(总是正数),否则返回 -1。
写入数据 put(key, value) - 如果密钥不存在,则写入其数据值。当缓存容量达到上限时,它应该在写入新数据之前删除最近最少使用的数据值,从而为新的数据值留出空间。
示例:
LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );
cache.put(1, 1);
cache.put(2, 2);
cache.get(1); // 返回 1
cache.put(3, 3); // 该操作会使得密钥 2 作废
cache.get(2); // 返回 -1 (未找到)
cache.put(4, 4); // 该操作会使得密钥 1 作废
cache.get(1); // 返回 -1 (未找到)
cache.get(3); // 返回 3
cache.get(4); // 返回 4解题思路
解法一:
自定义数据结构:
实现一个链表用于记录缓存,并处理调用使用频率
定义一个 HashMap 用于记录缓存内容
public class LRUCache {
private class Node{
Node prev;
Node next;
int key;
int value;
public Node(int key, int value) {
this.key = key;
this.value = value;
this.prev = null;
this.next = null;
}
}
private int capacity;
private HashMap hs = new HashMap();
private Node head = new Node(-1, -1);// 头
private Node tail = new Node(-1, -1);// 尾
public LRUCache(int capacity) {
this.capacity = capacity;
tail.prev = head;
head.next = tail;
}
public int get(int key) {
if( !hs.containsKey(key)) { //key找不到
return -1;
}
// remove current
Node current = hs.get(key);
current.prev.next = current.next;
current.next.prev = current.prev;
// move current to tail
move_to_tail(current);//每次get,使用次数+1,最近使用,放于尾部
return hs.get(key).value;
}
public void set(int key, int value) {//数据放入缓存
// get 这个方法会把key挪到最末端,因此,不需要再调用 move_to_tail
if (get(key) != -1) {
hs.get(key).value = value;
return;
}
if (hs.size() == capacity) {//超出缓存上限
hs.remove(head.next.key);//删除头部数据
head.next = head.next.next;
head.next.prev = head;
}
Node insert = new Node(key, value);//新建节点
hs.put(key, insert);
move_to_tail(insert);//放于尾部
}
private void move_to_tail(Node current) { //移动数据至尾部
current.prev = tail.prev;
tail.prev = current;
current.prev.next = current;
current.next = tail;
}
}解法二:
题目要求实现 LRU 缓存机制,需要在 O(1)时间内完成如下操作:
获取键 / 检查键是否存在
设置键
删除最先插入的键
前两个操作可以用标准的哈希表在 O(1) 时间内完成。
有一种叫做有序字典的数据结构,综合了哈希表和链表,在 Java 中为 LinkedHashMap。
下面用这个数据结构来实现。
class LRUCache extends LinkedHashMap{
private int capacity;
public LRUCache(int capacity) {
super(capacity, 0.75F, true);
this.capacity = capacity;
}
public int get(int key) {
return super.getOrDefault(key, -1);
}
public void put(int key, int value) {
super.put(key, value);
}
@Override
protected boolean removeEldestEntry(Map.Entry eldest) {
return size() > capacity;
}
}复杂度分析
时间复杂度:对于 put 和 get 操作复杂度是 \(O(1)\),因为有序字典中的所有操作:
get/in/set/move_to_end/popitem(get/containsKey/put/remove)都可以在常数时间内完成。
空间复杂度:\(O(capacity)\),因为空间只用于有序字典存储最多 capacity + 1 个元素。
Attention
为了提高文章质量,防止冗长乏味
下一部分算法题
本片文章篇幅总结越长。我一直觉得,一片过长的文章,就像一堂超长的 会议/课堂,体验很不好,所以我打算再开一篇文章
在后续文章中,我将继续针对链表 栈 队列 堆 动态规划 矩阵 位运算 等近百种,面试高频算法题,及其图文解析 + 教学视频 + 范例代码,进行深入剖析有兴趣可以继续关注
不求快,只求优质,每篇文章将以 2 ~ 3 天的周期进行更新,力求保持高质量输出






















