本节我们介绍可变编解码器内部运行的数学原理,了解了这些原理,我们才能明白可变编解码器的设计思想。首先我们需要介绍信息量的概念,它来自于信息论(1):
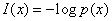
在(1)中x代表我们实验的结果,p(x)表示实验出现给定结果的概率,例如丢一枚硬币,那么我们用x=1表示出现正面,x=0表示出现负面。于是根据(1)一次丢硬币后实验对应的信息量就是-log(1/2) = 1,我们常用比特来作为信息量的单位。第二个需要介绍的概念叫信息熵,它的公式如下所示(2):
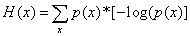
公式(2)计算后得到的值越大表明一个系统状态就越混乱。假设我们当前有两个系统,第一个系统出现结果x的概率是p(x),第二个系统出现结果x的概率是q(x),那么我们用如下公式来量化两个系统的差异性(3):

对公式(3)而言,它暗含了一种相对性,(3)表示的是系统1相对于系统2的差异性,如果是系统2相对于系统1的差异性那就是 ,这里需要注意的是,通常情况下我们有 :
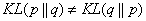
如果经过公式(3)计算出来的值越小就意味着两个系统越相似。举个例子,在系统1中我们用x=1表示抛硬币出现正面,x=2表示出现反面。在系统2中我们用x的值对应丢骰子正面朝上的点数。由此系统1运行的结果和系统2中正面朝上是点1和点2这两种情况就可以相互比较,显然当系统2正面朝上的点不是1和2时的情况就不能与系统1比较。系统1中出现不同结果的概率是1/2,系统2中出现两种不同结果的概率是1/6,由此我们可以代入(3)计算两种系统的差异。
但如果我们把系统2中用x=1表示正面朝上的点时奇数,x=2表示正面朝上的点是偶数,那么系统2中x=1和x=2的概率都是1/2,于是代入(3)后得到结果为0,也就是在这种观察角度下,丢硬币和丢骰子完全是一回事,同时从公式(3)中我们还可以确定的一点是 :

前面提到的这些理论将会被用于给定系统的概率分布推导上。假设我们有一个系统,它运行的结果用x表示,但x出现的结果由系统内部的一个无法观察到的变量z来控制,因此两个变量的关系如下图所示:

上图中不可见变量决定可见变量由于我们只能看到结果x,看不到变量z,因此我们就希望通过x的取值去推导z取值的概率。我们看一个思想实验,例如给定一个实验有三枚硬币,第一枚硬币正面出现的概率是1/2,第二枚硬币正面出现的概率是1/3,第三枚硬币证明出现的概率是1/4.
我们用z来表示哪一枚硬币被选择,例如z=1表示第一枚硬币被选中。同时我们用x表示抛硬币一万次后出现正面的次数。如果我们不知道z的取值,但知道x的取值,那么我们如何根据x的取值来判断z取值1,2,3对应的概率呢。
如果我们使用P(z|x)表示给定x的值时,z取值的概率,那么根据概率论就有(4):
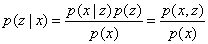
通常我们有(5):

例如在例子中,我们假设三枚硬币被选中的概率相等,那么就有p(z=1)=p(z=2)=p(z=3)=1/3,假设x = 5,那么我们就可以根据公式(5)计算p(x=5)的概率,因为我们知道当前选中的是那一枚硬币时,也就是z确定时计算P(x|z)也很容易。因此根据(4)就可以从观察到的x反向推导出z的取值概率,其中(4)也称为贝叶斯公式。问题在于,通常情况下p(x)很难直接计算,特别是如果z是一个维度为d的向量时,公式(5)就得换成d维积分。
由于p(x)计算困难,我们可以使用另一个相对容易计算的概率函数q(x)通过一些调整后去模拟p(x),如果q(x)模拟效果越好,那么KL(q||p)的值就越小。读者如果对微积分有所了解,知道泰勒展开,那么对于函授sin(x)在点0处展开为(6):

显然sin(0.015)很不好计算,但是使用(6)右边公式进行计算就容易得多。于是我们可以把sin(x)看作p(x),然后我们可以用 或 来模拟p(x),显然后者的模拟效果更好,因为将它代入到(3)后所得结果更小。通过这种变换我们可以降低问题的难度,也就是拿相对简单的函数取模拟逼近复杂函数从而得到我们想要的计算结果。回到公式(4),由于p(x)通常很难计算,因此导致p(z|x)很难计算,这意味着我们很难通过观察x去推导变量z的可能性。于是我们就想方设法使用一个容易计算的函数q(z|x)去模拟p(z|x),因此我们的任务是找到合适的q(z),然后不断的对它进行调整使得KL(q||p)的值变小,当KL(q(z)||p(z|x))取得最小值时,我们就得到了最佳逼近效果。根据公式(3)并结合(4)我们有(7):

由于对数运算中的乘法和除法可以转换为加法和减法,因此我们有(8):

这里需要注意的是,由于

,所以有

,同时由于x对应我们观察到的结果,所以它不再是一个变量,所以log(p(x))是一个常量。由此结合(8)我们就有(9):

我们的目标是计算

的最小值,同时(9)的等号左边是一个常量,因此我们可以把目标转换为计算

的最大值。我们继续把这一项展开就有(10):

注意到(11):

于是我们就有(12):

这意味着我们要最大化

,同时最小化

,这些推导如何与我们要理解的编解码器联系起来呢,我们看下图就可以有所理解:

上图是可变编解码器模型,根据上图的编解码器模型,它接收图片x后,将其转换为向量z,然后再将向量z转换为x,由于z转换回x时可能会存有误差因此我们用x’替代。由于模型是我们设定的,因此我们就可以规定x到z和z到x的规律。
编码器希望接收x后将它转换为对应的z,但问题在于我们无法确定对应关系p(z|x),因此我们使用容易计算的关系q(z|x)来模拟它,这里我们选取正太分布函数来替代。一旦z确定之后,由z到x的关系就很容易确定。
就好像我们前面的思想实验中,一旦知道z的值,我们就知道哪枚硬币被选中,由此我们就可以估计x对应的值,当然x是理论值,实验后出现的具体值肯定与理论上的x有差异,因此我们用x’代表实验后的具体值。
例如z=1,那么随机变量x对应抛一万次后出现正面的次数,理论上x应该等于1/2,但抛一万次后,出现正面的次数可能是4990次,因此x’就对应0.49,。对应到图12-13,解码器就相当于模拟硬币抛一万次的过程。
如果我们假设有了z之后,生成x的过程满足正太随机分布,同时我们注意到解码器实际上是把输入它的z经过一系列运算后生成x’,这系列运算时确定性的流程,也就是我们把同一个z输入解码器十次,那么解码器输出的结果十次都相同。
因此z与x’存在确定的函数关系,因此我们可以把关系p(x|z)换成p(x|x’),由于我们假设p(x|z)满足正太分布,因此p(x|x’)也就满足正太分布。我们知道正太分布函数形式为(13):

如果我们把令

,那么(13)就变成(14):

于是p(x|x’)就是要对(14)进行积分运算,可以肯定的是积分结果一定包含

。由于 中对p(x|z)进行对数运算,由于p(x|z)可以对应为p(x|x’),因此它相当于对(13)积分后的结果做对数运算。
又因为p(x|x’)含有

,做对数运算后有

,如果我们想让

变大,我们就得让

变小,这就要求我们解码器生成的x’与输入编码器的x差方和要尽可能的小。接下来我们看看如何理解

,其中p(z)表示在没有看到x的情况下z的分布概率, 这里我们可以设置z的先验概率满足正太分布,这类似于我们是思想实验里面那个选择硬币的人,我们可以根据自己的喜好来决定硬币如何选择。q(z|x)对应编码器接收x后如何生成z,于是我们就得调整编码器的行为,让它输出结果尽可能像一个正太分布函数。由此我们把编解码网络修改成如下图所示结构:

由于正太分布受两个关键变量的影响,一个是均值 ,另一个是方差 ,这两个变量一旦确定,整个随机过程就能确定,因此要让编码器模拟正太分布函数,关键在于让它生成两个关键变量,使得它们决定的正太分布与要模拟的均值为0方差为1的正太分布在KL值上尽可能小。
注意到在上图添加了一个随机变量

,它乘以编码器生成的方差,然后加上生成的均值形成要输入给解码器的中间向量z,这个过程叫随机抽样,形象化的说这就相当于编码器打造了一枚满足特定概率的硬币,随机抽样就是抛这枚硬币获取结果。
随机抽样引入了不确定性,就好像每次抛硬币得到的结果都可能不一样,但这些不确定性肯定遵循给定概率。现在我们看看如何训练编码器让它满足(10)中第二部分取值尽可能小。由于编码器模拟的是正太分布函数

,p(z)对应

,代入有(14):

把对应q(z|x)和p(z)对应的函数代入(14)就有(15):

注意到

,所以

,同时

,根据方差公式

,由于x是满足正太随机分布的变量,因此有

.
因此我们有

,最后一部分

,如果我们做一个变量替换,令

,于是有(16):

注意到

是均值为0,方差为1的正态分布密度函数,因此var(T)=1,E[T]=0,于是有(17):

由此我们得到(18):

在实践中,我们通常让编码器不直接输出 而是输出 ,这样训练出来的网络效果更好,因此(18)就变成(19):

由于网络处理的是高维数据,因此我们可以根据下图来替换可变编解码网络与普通网络的区别:

对于以前的编解码网络而言,它对应上图左边情况,它把给定数据(在我们例子里就是手写数字图片)与空间中的单独一点对应起来,而编解码网络像上图右边,它把数据与空间以某一点 为圆心, 为半径内的所有点进行对应。
公众号:






















