上篇讲了nearest-neighbor(最近邻插值)。这篇说cubic interpolation(三次插值),之前说过,插值就是用已知的点模拟一个方程,然后求未知点。之前讲的插值是线性的。cubic interpolation就是求一个三次的方程。它的思想就是把已知的数分为一个一个小区间,人拟合到曲线上去。就是一个多分段函数高阶函数(此处的阶数为3)。给一个文档上的图可能比较清楚。

把区间[a,b]分为n个区间[x0,x1],[x1,x2].....[xn-1,xn]共有n+1个点。其中x0=a,xn=b。把函数定义为

如果满足一下三个条件,我们就称之为三次样条函数
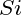
(x)1,在每个分段小区间 [xi,xi+1] 上,
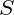
(x)=
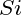
(x)是一个三次方程2,满足插值条件,即
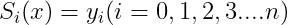
3, 曲线光滑,即 一阶,二阶导存在且连续
现在就是求目标就是求每一段的4个未知数。一共有n段所以有4n个未知数。那么我们需要4n个方程。现在我们就开始列这些方程
首先 在区间[xi,xi+1]上
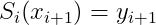
,在区间[xi+1,x+2]中
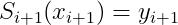
。共有n-1个区间,所以有2(n-1)个方程,加上两个端点就有2个方程。其实简单的想就是n个区间[x0,x1],[x1,x2].....[xn-1,xn]共有n+1个点。每个点用了两次,2(n+1),但是第一个点和最后一个点只用了一次,所以减二。所以为2n。 还差2n个方程,现在就是每一个连接点处的一阶导和二阶导是相等的。

,

。这里有2(n-1)个方程。现在我们还差2个方程。
有3种边界条件:
1 自然边界: 指定端点二阶导数为0,

2 固定边界:假设两个边界值分别为A和B,

3 非节点边界:强制第一个插值点的三阶导数值等于第二个点的三阶导数值,最后第一个点的三阶导数值等于倒数第二个点的三阶导数值.


好我们四个方程就全部列完了。现在就开始求解吧。

1 用

得出

2 用

由

得出

3 用

可得

因为

,所以

4 用

得出

设

,由

,得出
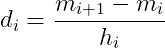
5 由


,

,
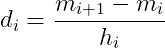
得出

6 因为

,所以

,把

代入其中。
得出

经过上面的6步后,我们构成了关于m的未知线性方程。
我们分别适应,前面边界条件的三种
1 自然边界头尾的边界值都为0,首尾两端没有受到任何让它们弯曲的力。二阶导数为0,于是看把

和

写成矩阵相乘的形式。

(mi表示的是二阶求导)和

都等于0,把矩阵写成:


2 固定边界


系数矩阵为

3 当为 非节点边界时,同理可得系数矩阵为:

好了这个就是三次插值,总的来说就是求一个在三阶函数的点,用已知的点来划分区域,形成分段多阶函数。求4n个未知数。列4n个方程,最后用矩阵表示。下一篇讲bicubic interpolation。





















