线性模型
- 1. 用于回归的线性模型
- 2. 线性回归(OLS普通最小二乘法)
- 3. 岭回归
- 4. Lasso
线性模型是实践中广泛应用的一类模型。线性模型利用输入特征的线性函数进行预测。
这里就在不写需要什么环境了,可以翻看之前的笔记。
1. 用于回归的线性模型
对于回归问题,线性模型预测的一般公式如下:
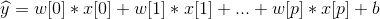
其中w是斜率,b是y轴偏移。
我们在一维wave数据集上学习参数w和b。运行代码如下:
import matplotlib.pyplot as plt
import mglearn
mglearn.plots.plot_linear_regression_wave()
plt.show()输出:
w[0]: 0.393906 b: -0.031804效果图:

用于回归的线性模型可以表示为这样的回归模型:对单一特征的预测结果是一条直线,两个特征的时候是一个平面,或者更多特征的时候是一个超平面。
有许多不同的线性回归模型。这些模型之间的区别在于如何从训练数据中学习参数w和b,以及如何控制模型的复杂度。
2. 线性回归(OLS普通最小二乘法)
OLS是回归问题的最简单也是最经典的线性方法。
OLS寻找参数w和b,使得对训练集的预测值与真实的回归目标值y之间的均方误差最小。
均方误差——是预测值与真实值之差的平方出意样本数。
OLS没有参数,这是一个优点,但也因此无法控制模型的复杂度。
运行代码如下:
import mglearn
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
X,y=mglearn.datasets.make_wave(n_samples=60)
#random_state参数指定随机数生成器的种子,使每次拆分的数据集相同
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=42)
lr = LinearRegression().fit(X_train, y_train)
print("lr.coef_: {}".format(lr.coef_))#w(权重或系数)被保存在coef_属性中
print("lr.intercept_: {}".format(lr.intercept_))#b(偏移或截距)被保存在intercept_属性中输出:
lr.coef_: [0.39390555]
lr.intercept_: -0.031804343026759746- 训练后可通过coef_和intercept_方法得到其斜率w与截距b
- 其中coef_返回Numpy数组,intercept_返回浮点数
- 对于高维度的数据集,当可用数据较少时,线性回归泛化能力较差,当数据增多时,性能增强
下面让我们看一下训练集和测试集的性能
print("Training set score: {:.2f}".format(lr.score(X_train,y_train)))
print("Test set score: {:.2f}".format(lr.score(X_test,y_test)))输出:
Training set score: 0.67
Test set score: 0.66我们可以看到,训练集和测试集上的分数非常接近,这说明可能存在欠拟合。
下面我们看一下LinearRegression在更复杂的数据集上的表现。例如在波士顿房价数据集,记住这个数据集有506个样本和105个导出特征。
运行代码如下:
import matplotlib.pyplot as plt
import mglearn
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
X,y=mglearn.datasets.load_extended_boston()
#random_state参数指定随机数生成器的种子,使每次拆分的数据集相同
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)
lr = LinearRegression().fit(X_train, y_train)
print("Training set score: {:.2f}".format(lr.score(X_train,y_train)))
print("Test set score: {:.2f}".format(lr.score(X_test,y_test)))输出:
Training set score: 0.95
Test set score: 0.61比较一下,我们可以发现训练集上的预测非常准确,但是在测试集上的R²就要低上很多。
- 训练集和测试集之间的性能差异是过拟合的明显标志
所以,我们下面要学习一个可以控制复杂度的模型。
3. 岭回归
岭回归也是一种用于回归的线性模型,其预测公式与普通最小二乘法相同,但是在岭回归中,对系数w的选择不仅要在训练数据上得到好的效果,还要拟合附加约束。
我们希望w的所有元素都接近于0,这意味着每个特征对输出的影响尽可能小(即斜率很小),同时仍给出很好的预测结果,这种约束是正则化的一个例子。
- 正则化:指对模型做显式约束,以避免过拟合
- 岭回归用到的是L2正则化
让我们实现一下他对扩展的波士顿房价数据集的效果如何。
运行代码如下:
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
import mglearn
X,y=mglearn.datasets.load_extended_boston()
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)
ridge=Ridge().fit(X_train,y_train)
print("Training set score: {:.2f}".format(ridge.score(X_train,y_train)))
print("Test set score: {:.2f}".format(ridge.score(X_test,y_test)))输出:
Training set score: 0.89
Test set score: 0.75可以看出,Ridge在训练集上的分数,要低于LinearRegression,但是在测试集上的分数更高。
这和我们预期的一致。线性回归对数据存在过拟合。
Ridge是一种越是u行更强的模型,所以不容易过拟合。
- 复杂度更小的模型意味着在训练集上的性能更差,但是泛化性能更好。
Ridge模型的简单性和训练集性能二者对于模型的重要程度可以由我们自己通过alpha参数来指定。
alpha参数默认值为1.0,但是没理由认为这会给出最佳权衡,alpha的最佳设定取决于用到的具体数据集。
- 增大alpha,会使系数w更趋向于0,从而降低训练集性能,但是会提高泛化能力
实例如下:
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
import mglearn
X,y=mglearn.datasets.load_extended_boston()
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)
ridge=Ridge(alpha=10).fit(X_train,y_train)
print("Training set score: {:.2f}".format(ridge.score(X_train,y_train)))
print("Test set score: {:.2f}".format(ridge.score(X_test,y_test)))输出:
Training set score: 0.79
Test set score: 0.64- 减小alpha可以让系数受到的限制变得更小。对于非常小的alpha值,系数几乎没有受到限制,我们得到一个与LinearRegression类似的模型
运行代码如下:
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
import mglearn
X,y=mglearn.datasets.load_extended_boston()
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)
ridge=Ridge(alpha=0.1).fit(X_train,y_train)
print("Training set score: {:.2f}".format(ridge.score(X_train,y_train)))
print("Test set score: {:.2f}".format(ridge.score(X_test,y_test)))输出:
Training set score: 0.93
Test set score: 0.77我们还可以通过coef_属性,来理解alpha参数是如何改变模型的。
- 更大的alpha意味着约束性更强的模型
我们来比较一下,运行代码如下:
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
import mglearn
from sklearn.linear_model import LinearRegression
X,y=mglearn.datasets.load_extended_boston()
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)
lr = LinearRegression().fit(X_train, y_train)
ridge=Ridge(alpha=1).fit(X_train,y_train)
ridge10=Ridge(alpha=10).fit(X_train,y_train)
ridge01=Ridge(alpha=0.1).fit(X_train,y_train)
plt.plot(ridge.coef_,'s',label="Ridge alpha=1")
plt.plot(ridge10.coef_,'^',label="Ridge alpha=10")
plt.plot(ridge.coef_,'v',label="Ridge alpha=0.1")
plt.plot(lr.coef_,'o',label="LinearRegression")
plt.xlabel("Coefficient index")
plt.ylabel("Coefficient magnitude")
plt.hlines(0,0,len(lr.coef_))
plt.ylim(-25,25)
plt.legend()
plt.show()效果图:

x轴对应coef_元素,对于alpha=10的模型,系数w大多在-3~+3之间;对于alpha=1的模型,系数w范围要大上一些;对于alpha=0.1的模型,系数范围更大。
4. Lasso
lasso也是约束系数将其接近于0,但是用到的方法不同,用到的是L1正则化
- L1正则化:是某些系数w刚好为0。也就是说某些特征被模型完全忽略。
我们将lasso应用到扩展的波士顿房价数据集上,运行代码如下:
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
import numpy as np
import mglearn
X,y=mglearn.datasets.load_extended_boston()
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)
lasso=Lasso().fit(X_train,y_train)
print("Training set score:{:.2f}".format(lasso.score(X_train,y_train)))
print("Test set score:{:.2f}".format(lasso.score(X_test,y_test)))
print("Number of features used: {}".format(np.sum(lasso.coef_ !=0)))输出:
Training set score:0.29
Test set score:0.21
Number of features used: 4我们可以从输出中看到,Lasso在训练集喝测试集上的表现都很差。这表示存在欠拟合。我们发现模型只用到了4个特征。Lasso也有正则化参数alpha,可以控制系数趋近于0的强度。默认值也为1.0
- 减小alpha,降低欠拟合,记住要同时增大max_iter的值(运行迭代最大次数)
运行代码如下:
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
import numpy as np
import mglearn
X,y=mglearn.datasets.load_extended_boston()
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)
lasso=Lasso(alpha=0.01).fit(X_train,y_train)
print("Training set score:{:.2f}".format(lasso.score(X_train,y_train)))
print("Test set score:{:.2f}".format(lasso.score(X_test,y_test)))
print("Number of features used: {}".format(np.sum(lasso.coef_ !=0)))输出:
Training set score:0.90
Test set score:0.77
Number of features used: 32从输出可以看出,alpha变小,我们可以拟合一个更复杂的模型。并且在训练集和数据集上的表现也更好。我们只用到特征中的32个
- 注意:如果把alpha的值设置的太小,那么就会消除正则化的效果,并出现过拟合,得到与LinearRegession相类似的结果
下面,我们看一下不同alpha值的lasso回归与岭回归的系数比较。
运行代码如下:
from sklearn.linear_model import Lasso
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge
import numpy as np
import mglearn
X,y=mglearn.datasets.load_extended_boston()
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)
ridge=Ridge(alpha=0.1).fit(X_train,y_train)
lasso=Lasso().fit(X_train,y_train)
lasso001=Lasso(alpha=0.01).fit(X_train,y_train)
lasso00001=Lasso(alpha=0.0001).fit(X_train,y_train)
plt.plot(lasso.coef_,'s',label="Lasso alpha=1")
plt.plot(lasso001.coef_,'^',label="Lasso alpha=0.01")
plt.plot(lasso00001.coef_,'v',label="Lasso alpha=0.0001")
plt.plot(ridge.coef_,'o',label="Ridge alpha=0.1")
plt.xlabel("Coefficient index")
plt.ylabel("Coefficient magnitude")
plt.hlines(0,0,len(ridge.coef_))
plt.ylim(-25,25)
#参数nocl设置图例中一行几个标签,loc参数设置位置
plt.legend(ncol=2,loc=(0,1.02))
plt.show()效果图:

根据图,我们可以看到在alpha=1的时候,不仅大部分系数w都是0,而且其他系数不为0的系数也很小;
alpha=0.01的时候,大部分特征为0;当alpha=0.0001的时候,我们得到正则化很弱的模型,大部分系数都不为0,并且很大。
图中圆形表示Ridge模型的最佳结果。可以看出,alpha=0.1的Ridge模型的预测性能与alpha=0.01的Lasso模型类似,但是Ridge模型里面所有系数都不为0。
今天就学到这儿了。
- 完整代码都在文章里面全部可以运行
- 后面的代码里面的注解省略了,前文都有注解
- 有不懂得地方和问题请留言
- 大家可以收藏一下以后学习用得到





















