HTML5频谱图 频谱图app

语谱图

语谱图（Spectrogram）是时序相关的傅里叶分析的显示图像，可以反映音乐信号频谱随时间改变而变换，语谱图的横坐标是时间，纵坐标是频率，坐标点值为语音数据能量。由于是采用二维平面表达三维信息，所以能量值的大小是通过颜色来表示的，颜色深，表示该点的语音能量越强。

语谱图中显示了大量与音乐信号特性相关的信息，如共振峰、能量等频域参数随时间的变化情况，它同时具有时域波形与频谱图的特点。也就是说，语谱图本身包含了音乐信号的所有的频谱信息，没有经过任何加工，所以语谱图关于音乐的信息是无损的。

语谱图中的花纹有横线，乱纹和竖直条等，横线是与时间轴平行的黑色带纹，它们是共振峰，从横线对应的频率和带宽可以确定相应的共振峰频率和带宽，在一段音频的语谱图中有没有横线出现是判断它是否是浊音的重要标志；竖直条是与时间轴垂直的窄黑条，每个竖直条相当于一个基音，条纹的起点相当于声纹脉冲的起点，条纹之间的距离表示基音，条纹越密表示基音频率越高

以许嵩最新单曲《雨幕》中10s~20s片段为例生成的语谱图如下：

生成图

（代码与生成结果）
MATLAB代码如下

% vv[Y参数1表示读取变量名，默认为WAV文件
%参数2表示读取模式，s表示默认归一化到±1
%参数3表示最大读取样例数，-1表示不限制
%参数4表示从起始点忽略的样例数，-1表示不忽略
读取到的结果：
%Y表示音频数据矩阵和声道
%FS表示采样频率
%WMODE用于输出
%FIDX为音频参数向量
[Y,FS,WMODE,FIDX]=readwav('03','s',-1,-1);
figure(1)
plot(Y)
title('double channel read')
Y1 = Y(:,1);        %Y为双声道数据
Y2 = Y(:,2);
figure(2)
suptitle('single channel read')
subplot(2,1,1)
plot(Y1);           %画波形图
hold on
subplot(2,1,2)
plot(Y2)
figure(3)
grid on;
specgram(Y1,128,8000,128,32);
title('long spectrogram')
figure(4)
grid on;
specgram(Y1,512,8000,512,128);
title('short spectrogram')

python代码如下：

import wave
import matplotlib.pyplot as plt
import numpy as np
import os

filename = '02.wav'
f = wave.open(filename,'rb')
# 得到语音参数
params = f.getparams()
nchannels, sampwidth, framerate,nframes = params[:4]
# 得到的数据是字符串，需要将其转成int型
strData = f.readframes(nframes)
wavaData = np.frombuffer(strData,dtype=np.int16)
# 归一化
wavaData = wavaData * 1.0/max(abs(wavaData))
# .T 表示转置
wavaData = np.reshape(wavaData,[nframes,nchannels]).T
f.close()
# 绘制频谱
plt.specgram(wavaData[0],Fs = framerate,scale_by_freq=True,sides='default')
plt.ylabel('Frequency')
plt.xlabel('Time(s)')
plt.show()

读图

直接读入的音频为双声道

窄带语谱图：

语音采样率为8000Hz,取窗长为512个数据点，帧移为窗长的1/4，即128个数据点。

窄带语谱图频率分辨率太过精细，不能很好体现出共振峰的大致位置，即反映不出基波的变化特性。宽带语谱图：

语音采样率为8000Hz,取窗长为128个数据点，帧移为窗长的1/4，即32个数据点。与窄带语谱图相反，宽带语谱图的时间分辨率很好，频率分辨率较低，不能很好反映声音的纹理特性，反映了频谱的时变特性，能很好分辨出共振峰的大致位置，但分辨不清谐波结构。

gabor滤波

Gabor变换属于加窗傅立叶变换，Gabor函数可以在频域不同尺度、不同方向上提取相关的特征。二维Gabor函数可以表示为：

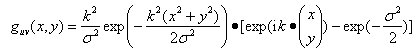
其中：

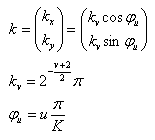
v的取值决定了Gabor滤波的波长，u的取值表示Gabor核函数的方向，K表示总的方向数。参数σ/k 决定了高斯窗口的大小，这里取 σ=√2π。程序中取4个频率（v=0, 1, …, 3），6个方向（即K=6，u＝0, 1, … ,5），共24个Gabor核函数。

python代码：

import cv2,os
import numpy as np
import matplotlib.pyplot as plt


def get_img(input_Path):
    img_paths = []
    for (path, dirs, files) in os.walk(input_Path):
        for filename in files:
            if filename.endswith(('.jpg','.png')):
                img_paths.append(path+'/'+filename)
    return img_paths


#构建Gabor滤波器
def build_filters():
     filters = []
     ksize = [7,9,11,13,15,17] # gabor尺度，6个
     lamda = np.pi/2.0         # 波长
     for theta in np.arange(0, np.pi, np.pi / 4): #gabor方向，0°，45°，90°，135°，共四个
         for K in range(6):
             kern = cv2.getGaborKernel((ksize[K], ksize[K]), 1.0, theta, lamda, 0.5, 0, ktype=cv2.CV_32F)
             kern /= 1.5*kern.sum()
             filters.append(kern)
     plt.figure(1)

     #用于绘制滤波器
     for temp in range(len(filters)):
         plt.subplot(4, 6, temp + 1)
         plt.imshow(filters[temp])
     plt.show()
     return filters

#Gabor特征提取
def getGabor(img,filters):
    res = [] #滤波结果
    for i in range(len(filters)):
        # res1 = process(img, filters[i])
        accum = np.zeros_like(img)
        for kern in filters[i]:
            fimg = cv2.filter2D(img, cv2.CV_8UC1, kern)
            accum = np.maximum(accum, fimg, accum)
        res.append(np.asarray(accum))

    #用于绘制滤波效果
    plt.figure(2)
    for temp in range(len(res)):
        plt.subplot(4,6,temp+1)
        plt.imshow(res[temp], cmap='gray' )
    plt.show()
    plt.savefig('./result.png')
    return res  #返回滤波结果,结果为24幅图，按照gabor角度排列


if __name__ == '__main__':
    input_Path = 'F:\programs\TSFL'
    filters = build_filters()
    img_paths = get_img(input_Path)
    for img in img_paths:
        img = cv2.imread(img)
        getGabor(img, filters)

展示

参考文章: python生成语谱图.

OpenCV—python Gabor滤波（提取图像纹理）.