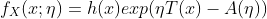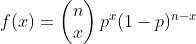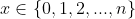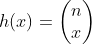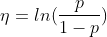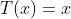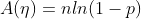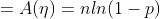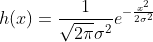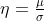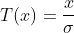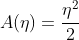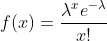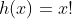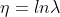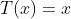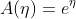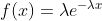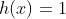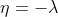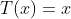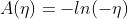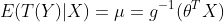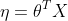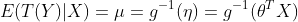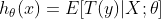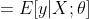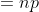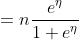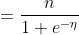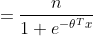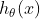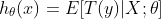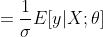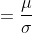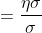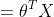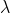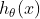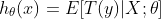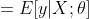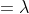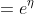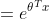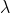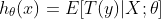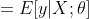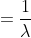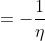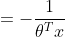python克朗巴哈系统 克朗巴哈系数

1.指数分布族

指数分布族（Exponential Family）是这样一组分布：这些分布的概率密度函数可以表示成以下形式：

其中，y是随机变量；h(x)称为基础度量值（base measure）；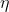

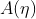
称为自然参数（natural parameter），也称为规范参数(canonical parameter)；T(x)称为充分统计量（sufficient statistic）；

则称为对数分割函数（log partition function）。

指数分布族包括了除了柯西分布和t分布以外的其他基本分布。

下面将几种常用概率分布的化为指数分布族的形式：

伯努利分布（Bernoulli Distribution）

伯努利分布的概率函数为：

       ，

因此，伯努利分布概率函数可以写成的指数分布函数的等价形式：

其中，

，

，

，

正态分布（Normal Distrbution）

正态分布的概率函数为：

其中：

，

，

，

泊松分布（Poisson Distribution）

泊松分布的概率函数为：

其中：

，

，

，

指数分布（Exponential Distribution）

，其中x>0

其中：

，

，

，

2.广义线性模型概念

如果目标变量Y服从指数分布族中某一特定分布，广义线性模型通过连接函数（link function），将重复统计量T(Y)的期望

和随机量X的线性组合建立相应的函数关系。即

其中，E(T(Y)|X)表示在X已知的前提下，重复统计量T(Y)的期望值，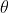

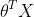
为线性组合的系数，

为线性指示器（linear predictor），g(x)为连接函数。

3.广义线性模型构建

机器学习中广义线性模型的构建是为了通过训练样本来预测y的值。

1)判断在X给定的情况下，Y服从指数分布族中的何种分布；

2)

3) 通过连接函数建立X与充分统计量T(Y)之间的函数关系：

下面以常用的分布为例，构建广义线性模型：

伯努利分布

假设在X给定的情况下，Y服从伯努利分布，Y|X~B(n,p)，那么预测函数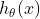

的表达式推导如下：

                                                                               

                                                                               

                                                                               

                                                                                

当n=1时，伯努利分布转化成二项分布，仅有｛0、1｝二值，

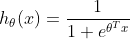
，为Logistic回归。

正态分布

假设在X给定的情况下，Y服从期望为方差为的正态分布，即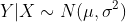

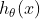
，那么预测函数

的表达式推导如下：

那么预测函数

的表达式推导如下：

                                                                               

                                                                               

                                                                               

                                                                               

这正是大家熟悉的一般线性回归方程。

泊松分布

假设在X给定的情况下，Y服从泊松分布，Y|X~P(

)

预测函数

的表达式推导如下：

指数分布

假设在X给定的情况下，Y服从指数分布，Y|X~e(

)

预测函数

的表达式推导如下：