1、梯度下降法
假设:
- x:输入特征
- y:样本标签,实际输出
- (x,y):训练样本
- m表示训练样本总数,loop:i
- n表示特征总数,loop:j
目的是通过对训练样本进行学习,构造一个模型,使得能够对任意的输入进行预测。
获得合适的参数,使得h(x)与y之间的差距最小,即求损失函数的最小值。
线性方程:
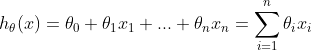
损失函数:

梯度递减函数:
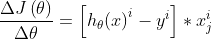
参数更新函数:
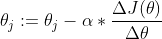
其中,

是learningRate,可以根据经验取值{0.01,0.03,0.1,0.3,1,1.3}等,也可以根据自己的情况,多次训练,取收敛最快的。
随着收敛越来越接近,梯度也会越来越小;选取的初始下降位置不同,收敛的位置就不一样。
2、正规方程
输入样本可表示为:
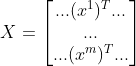
样本标签表示为:
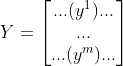
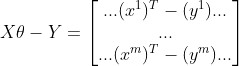
由

可得损失函数:
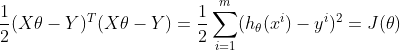
必须使得损失函数有最小值,同上,须求得损失函数有的最小值时的参数,因此可求
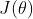
关于
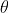
的导数,得
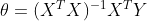
3、局部加权回归
与梯度下降不同的是,损失函数加入权重,使得靠近X的点增加权证,而远离的减少权重(降低贡献率)。损失函数:
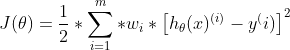

其中
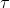
决定权重的下降速率,若

,则区域是瘦高型的,若它大,则为庞宽型。若
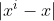
is samll, 则
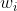
=1若
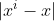
is large, 则
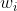
=0
4 代码实现
数据使用的都是Stanford公开课提供的数据,参考文献种有链接。代码一和代码二都是实现二维数据的回归预测。数据包含50个2-8岁的儿童的身高数据,并对3.5到7岁的身高进行预测。
代码一:正规方程实现
clear all; clc;
data=xlsread('E:\MATLAB\Workspace\data\student.xls');
x=data(:,3);
y=data(:,4)
plot(x,y,'*');
xlabel('height:cm');
ylabel('weight:kg');
x=[ones(size(x,1),1),x];
w=inv(x'*x)*x'*y % w计算回归线的斜率和截距,w(1)是截距,
hold on
plot(x(:,2),w(2)*x(:,2)+w(1));代码二:梯度下降
clear all; clc;
% data=xlsread('E:\MATLAB\Workspace\data\student.xls');
% x=data(:,3);
% y=data(:,4)
x=load('E:\MATLAB\Workspace\data\ex2x.dat');
y=load('E:\MATLAB\Workspace\data\ex2y.dat');
plot(x,y,'*');
xlabel('height:cm');
ylabel('weight:kg');
%% gradient descend
m=length(x);
x=[ones(m,1),x];
theta=zeros(size(x(1,:)))'; % initilize the fitting parameter,本次使用二维数据,
alpha=0.07;
max_iter=1500;
for i=1:max_iter
grad=1/m.*x'*(x*theta-y);
theta=theta-alpha.*grad;
end
%% plot the linear fit
hold on;
plot(x(:,2),x*theta,'-');
legend('Training data','linear regression');
hold off;
%% prediction;
extra_theta=(x'*x)\x'*y;
predict1=[1,3.5]*theta;
predict2=[1,7]*theta;
%% calculate J
theta0_vals=linspace(-3,3,100);%是给出-3到3之间的100个数,均匀的选取,即线性的选取。
theta1_vals=linspace(-1,1,100);
J_vals=zeros(length(theta0_vals),length(theta1_vals));
for i=1:length(theta0_vals)
for j=1:length(theta1_vals)
t=[theta0_vals(i);theta1_vals(j)];
J_vals(i,j)=(0.5*m).*(x*t-y)'*(x*t-y);%cost function
end
end
% Because of the way meshgrids work in the surf command, we need to
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals';
% Surface plot
figure;
surf(theta0_vals,theta1_vals,J_vals);
xlabel('\theta_0');ylabel('\theta_1');%斜杠 转义字符
% 等高线;
% 指的是在10^(-4)到10^(4)之间选取15个数,这些数按照指数大小来选取,
% 即指数部分是均匀选取的,但是由于都取了10为底的指数,所以最终是服从指数分布选取的。
figure;
contour(theta0_vals,theta1_vals,J_vals,logspace(-4,4,15));
xlabel('\theta_0');ylabel('\theta_1');实验截图:
训练样本和回归曲线预测图:

损失函数和参数之间的曲面图:

损失函数等高线图:

代码三:(数据:47个训练样本,y为房子的价格,x有两个属性,一个是房子的大小,另一个是房子卧室的个数。需要通过这些训练数据学习函数,预测已知房子大小和确定卧室数目的房子的价格)。在这个例子中,有对learningRate的选择,通过观察损失函数和迭代次数之间的函数曲线,选择收敛速度最快的learningRate。
clear all;clc;
x=load('E:\MATLAB\Workspace\data\ex3x.dat');
y=load('E:\MATLAB\Workspace\data\ex3y.dat');
m=length(x);
x=[ones(m,1),x]
meanx=mean(x);
stdx=std(x);
%标准化数据
x(:,2)=bsxfun(@rdivide,bsxfun(@minus,x(:,2),meanx(2)),stdx(2));
x(:,3)=bsxfun(@rdivide,bsxfun(@minus,x(:,3),meanx(3)),stdx(3));
%初始化alpha
alpha=[0.01,0.03,0.1,0.3,1,1.3];
plotstyle={'r','g','b','y','k','m'};
num_iter=100;%尝试迭代的次数
m=size(x,1);%训练样本的次数
for i=1:length(alpha)
theta=zeros(size(x,2),1);
jtheta=zeros(num_iter,1);
for j=1:num_iter
jtheta(j)=(0.5*m).*(x*theta-y)'*(x*theta-y);
grad=1/m.*x'*(x*theta-y);
theta=theta-alpha(i).*grad;
end
plot(jtheta,char(plotstyle(i)),'LineWidth', 1)%此处一定要通过char函数来转换
hold on
if(1==alpha(i))
theta_grad=theta;
end
end
legend('0.01','0.03','0.1','0.3','1','1.3');
xlabel('number of iter');
ylabel('cost function');
%% prediction function
price_grad=theta_grad'*[1 (1650-meanx(2))/stdx(2) (3-meanx(3)/stdx(3))]'
%% normal equation
theta_norm=inv((x'*x))*x'*y;
price_norm=theta_norm'*[1 (1650-meanx(2))/stdx(2) (3-meanx(3)/stdx(3))]';实验截图:
learningRate侧视图:

由图可知,当learningRate=1时,收敛最快。另外,假如设置learningRate=1.4,则得到以下结果,因为学习因子实际上定义的你的邻域范围(或者精确地说,是邻域点集的直径),如果learningRate太大,就会使得训练发散。
learningRate过大测试图:






















