tslearn 时间序列KShape python

时间序列预测

• 什么是时间序列
• 线性回归预测

• time-step特征
• lag特征
• 案例

• 导入数据
• 时间步长特征预测模型
• 滞后特征预测模型

• 时间序列特征

• 1. 趋势

• 趋势的特征工程
• 案例

• 2. 季节性

• 季节指示器
• 傅里叶特征

• 案例

• 3. 周期

• 自相关性
• 选择阶数
• 案例

本文是最近在kaggle上学习的时间序列预测的笔记。觉得课程上讲得很有用，就整理成笔记啦。

什么是时间序列

这里有一个时间序列的数据——hardcover 书籍销售量(30天的销量)，这里有一个时间索引Date。

import pandas as pd

df = pd.read_csv(
    "./data/book_sales.csv",
    index_col='Date',
    parse_dates=['Date'],
).drop('Paperback', axis=1)

df.head()

线性回归预测

对于时间序列的两个特征：时间步长time-step特征和滞后lag特征，建立两个特征的线性回归：

$target = weight_1 * feature_1 + weight_2 * feature_2 + bias$

一般用最小二乘法估计参数$𝑤𝑒𝑖𝑔ℎ𝑡_1,𝑤𝑒𝑖𝑔ℎ𝑡_2$且称为回归系数，其中，bias也称为截距。

time-step特征

最基础的time-step特征就是time dummy时间虚拟变量，如下表的Time特征就是计算的时间步长特征。

import numpy as np

df['Time'] = np.arange(len(df.index))

df.head()

用时间步长特征预测因变量的线性回归模型为：

$target = weight * time + bias$

import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use("seaborn-whitegrid")
plt.rc(
    "figure",
    autolayout=True,
    figsize=(11, 4),
    titlesize=18,
    titleweight='bold',
)
plt.rc(
    "axes",
    labelweight="bold",
    labelsize="large",
    titleweight="bold",
    titlesize=16,
    titlepad=10,
)
%config InlineBackend.figure_format = 'retina'

fig, ax = plt.subplots()
ax.plot('Time', 'Hardcover', data=df, color='0.75')
ax = sns.regplot(x='Time', y='Hardcover', data=df, ci=None, scatter_kws=dict(color='0.25'))
ax.set_title('Time Plot of Hardcover Sales')

这个简单的线性模型，使用时间虚拟变量去预测因变量，但是从图可见预测效果一般。

lag特征

滞后特征关注的是因变量的转换，比如说将因变量全部上移或者下移一步/几步。简单举例，这里把因变量下移一步，得到一个Lag_11阶滞后变量。在Python中可以通过shift方法轻松实现：

df['Lag_1'] = df['Hardcover'].shift(1)
df = df.reindex(columns=['Hardcover', 'Lag_1'])

df.head()

用滞后特征预测因变量的线性回归模型为：

$target = weight * lag + bias$

可以通过散点图看看因变量与其滞后变量之间的关系，如下图：

fig, ax = plt.subplots()
ax = sns.regplot(x='Lag_1', y='Hardcover', data=df, ci=None, scatter_kws=dict(color='0.25'))
ax.set_aspect('equal')
ax.set_title('Lag Plot of Hardcover Sales')

从图中可以看出，因变量Hardcover和其滞后变量有关，且随着1阶滞后变量增加，因变量也随之增加，即今天的高销量意味着明天的高销量。

案例

Tunnel Traffic是一个关于瑞士的Baregg Tunnel 车辆旅行的日数据，时间是从2003年11月1号到2005年11月16号。

导入数据

注意日期格式数据，必须变成时间戳Timestamp才能进行数据分析和拟合模型。

tunnel = pd.read_csv("./data/tunnel.csv", parse_dates=["Day"])

tunnel = tunnel.set_index("Day")
tunnel = tunnel.to_period()

tunnel.tail()

时间步长特征预测模型

在这里的数据没有缺失值，故用下列方法计算时间虚拟变量time dummy。

df = tunnel.copy()

df['Time'] = np.arange(len(tunnel.index))

df.head()

直接用scikit-learn中的LinearRegression来拟合模型。

from sklearn.linear_model import LinearRegression

X = df.loc[:, ['Time']]  # 特征features
y = df.loc[:, 'NumVehicles']  # 因变量target

# 拟合模型
model = LinearRegression()
model.fit(X, y)

# 预测模型
y_pred = pd.Series(model.predict(X), index=X.index)

# 预测结果可视化
ax = y.plot(**plot_params)
ax = y_pred.plot(ax=ax, linewidth=3)
ax.set_title('Time Plot of Tunnel Traffic')

滞后特征预测模型

先用Python的shift方法计算滞后特征。

df['Lag_1'] = df['NumVehicles'].shift(1)
df.head()

这里对于缺失值的处理，我们直接删掉了。

from sklearn.linear_model import LinearRegression

X = df.loc[:, ['Lag_1']]# 特征
X.dropna(inplace=True)  
y = df.loc[:, 'NumVehicles']  # 因变量
y, X = y.align(X, join='inner')  # 确保特征和因变量一一对应drop corresponding values in target

model = LinearRegression()
model.fit(X, y)

y_pred = pd.Series(model.predict(X), index=X.index)

用散点图分析滞后特征和因变量之间的关系，即今天的数据和前一天数据的关系。

fig, ax = plt.subplots()
ax.plot(X['Lag_1'], y, '.', color='0.25')
ax.plot(X['Lag_1'], y_pred)
ax.set_aspect('equal')
ax.set_ylabel('NumVehicles')
ax.set_xlabel('Lag_1')
ax.set_title('Lag Plot of Tunnel Traffic')

接下来看看预测的结果：

ax = y.plot(**plot_params)
ax = y_pred.plot()

时间序列特征

有时候线性回归模型预测不太理想，接下来讲讲述时间序列的特征，以及其他的预测模型。

1. 趋势

趋势trend就是时间序列的长期走势，下图是4种时间序列趋势。

在这里关注的是平均趋势，接下来介绍移动平均Moving Average，目的是平滑或者过滤掉任何短期波动，只保留长期变化。

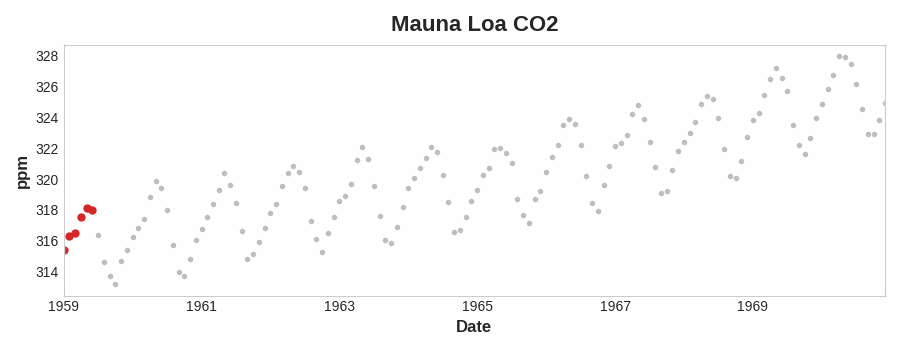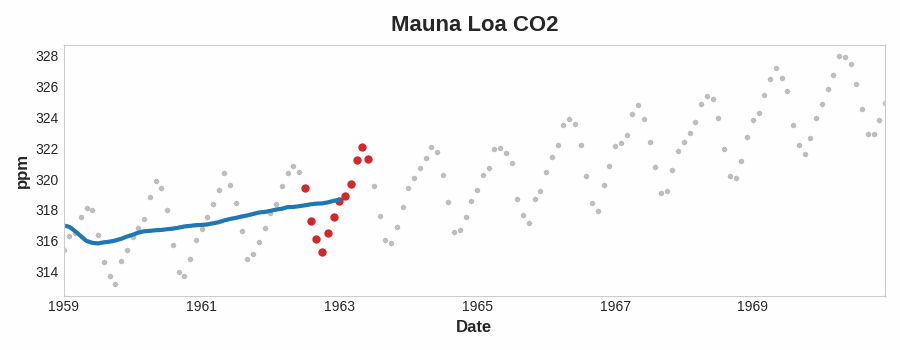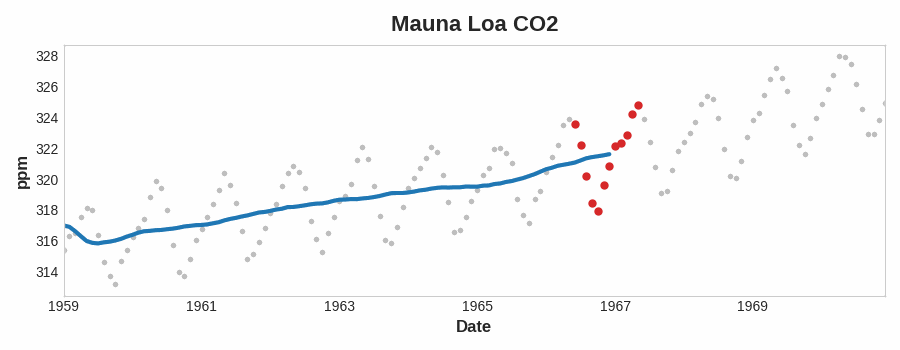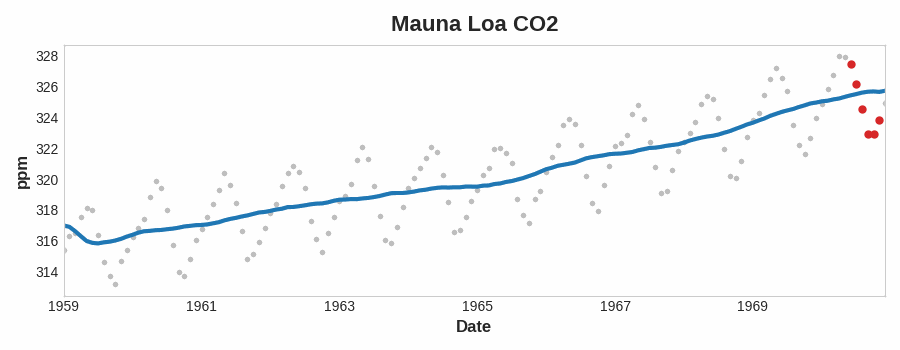
这里可以看到一个明显的线性趋势，每一个蓝色曲线的点是12个红色点的平均，也平滑了时间序列的季节性。

趋势的特征工程

• 线性趋势

$target = a * time + b$

• 二次趋势

$target = a * time^2 + b * time + c$

如下图，有弧形的可以用二次或者更高次预测。

这两种模型都可以用scikit-learn的LinearRegression来实现。

案例

也是用上面的Tunnel Traffic数据集。

tunnel = pd.read_csv("./data/tunnel.csv", parse_dates=["Day"])
tunnel = tunnel.set_index("Day").to_period()

数据集是日数据集，所以用365天窗口平滑，去平滑短期的波动。在Python中用rolling方法去计算移动平均。

moving_average = tunnel.rolling(
    window=365,       # 365-day window
    center=True,      # puts the average at the center of the window
    min_periods=183,  # 值为窗口值的一半choose about half the window size
).mean()              # compute the mean (could also do median, std, min, max, ...)

ax = tunnel.plot(style=".", color="0.5")
moving_average.plot(
    ax=ax, linewidth=3, title="Tunnel Traffic - 365-Day Moving Average", legend=False,
)

从上图，我们可以看到线性趋势。从statsmodels.tsa.deterministic中导入eterministicProcess，其中参数order：1是线性，2是二次，3是三次，等等。

from statsmodels.tsa.deterministic import DeterministicProcess

dp = DeterministicProcess(
    index=tunnel.index,  # dates from the training data
    constant=True,       # dummy feature for the bias (y_intercept)
    order=1,             # the time dummy (trend)
    drop=True,           # drop terms if necessary to avoid collinearity共线性
)
# `in_sample` creates features for the dates given in the `index` argument
X = dp.in_sample()

X.head()

这里trend从1到747，const=1。

接下来拟合模型：

from sklearn.linear_model import LinearRegression

y = tunnel["NumVehicles"]  # 因变量the target

model = LinearRegression(fit_intercept=False)
model.fit(X, y)

y_pred = pd.Series(model.predict(X), index=X.index)

# 可视化预测结果
ax = tunnel.plot(style=".", color="0.5", title="Tunnel Traffic - Linear Trend")
_ = y_pred.plot(ax=ax, linewidth=3, label="Trend")

从下图结果可见，线性回归LinearRegression模型和上面的移动平均相似，所以这里用线性趋势是合适的。

接下来进行一个30天的预测：

X = dp.out_of_sample(steps=30)

y_fore = pd.Series(model.predict(X), index=X.index)# 进行30天的预测

# 可视化结果
ax = tunnel["2005-05":].plot(title="Tunnel Traffic - Linear Trend Forecast", **plot_params)
ax = y_pred["2005-05":].plot(ax=ax, linewidth=3, label="Trend")
ax = y_fore.plot(ax=ax, linewidth=3, label="Trend Forecast", color="C3")
_ = ax.legend()

上图中红色部分就是30天的预测结果。

2. 季节性

季节性可能与自然界的周期有关，比如说周，天，年；也可能和社会习俗，节假日等有关。

以下是4种季节性图形。

我们将介绍两种季节特征：

• 指示器indicators
  一般用于分析较少数据时，比如日观测数据的周季节性
• 傅里叶特征Fourier
  一般用于分析大量数据时，比如日观测数据的年季节性

下图是一周数据的季节性周期。可以看到：工作日数据更高，周末下降

季节指示器

季节指示器是表示时间序列水平的季节性差异的二元特征，一般通过one-hot encoding方法得到季节指示器，如下图我们得到周季节指示器，注意：这里只有6个新的虚拟变量dummy特征(删除一个季节指示器后线性回归更有效)。

傅里叶特征

我们讨论的傅里叶特征更适合于长期季节性，比如下图所示的年季节性：可以看到这一年有三次长的上升和下降的趋势，如果是周季节模式，有52周。

傅里叶特征的一般处理方法是：sine和cosine函数，数据的变化频率可能有：一年一次，一年2次，一年3次等。

上图中上方的图频率是一年1次，下面是一年2次。

下图是4个傅里叶特征来拟合年季节性。图中下面黑色曲线是这4种曲线加总去近似季节性周期。

那么我们应该选择几条傅里叶路径去拟合呢？可以从周期图来选择，从下图来看：周期图在季度之后开始下降，所以频率为一年4次，即选择4条傅里叶路径去模拟年季节性，后面的周频率可以忽略，因为它更适合用上节的季节指示器。

下面的代码是傅里叶特征的计算方法：

import numpy as np


def fourier_features(index, freq, order):
    time = np.arange(len(index), dtype=np.float32)
    k = 2 * np.pi * (1 / freq) * time
    features = {}
    for i in range(1, order + 1):
        features.update({
            f"sin_{freq}_{i}": np.sin(i * k),
            f"cos_{freq}_{i}": np.cos(i * k),
        })
    return pd.DataFrame(features, index=index)
fourier_features(y, freq=365.25, order=4)

案例

仍然使用Tunnel Traffic数据集，下面主要代码定义了两个函数：seasonal_plot()和plot_periodogram。

from pathlib import Path
from warnings import simplefilter

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn.linear_model import LinearRegression
from statsmodels.tsa.deterministic import CalendarFourier, DeterministicProcess

simplefilter("ignore")

# Set Matplotlib defaults
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True, figsize=(11, 5))
plt.rc(
    "axes",
    labelweight="bold",
    labelsize="large",
    titleweight="bold",
    titlesize=16,
    titlepad=10,
)
plot_params = dict(
    color="0.75",
    style=".-",
    markeredgecolor="0.25",
    markerfacecolor="0.25",
    legend=False,
)
%config InlineBackend.figure_format = 'retina'


# annotations: https://stackoverflow.com/a/49238256/5769929
def seasonal_plot(X, y, period, freq, ax=None):
    if ax is None:
        _, ax = plt.subplots()
    palette = sns.color_palette("husl", n_colors=X[period].nunique(),)
    ax = sns.lineplot(
        x=freq,
        y=y,
        hue=period,
        data=X,
        ci=False,
        ax=ax,
        palette=palette,
        legend=False,
    )
    ax.set_title(f"Seasonal Plot ({period}/{freq})")
    for line, name in zip(ax.lines, X[period].unique()):
        y_ = line.get_ydata()[-1]
        ax.annotate(
            name,
            xy=(1, y_),
            xytext=(6, 0),
            color=line.get_color(),
            xycoords=ax.get_yaxis_transform(),
            textcoords="offset points",
            size=14,
            va="center",
        )
    return ax


def plot_periodogram(ts, detrend='linear', ax=None):
    from scipy.signal import periodogram
    fs = pd.Timedelta("1Y") / pd.Timedelta("1D")
    freqencies, spectrum = periodogram(
        ts,
        fs=fs,
        detrend=detrend,
        window="boxcar",
        scaling='spectrum',
    )
    if ax is None:
        _, ax = plt.subplots()
    ax.step(freqencies, spectrum, color="purple")
    ax.set_xscale("log")
    ax.set_xticks([1, 2, 4, 6, 12, 26, 52, 104])
    ax.set_xticklabels(
        [
            "Annual (1)",
            "Semiannual (2)",
            "Quarterly (4)",
            "Bimonthly (6)",
            "Monthly (12)",
            "Biweekly (26)",
            "Weekly (52)",
            "Semiweekly (104)",
        ],
        rotation=30,
    )
    ax.ticklabel_format(axis="y", style="sci", scilimits=(0, 0))
    ax.set_ylabel("Variance")
    ax.set_title("Periodogram")
    return ax

tunnel = pd.read_csv("./data/tunnel.csv", parse_dates=["Day"])
tunnel = tunnel.set_index("Day").to_period("D")

下面两个图分别是周季节性和年季节性。

X = tunnel.copy()

# days within a week
X["day"] = X.index.dayofweek  # the x-axis (freq)
X["week"] = X.index.week  # the seasonal period (period)

# days within a year
X["dayofyear"] = X.index.dayofyear
X["year"] = X.index.year
fig, (ax0, ax1) = plt.subplots(2, 1, figsize=(11, 6))
seasonal_plot(X, y="NumVehicles", period="week", freq="day", ax=ax0)
seasonal_plot(X, y="NumVehicles", period="year", freq="dayofyear", ax=ax1)

从下面的周期图来分析，有强的周季节性，相对弱的年季节性，图中下降大约在Bimonthly (6)和Monthly (12)之间，这里我们现在10条傅里叶路径。

这里我们使用DeterministicProcess来同时实现周季节性和年季节性。

from statsmodels.tsa.deterministic import CalendarFourier, DeterministicProcess

fourier = CalendarFourier(freq="A", order=10)  # 10 sin/cos pairs for "A"nnual seasonality

dp = DeterministicProcess(
    index=tunnel.index,
    constant=True,               # dummy feature for bias (y-intercept)
    order=1,                     # 线性趋势trend (order 1 means linear)
    seasonal=True,               # 季节指示器weekly seasonality (indicators)
    additional_terms=[fourier],  # 傅里叶特征annual seasonality (fourier)
    drop=True,                   # 避免共线性drop terms to avoid collinearity
)

X = dp.in_sample()  # create features for dates in tunnel.index

处理好特征之后，就可以去拟合模型和预测结果了，下面是90天预测结果。

y = tunnel["NumVehicles"]

model = LinearRegression(fit_intercept=False)
_ = model.fit(X, y)

y_pred = pd.Series(model.predict(X), index=y.index)
X_fore = dp.out_of_sample(steps=90)
y_fore = pd.Series(model.predict(X_fore), index=X_fore.index)

ax = y.plot(color='0.25', style='.', title="Tunnel Traffic - Seasonal Forecast")
ax = y_pred.plot(ax=ax, label="Seasonal")
ax = y_fore.plot(ax=ax, label="Seasonal Forecast", color='C3')
_ = ax.legend()

3. 周期

周期就是一个时间序列表现的上升或者下降的趋势，这个时间序列当期的值依靠之前期的值，但不一定依赖时间步长。周期是序列依赖的一种情况。经济，传染病，人口，火山爆发，类似自然现象通常有周期行为。

一般情况下，周期行为比季节性更没有规律/不规则。

下面数据$y$是美国的月失业率。

import pandas as pd

# Federal Reserve dataset: https://www.kaggle.com/federalreserve/interest-rates
reserve = pd.read_csv(
    "./data/reserve.csv",
    parse_dates={'Date': ['Year', 'Month', 'Day']},
    index_col='Date',
)

y = reserve.loc[:, 'Unemployment Rate'].dropna().to_period('M')
df = pd.DataFrame({
    'y': y,
    'y_lag_1': y.shift(1),
    'y_lag_2': y.shift(2),    
})

df.head()

自相关性

为了预测失业率，用前两期失业率y_lag_1，y_lag_2做特征来预测。下图表示前4个滞后变量与因变量都有强的线性关系，也称为自相关性。

选择阶数

比如上图，如果滞后2阶没有更新的信息，我们选择滞后1阶就可以了，因为滞后2阶是1阶的上1阶。

偏自相关图可以帮助选择滞后阶数。下面的偏自相关图，滞后1到6阶都是在蓝色区域外面(蓝色区域在95%的置信水平表示无关)，因此可以选择滞后1到6阶作为特征来预测美国的失业率。

注意：自相关和偏自相关表示的是线性依赖关系。对于非线性关系的，要么转化形式使得具有线性关系，要么用其他算法拟合。

案例

数据集Flu Trends是2009年到2016年每周医生看的感冒病例记录，有129个列。目的是预测下一周的感冒病例的数量。

首先看一下因变量的历史数据变化趋势：

from pathlib import Path
from warnings import simplefilter

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from scipy.signal import periodogram
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from statsmodels.graphics.tsaplots import plot_pacf

simplefilter("ignore")

# Set Matplotlib defaults
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True, figsize=(11, 4))
plt.rc(
    "axes",
    labelweight="bold",
    labelsize="large",
    titleweight="bold",
    titlesize=16,
    titlepad=10,
)
plot_params = dict(
    color="0.75",
    style=".-",
    markeredgecolor="0.25",
    markerfacecolor="0.25",
)
%config InlineBackend.figure_format = 'retina'


def lagplot(x, y=None, lag=1, standardize=False, ax=None, **kwargs):
    from matplotlib.offsetbox import AnchoredText
    x_ = x.shift(lag)
    if standardize:
        x_ = (x_ - x_.mean()) / x_.std()
    if y is not None:
        y_ = (y - y.mean()) / y.std() if standardize else y
    else:
        y_ = x
    corr = y_.corr(x_)
    if ax is None:
        fig, ax = plt.subplots()
    scatter_kws = dict(
        alpha=0.75,
        s=3,
    )
    line_kws = dict(color='C3', )
    ax = sns.regplot(x=x_,
                     y=y_,
                     scatter_kws=scatter_kws,
                     line_kws=line_kws,
                     lowess=True,
                     ax=ax,
                     **kwargs)
    at = AnchoredText(
        f"{corr:.2f}",
        prop=dict(size="large"),
        frameon=True,
        loc="upper left",
    )
    at.patch.set_boxstyle("square, pad=0.0")
    ax.add_artist(at)
    ax.set(title=f"Lag {lag}", xlabel=x_.name, ylabel=y_.name)
    return ax


def plot_lags(x, y=None, lags=6, nrows=1, lagplot_kwargs={}, **kwargs):
    import math
    kwargs.setdefault('nrows', nrows)
    kwargs.setdefault('ncols', math.ceil(lags / nrows))
    kwargs.setdefault('figsize', (kwargs['ncols'] * 2, nrows * 2 + 0.5))
    fig, axs = plt.subplots(sharex=True, sharey=True, squeeze=False, **kwargs)
    for ax, k in zip(fig.get_axes(), range(kwargs['nrows'] * kwargs['ncols'])):
        if k + 1 <= lags:
            ax = lagplot(x, y, lag=k + 1, ax=ax, **lagplot_kwargs)
            ax.set_title(f"Lag {k + 1}", fontdict=dict(fontsize=14))
            ax.set(xlabel="", ylabel="")
        else:
            ax.axis('off')
    plt.setp(axs[-1, :], xlabel=x.name)
    plt.setp(axs[:, 0], ylabel=y.name if y is not None else x.name)
    fig.tight_layout(w_pad=0.1, h_pad=0.1)
    return fig


#data_dir = Path("../input/ts-course-data")
flu_trends = pd.read_csv("./data/flu-trends.csv")
flu_trends.set_index(
    pd.PeriodIndex(flu_trends.Week, freq="W"),
    inplace=True,
)
flu_trends.drop("Week", axis=1, inplace=True)

ax = flu_trends.FluVisits.plot(title='Flu Trends', **plot_params)
_ = ax.set(ylabel="Office Visits")

从上图可以看到不规则的周期，而不是明显的季节性：峰值往往出现在新年的时候，有时候年前有时候年后，峰值有时候大，有时候小些。

接下来看一下滞后变量与因变量之间的关系，和偏自相关图：

_ = plot_lags(flu_trends.FluVisits, lags=12, nrows=2)
_ = plot_pacf(flu_trends.FluVisits, lags=12)

图中部分滞后变量与因变量有线性关系。

偏自相关图中表明阶数可以选择1,2,3,4阶。本例中的缺失值用0填充：

def make_lags(ts, lags):
    return pd.concat(
        {
            f'y_lag_{i}': ts.shift(i)
            for i in range(1, lags + 1)
        },
        axis=1)


X = make_lags(flu_trends.FluVisits, lags=4)
X = X.fillna(0.0)

# Create target series and data splits
y = flu_trends.FluVisits.copy()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=60, shuffle=False)

# 拟合和预测Fit and predict
model = LinearRegression()  # `fit_intercept=True` since we didn't use DeterministicProcess
model.fit(X_train, y_train)
y_pred = pd.Series(model.predict(X_train), index=y_train.index)
y_fore = pd.Series(model.predict(X_test), index=y_test.index)

# 可视化
ax = y_train.plot(**plot_params)
ax = y_test.plot(**plot_params)
ax = y_pred.plot(ax=ax)
_ = y_fore.plot(ax=ax, color='C3')

只展示后面预测部分：

ax = y_test.plot(**plot_params)
_ = y_fore.plot(ax=ax, color='C3')

对于预测的结果还可以做优化，我们只用了因变量滞后特征做预测，如果加了其他特征的滞后变量是不是会效果更好呢！

下图是FluCough和因变量FluVisits的时序图。现在几个变量作为特征值，再对这些特征进行滞后1,2,3阶处理，因变量阶数同上1,2,3,4阶，缺失值也是用0填充。

search_terms = ["FluContagious", "FluCough", "FluFever", "InfluenzaA", "TreatFlu", "IHaveTheFlu", "OverTheCounterFlu", "HowLongFlu"]

# Create three lags for each search term
X0 = make_lags(flu_trends[search_terms], lags=3)

# Create four lags for the target, as before
X1 = make_lags(flu_trends['FluVisits'], lags=4)

# Combine to create the training data
X = pd.concat([X0, X1], axis=1).fillna(0.0)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=60, shuffle=False)

model = LinearRegression()
model.fit(X_train, y_train)
y_pred = pd.Series(model.predict(X_train), index=y_train.index)
y_fore = pd.Series(model.predict(X_test), index=y_test.index)

ax = y_test.plot(**plot_params)
_ = y_fore.plot(ax=ax, color='C3')

对于时间序列的周期性，没有明显的趋势或季节性。