目录
差分指数平滑法
一阶差分指数平滑法
二阶差分指数平滑模型
自适应滤波法
自适应滤波法的基本过程
N, k 值和初始权数的确定
差分指数平滑法
在上节我们已经讲过,当时间序列的变动具有直线趋势时,用一次指数平滑法会出现滞后偏差,其原因在于数据不满足模型要求。因此,我们也可以从数据变换的角度来考虑改进措施,即在运用指数平滑法以前先对数据作一些技术上的处理,使之能适合于 一次指数平滑模型,以后再对输出结果作技术上的返回处理,使之恢复为原变量的形态。 差分方法是改变数据变动趋势的简易方法。下面我们讨论如何用差分方法来改进指数平 滑法。
一阶差分指数平滑法

在前面我们已分析过,指数平滑值实际上是一种加权平均数。因此把序列中逐期增 量的加权平均数(指数平滑值)加上当前值的实际数进行预测,比一次指数平滑法只用 变量以往取值的加权平均数作为下一期的预测更合理。从而使预测值始终围绕实际值上 下波动,从根本上解决了在有直线增长趋势的情况下,用一次指数平滑法所得出的结果 始终落后于实际值的问题。
例 7 某工业企业 1977~1986 年锅炉燃料消耗量资料如表 8 所示,试预测 1987 年 的燃料消耗量。

解 由资料可以看出,燃料消耗量,除个别年份外,逐期增长量大体在 200 吨左右,即呈直线增长,因此可用一阶差分指数平滑模型来预测。我们取 α = 0.4,初始值为新序列首项值,计算结果列于表 8 中。预测 1987 年燃料消耗量为
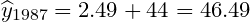
( 百吨 )
二阶差分指数平滑模型

差分方法和指数平滑法的联合运用,除了能克服一次指数平滑法的滞后偏差之外, 对初始值的问题也有显著的改进。因为数据经过差分处理后,所产生的新序列基本上是平稳的。这时,初始值取新序列的第一期数据对于未来预测值不会有多大影响。其次, 它拓展了指数平滑法的适用范围,使一些原来需要运用配合直线趋势模型处理的情况可用这种组合模型来取代。但是,于指数平滑法存在的加权系数 α 的选择问题,以及只能逐期预测问题,差分指数平滑模型也没有改进。
自适应滤波法
自适应滤波法的基本过程
自适应滤波法与移动平均法、指数平滑法一样,也是以时间序列的历史观测值进行 某种加权平均来预测的,它要寻找一组“佳”的权数,其办法是先用一组给定的权数 来计算一个预测值,然后计算预测误差,再根据预测误差调整权数以减少误差。这样反 复进行,直至找出一组“佳”权数,使误差减少到低限度。由于这种调整权数的过 程与通讯工程中的传输噪声过滤过程极为接近,故称为自适应滤波法。

下面举一个简单的例子来说明此法的全过程。设有一个时间序列包括 10 个观测值, 如表 9 所示。试用自适应滤波法,以两个权数来求第 11 期的预测值。


在实际应用中,权数调整计算工作量可能很大,必须借助于计算机才能实现。
计算的 MATLAB 程序如下:
clc,clear
yt=0.1:0.1:1;
m=length(yt);
k=0.9; N=2; Terr=10000;
w=ones(1,N)/N;
while abs(Terr)>0.00001
Terr=[];
for j=N+1:m-1
yhat(j)=w*yt(j-1:-1:j-N)';
err=yt(j)-yhat(j);
Terr=[Terr,abs(err)];
w=w+2*k*err*yt(j-1:-1:j-N);
end
Terr=max(Terr);
end
w, yhatN, k 值和初始权数的确定
在开始调整权数时,首先要确定权数个数 N 和学习常数k 。一般说来,当时间序 列的观测值呈季节变动时, N 应取季节性长度值。如序列以一年为周期进行季节变动 时,若数据是月度的,则取 N =12 。若季节是季度的,则取N=4 。如果时间序列无 明显的周期变动,则可用自相关系数法来确定,即取 N 为高自相关系数的滞后时期。
k 的取值一般可定为1 / N,也可以用不同的k 值来进行计算,以确定一个能使S 小的k 值。

自适应滤波法有两个明显的优点:一是技术比较简单,可根据预测意图来选择权数 的个数和学习常数,以控制预测。也可以由计算机自动选定。二是它使用了全部历史数 据来寻求佳权系数,并随数据轨迹的变化而不断更新权数,从而不断改进预测。 由于自适应滤波法的预测模型简单,又可以在计算机上对数据进行处理,所以这种 预测方法应用较为广泛.























