经验风险函数的核心部分,也是结构风险函数重要组成部分。模型的结构风险函数包括了经验风险项和正则项,通常可以表示成如下式子:
Φ是正则化项(regularizer)或者叫惩罚项(penalty term),它可以是L1,也可以是L2,或者其他的正则函数。整个式子表示的意思是找到使目标函数最小时的θ值。下面主要列出几种常见的损失函数。
一、log对数损失函数(逻辑回归)
伯努利分布(0-1分布),然后求得满足该分布的似然函数,接着取对数求极值等等。而逻辑回归并没有求似然函数的极值,而是把极大化当做是一种思想,进而推导出它的经验风险函数为:最小化负的似然函数(即max F(y, f(x)) —-> min -F(y, f(x)))。从损失函数的视角来看,它就成了log损失函数了。
log损失函数的标准形式:
L(Y,P(Y|X))=−logP(Y|X)
刚刚说到,取对数是为了方便计算极大似然估计,因为在MLE中,直接求导比较困难,所以通常都是先取对数再求导找极值点。损失函数L(Y, P(Y|X))表达的是样本X在分类Y的情况下,使概率P(Y|X)达到最大值(换言之,
就是利用已知的样本分布,找到最有可能(即最大概率)导致这种分布的参数值;或者说什么样的参数才能使我们观测到目前这组数据的概率最大
)。因为log函数是单调递增的,所以logP(Y|X)也会达到最大值,因此在前面加上负号之后,最大化P(Y|X)就等价于最小化L了。
逻辑回归的P(Y=y|x)表达式如下:
P(Y=y|x)=11+exp(−yf(x))
将它带入到上式,通过推导可以得到logistic的损失函数表达式,如下:
L(y,P(Y=y|x))=log(1+exp(−yf(x)))
逻辑回归最后得到的目标式子如下:
之所以有人认为逻辑回归是平方损失,是因为在使用梯度下降来求最优解的时候,它的迭代式子与平方损失求导后的式子非常相似,从而给人一种直观上的错觉。
二、平方损失函数(最小二乘法, Ordinary Least Squares )
中心极限定理,最后通过极大似然估计(MLE)可以推导出最小二乘式子。最小二乘的基本原则是:最优拟合直线应该是使各点到回归直线的距离和最小的直线,即平方和最小。换言之,OLS是基于距离的,而这个距离就是我们用的最多的欧几里得距离。为什么它会选择使用欧式距离作为误差度量呢(即Mean squared error, MSE),主要有以下几个原因:
- 简单,计算方便;
- 欧氏距离是一种很好的相似性度量标准;
- 在不同的表示域变换后特征性质不变。
平方损失(Square loss)的标准形式如下:
L(Y,f(X))=(Y−f(X))2
当样本个数为n时,此时的损失函数变为:
Y-f(X)
表示的是残差,整个式子表示的是
残差的平方和
,而我们的目的就是最小化这个目标函数值(注:该式子未加入正则项),也就是最小化残差的平方和(residual sum of squares,RSS)。
而在实际应用中,通常会使用均方差(MSE)作为一项衡量指标,公式如下:
MSE=1n∑i=1n(Yi~−Yi)2
上面提到了线性回归,这里额外补充一句,我们通常说的线性有两种情况,一种是因变量y是自变量x的线性函数,一种是因变量y是参数
α
α
的线性函数。在机器学习中,通常指的都是后一种情况。
三、指数损失函数(Adaboost)
fm(x) fm(x):
α α
而指数损失函数(exp-loss)的标准形式如下
可以看出,Adaboost的目标式子就是指数损失,在给定n个样本的情况下,Adaboost的损失函数为:
关于Adaboost的推导,可以参考《统计学习方法》P145.
四、Hinge损失函数(SVM)
线性支持向量机中,最优化问题可以等价于下列式子: ![$$\min_{w,b} \ \sum_{i}^{N} [1 - y_i(w\cdot x_i + b)]_{+} + \lambda||w||^2 $$ leveneTest_机器学习_08](https://s2.51cto.com/images/blog/202410/15115626_670de7eac4dd988621.gif)
![$$[1 - y_i(w\cdot x_i + b)]_{+} = \xi_{i}$$ leveneTest_机器学习_09](https://s2.51cto.com/images/blog/202410/15115627_670de7eb3e75193413.gif)
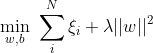

l l就是hinge损失函数,而后面相当于L2正则项。
Hinge 损失函数的标准形式
L(y)=max(0,1−yy~),y=±1
可以看出,当|y|>=1时,L(y)=0。
Hinge Loss函数能够保持支持向量机解的稀疏性。
正是因为HingeLoss的零区域对应的正是非支持向量的普通样本,从而所有的普通样本都不参与最终超平面的决定,这才是支持向量机最大的优势所在,对训练样本数目的依赖大大减少,而且提高了训练效率。
SVM用的Hinge Loss函数只有支持向量对分割面(线)有贡献,而LR的损失函数是所有样本点都对分割面(线)都有贡献。
-t参数分别是:
- 0-线性核;
- 1-多项式核;
- 2-RBF核;
- 3-sigmoid核。
五、其它损失函数
除了以上这几种损失函数,常用的还有:
0-1损失函数 

需要记住的是:参数越多,模型越复杂,而越复杂的模型越容易过拟合。过拟合就是说模型在训练数据上的效果远远好于在测试集上的性能。此时可以考虑正则化,通过设置正则项前面的hyper parameter,来权衡损失函数和正则项,减小参数规模,达到模型简化的目的,从而使模型具有更好的泛化能力。

![$$J(\theta) = - \frac{1}{m}\left [ \sum_{i=1}^m y^{(i)} \log h_{\theta}(x^{(i)}) + (1-y^{(i)}) \log(1-h_{\theta}(x^{(i)})) \right ]$$ leveneTest_leveneTest_02](https://s2.51cto.com/images/blog/202410/15115624_670de7e812f9855063.gif)
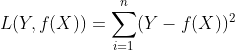

![$$\arg \min_{\alpha, G} = \sum_{i=1}^{N} exp[-y_{i} (f_{m-1}(x_i) + \alpha G(x_{i}))]$$ leveneTest_损失函数_05](https://s2.51cto.com/images/blog/202410/15115625_670de7e96104074842.gif)
![$$L(y, f(x)) = \exp[-yf(x)]$$ leveneTest_leveneTest_06](https://s2.51cto.com/images/blog/202410/15115625_670de7e9cd7a254568.gif)
![L(y, f(x)) = \frac{1}{n}\sum_{i=1}^{n}\exp[-y_if(x_i)] leveneTest_机器学习_07](https://s2.51cto.com/images/blog/202410/15115626_670de7ea528a391141.gif)






















