r语言 多重插补 r语言三次样条插值

自己以前上过数值分析这门课，用的是[1]这本教材，三次样条插值这一节，当时似乎看明白了，但在实际碰到它时，总觉得很神秘，也很心虚。过了好几年之后，想彻底理解这个cubic spline，就翻开以前的书看，看了老半天才看明白，上面写着很多乱七八糟的公式（当然也是有意义的），应该会像以前很快忘掉它们。之前看过Andrew NG写过的机器学习讲义，上面把各个公式娓娓道来，感觉很自然，也就理解的更深。于是乎，自己就在网上找老外是怎么讲这个的，[3]wiki百科也讲的迷迷糊糊的，后来搜到[2]，直接醍醐灌顶。

已知函数

在区间

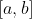
上的

个节点

  上的值

，求插值函数

，使得:

1.  ；
2. 在每个小区间上是三次多项式，记为；
3.  在 上二阶连续可微，

则函数

 称为

 的三次样条插值函数，

其中

是三次方函数，具有如下形式：

因此只要确定了这些系数

，就计算出了

，一共有

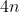
个系数需要确定。 首先根据

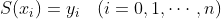
，可得：

  and 

则可得到

个方程：

    and   

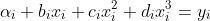
另外根据

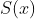
 在

 上二阶连续可微，我们需要在点

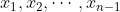
 上：

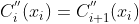
这两个方程可以写成：

这里有

个方程，加上之前的

个，目前总共有

个方程，而未知量有

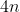
个，这时就需要边界条件来提供两个方程，常用的边界条件有以下三种：

1. 给定两端点处的导数值, 。特别地，当时，样条曲线在端点处呈水平状态。
2. 给定两端点处的二阶导数值,   。特别地，当时，称为自然边界条件。
3. 如果是以为周期的周期函数，则也应该是具有同样周期的周期函数，在端点处需要满足， 

值得注意的是，这

个方程是关于未知量的线性方程，因此很容易通过线性方程组进行求解。

这样以后想忘记都会很难，这里没有给出例子，如果有机会可以给出实现程序。