相关性分析主要用来描述变量之间的线性相关程度。
在二元变量的相关性分析过程中，常用的有Pearson相关系数，Spearman秩相关系数以及判定系数。
Pearson积矩相关系数
Pearson 相关评估两个连续变量之间的线性关系。当一个变量中的变化与另一个变量中的成比例变化相关时，这两个变量具有线性关系。
适用条件：
- 两个变量均应由测量得到的连续变量
- 两个变量所来自的总体都应该是正态分布，或接近正态的单峰对称分布。
- 变量必须是成对的数据。
- 两变量间为线性关系。
注意事项：
- 线性相关的前提条件是X、Y都是服从正态分布的。正态分布
- 当散点图有线性趋势时，才可以进行线性相关分析。
- 必须在假设检验认为相关的前提下才能以r的大小判断相关程度（显著性水平）。
- 相关关系并不一定是因果关系，有可能是伴随关系。
判断步骤：
- 找出两个变量的正确相应数据。
- 画出散点图，通过散点图判断相关性。
- 散点图有线性趋势时，计算相关系数
- 对结果进行评价和检验
相关系数的取值：
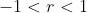
，大于0且越接近于1，则表示越是正相关；反转，小于0且越接近于-1则表示越是负相关。
等于0则认为零相关。
Spearman秩相关系数
是利用两变量的秩次大小作线性相关分析，对原始变量的分布不作要求，属于非参数统计方法，适用范围要广些。
对于服从Pearson相关系数的数据亦可计算Spearman相关系数，但统计效能要低一些。Pearson相关系数的计算公式可以完全套用Spearman相关系数计算公式，但公式中的x和y用相应的秩次代替即可
Spearman 相关评估两个连续或顺序变量之间的单调关系。在单调关系中，变量倾向于同时变化，但不一定以恒定的速率变化。Spearman 相关系数基于每个变量的秩值（而非原始数据）。
判定系数
判定系数是相关系数的平方。
计算积距Pearson相关系数，连续性变量才可采用;计算Spearman秩相关系数，适合于定序变量或不满足正态分布假设的等间隔数据。
研究表明，在正态分布的假设下，Pearson和Spearman在效率上是等价的，而对于连续测量数据，更适合Pearson相关系数来进行分析。在实际应用中，上述两种相关系数都需要对其进行假设检验，使用t检验方法检验其显著性水平以及确定其相关程度。
最好始终用散点图来检查变量之间的关系。相关系数仅度量线性 (Pearson) 或单调 (Spearman) 关系。也有可能存在其他关系。
本文章为转载内容，我们尊重原作者对文章享有的著作权。如有内容错误或侵权问题，欢迎原作者联系我们进行内容更正或删除文章。
