1.卷积层
这里,我们要实现一个拥有卷积层(CONV)和池化层(POOL)的网络,它包含了前向和反向传播。
1.1 边界扩充
首先实现两个辅助函数:一个用于零填充,另一个用于计算卷积。 边界填充将会在图像边界周围添加值为0的像素点,如下图

使用0填充边界有以下好处:
(1)卷积了上一层之后的CONV层,没有缩小高度和宽度。 这对于建立更深的网络非常重要,否则在更深层时,高度/宽度会缩小。 一个重要的例子是“same”卷积,其中高度/宽度在卷积完一层之后会被完全保留。
(2)它可以帮助我们在图像边界保留更多信息。在没有填充的情况下,卷积过程中图像边缘的极少数值会受到过滤器的影响从而导致信息丢失。
def zero_pad(X,pad):
X_paded = np.pad(X,(
(0,0), #样本数,不填充
(pad,pad), #图像高度,你可以视为上面填充x个,下面填充y个(x,y)
(pad,pad), #图像宽度,你可以视为左边填充x个,右边填充y个(x,y)
(0,0)), #通道数,不填充
'constant', constant_values=0) #连续一样的值填充
return X_paded1.2 卷积窗口
卷积窗口如下图所示:
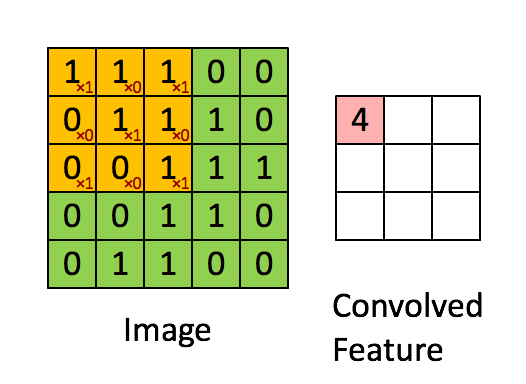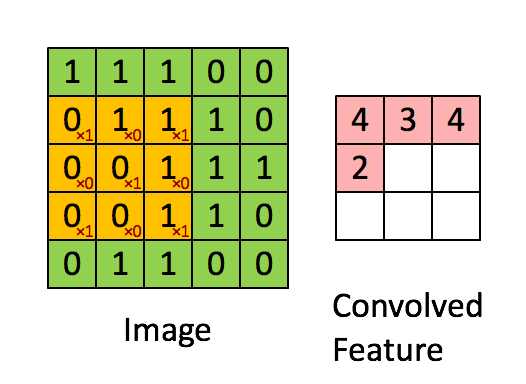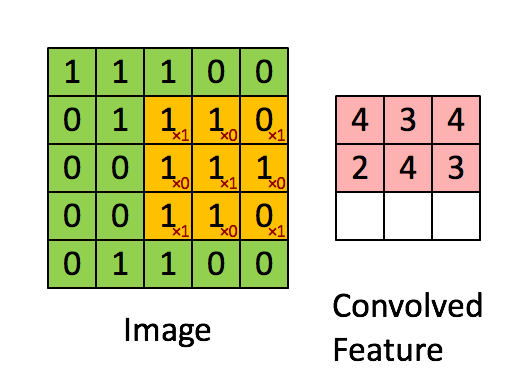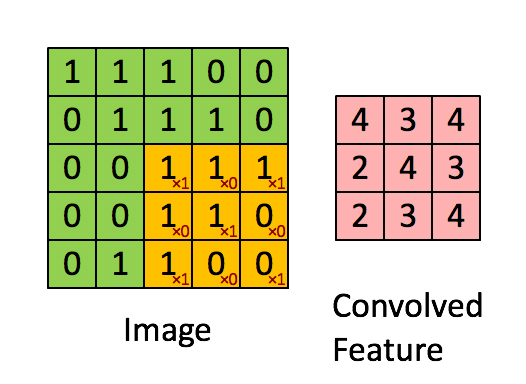
def conv_single_step(a_slice_prev, W, b):
s = np.multiply(a_slice_prev,W) + b
Z = np.sum(s)
return Z1.3 前向传播
在前向传播的过程中,我们将使用多种过滤器对输入的数据进行卷积操作,每个过滤器会产生一个2D的矩阵,我们可以把它们堆叠起来,于是这些2D的卷积矩阵就变成了高维的矩阵。
卷积公式
def conv_forward(A_prev, W, b, hparameters):
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
(f, f, n_C_prev, n_C) = W.shape
stride = hparameters["stride"]
pad = hparameters["pad"]
n_H = int(( n_H_prev - f + 2 * pad )/ stride) + 1
n_W = int(( n_W_prev - f + 2 * pad )/ stride) + 1
Z = np.zeros((m,n_H,n_W,n_C))
A_prev_pad = zero_pad(A_prev,pad)
for i in range(m):
a_prev_pad = A_prev_pad[i]
for h in range(n_H):
for w in range(n_W):
for c in range(n_C):
vert_start = h * stride #竖向,开始的位置
vert_end = vert_start + f #竖向,结束的位置
horiz_start = w * stride #横向,开始的位置
horiz_end = horiz_start + f #横向,结束的位置
a_slice_prev = a_prev_pad[vert_start:vert_end,horiz_start:horiz_end,:]
Z[i, h, w, c] = conv_single_step(a_slice_prev,W[: ,: ,: ,c],b[0,0,0,c])
assert(Z.shape == (m, n_H, n_W, n_C))
cache = (A_prev, W, b, hparameters)
return Z, cache1.4 反向传播
计算公式
函数实现
def conv_backward(dZ,cache):
(A_prev, W, b, hparameters) = cache
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
(m,n_H,n_W,n_C) = dZ.shape
(f, f, n_C_prev, n_C) = W.shape
pad = hparameters["pad"]
stride = hparameters["stride"]
dA_prev = np.zeros((m,n_H_prev,n_W_prev,n_C_prev))
dW = np.zeros((f,f,n_C_prev,n_C))
db = np.zeros((1,1,1,n_C))
A_prev_pad = zero_pad(A_prev,pad)
dA_prev_pad = zero_pad(dA_prev,pad)
for i in range(m):
a_prev_pad = A_prev_pad[i]
da_prev_pad = dA_prev_pad[i]
for h in range(n_H):
for w in range(n_W):
for c in range(n_C):
vert_start = h
vert_end = vert_start + f
horiz_start = w
horiz_end = horiz_start + f
a_slice = a_prev_pad[vert_start:vert_end,horiz_start:horiz_end,:]
da_prev_pad[vert_start:vert_end, horiz_start:horiz_end,:] += W[:,:,:,c] * dZ[i, h, w, c]
dW[:,:,:,c] += a_slice * dZ[i,h,w,c]
db[:,:,:,c] += dZ[i,h,w,c]
dA_prev[i,:,:,:] = da_prev_pad[pad:-pad, pad:-pad, :]
assert(dA_prev.shape == (m, n_H_prev, n_W_prev, n_C_prev))
return (dA_prev,dW,db)2.池化层
池化层会减少输入的宽度和高度,这样它会较少计算量的同时也使特征检测器对其在输入中的位置更加稳定。下面介绍两种类型的池化层:
最大值池化层:在输入矩阵中滑动一个大小为fxf的窗口,选取窗口里的值中的最大值,然后作为输出的一部分。
均值池化层:在输入矩阵中滑动一个大小为fxf的窗口,计算窗口里的值中的平均值,然后这个均值作为输出的一部分。


2.1 前向传播
池化层计算公式与卷积层一致:
def pool_forward(A_prev, hparameters, mode = "max"):
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
f = hparameters["f"]
stride = hparameters["stride"]
n_H = int(1 + (n_H_prev - f) / stride)
n_W = int(1 + (n_W_prev - f) / stride)
n_C = n_C_prev
A = np.zeros((m, n_H, n_W, n_C))
for i in range(m):
for h in range(n_H):
for w in range(n_W):
for c in range (n_C):
vert_start = h * stride #竖向,开始的位置
vert_end = vert_start + f #竖向,结束的位置
horiz_start = w * stride #横向,开始的位置
horiz_end = horiz_start + f #横向,结束的位置
a_prev_slice = A_prev[i,vert_start:vert_end,horiz_start:horiz_end,c]
if mode == "max":
A[i, h, w, c] = np.max(a_slice_prev)
elif mode == "average":
A[i, h, w, c] = np.mean(a_slice_prev)
cache = (A_prev, hparameters)
assert(A.shape == (m, n_H, n_W, n_C))
return A, cache2.2 创建掩码
在开始池化层的反向传播之前,我们需要创建一个函数,这个函数创建了一个掩码矩阵,以保存最大值的位置,当为1的时候表示最大值的位置,其他的为0,这个是最大值池化层,均值池化层的向后传播也和这个差不多,但是使用的是不同的掩码。
最大值池化层的反向传播
def create_mask_from_window(x):
mask = x == np.max(x)
return mask均值池化层的反向传播
在最大值池化层中,对于每个输入窗口,输出的所有值都来自输入中的最大值,但是在均值池化层中,因为是计算均值,所以输入窗口的每个元素对输出有一样的影响。
2.3 反向传播
接下来,我们从最大值池化层开始实现池化层的反向传播。 即使池化层没有反向传播过程中要更新的参数,我们仍然需要通过池化层反向传播梯度,以便为在池化层之前的层(比如卷积层)计算梯度。
def pool_backward(dA,cache,mode = "max"):
(A_prev , hparaeters) = cache
f = hparaeters["f"]
stride = hparaeters["stride"]
(m , n_H_prev , n_W_prev , n_C_prev) = A_prev.shape
(m , n_H , n_W , n_C) = dA.shape
dA_prev = np.zeros_like(A_prev)
for i in range(m):
a_prev = A_prev[i]
for h in range(n_H):
for w in range(n_W):
for c in range(n_C):
vert_start = h
vert_end = vert_start + f
horiz_start = w
horiz_end = horiz_start + f
if mode == "max":
a_prev_slice = a_prev[vert_start:vert_end,horiz_start:horiz_end,c]
mask = create_mask_from_window(a_prev_slice)
dA_prev[i,vert_start:vert_end,horiz_start:horiz_end,c] += np.multiply(mask,dA[i,h,w,c])
elif mode == "average":
da = dA[i,h,w,c]
shape = (f,f)
dA_prev[i,vert_start:vert_end, horiz_start:horiz_end ,c] += distribute_value(da,shape)
assert(dA_prev.shape == A_prev.shape)
return dA_prev卷积神经网络参数计算
Activation shape | Activation size | h parameters | parameters | |
Input | (32,32,3) | 32* 32 *3=3072 | f=5,s=1 | 0 |
conv1 | (28,28,8) | 28* 28 *8=6272 | p=2,s=2 | (5 * 5+1)*8 |
pool1 | (14,14,8) | 14* 14 *8=1568 | f=5,s=1 | 0 |
conv2 | (10,10,16) | 10* 10 *16=1600 | p=2,s=2 | (5 * 5+1)*16 |
pool2 | (5,5,16) | 5* 5 *16=400 | 0 | |
fc3 | (120,1) | 120 | 400*120+1 | |
fc4 | (84,1) | 84 | 120*84+1 | |
softmax | (10,1) | 10 | 84*10+1 |
参考吴恩达DeepLearning.ai






















