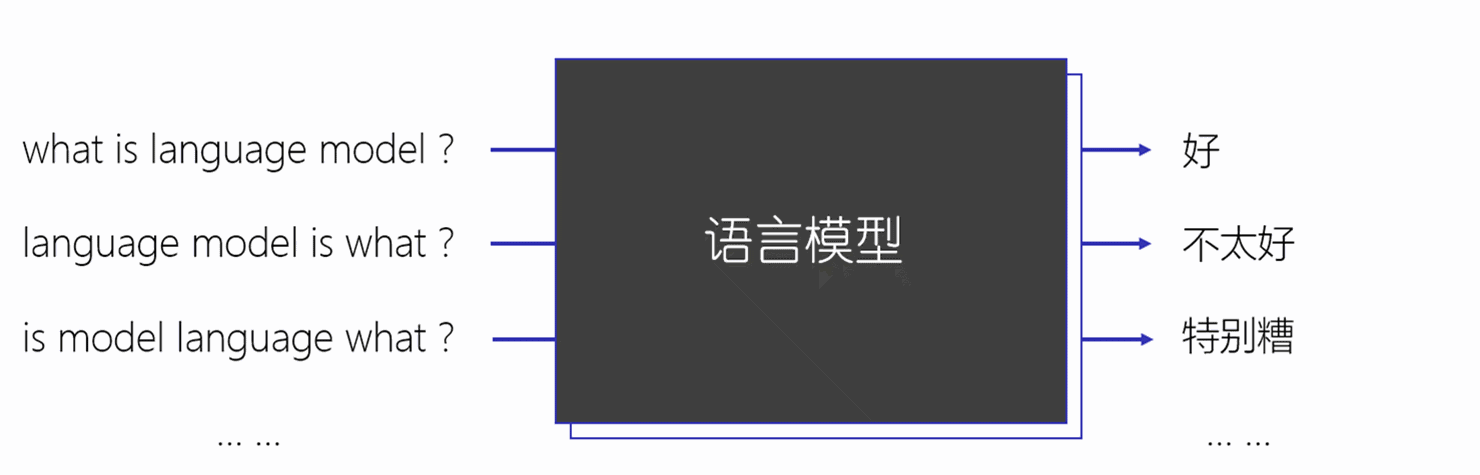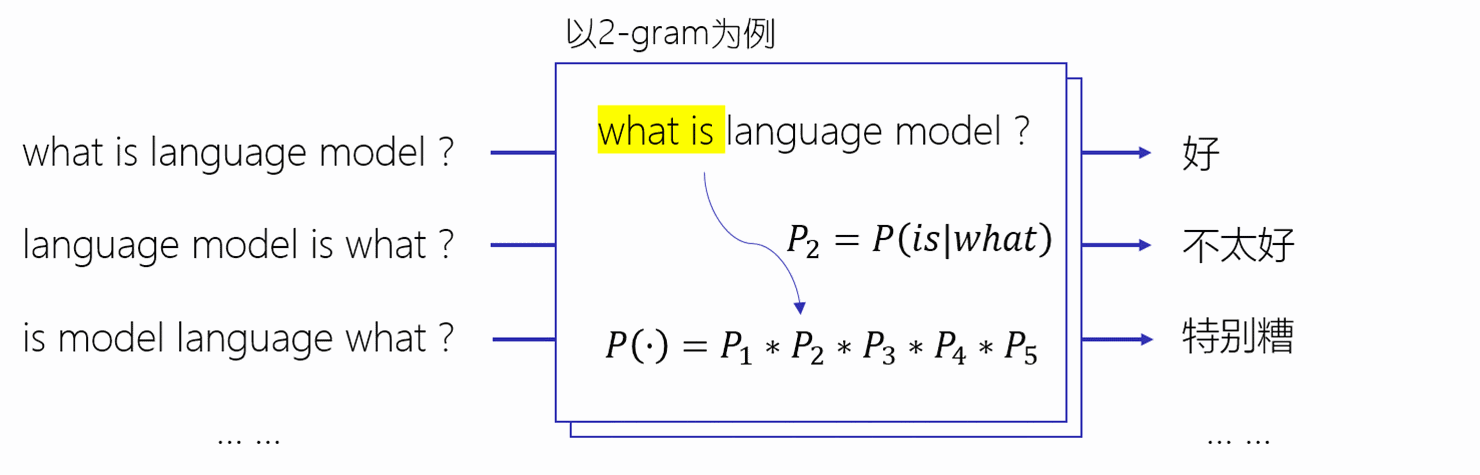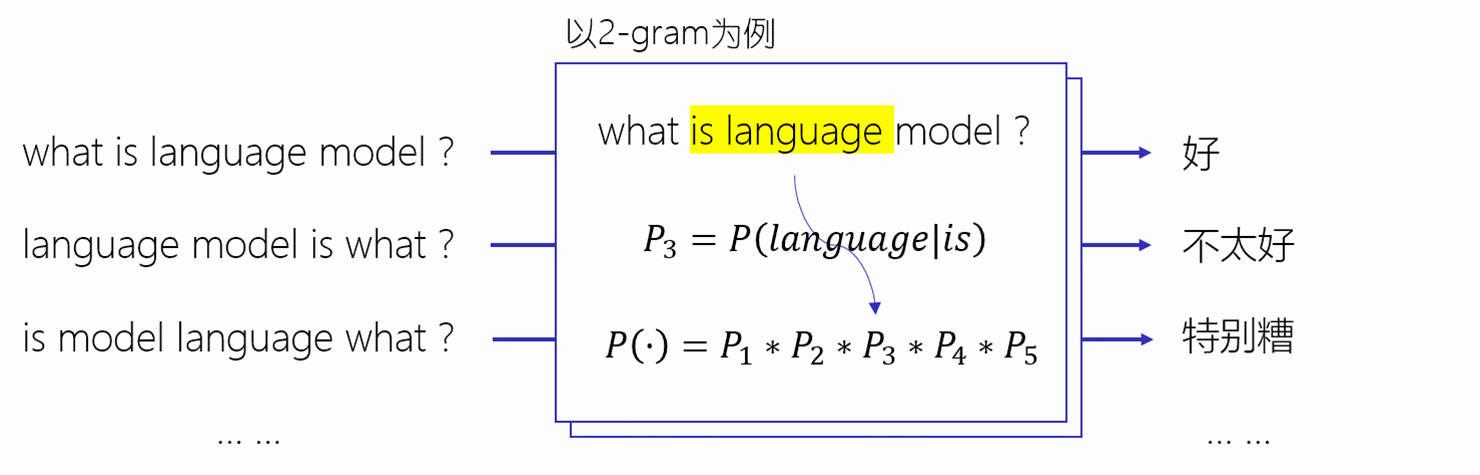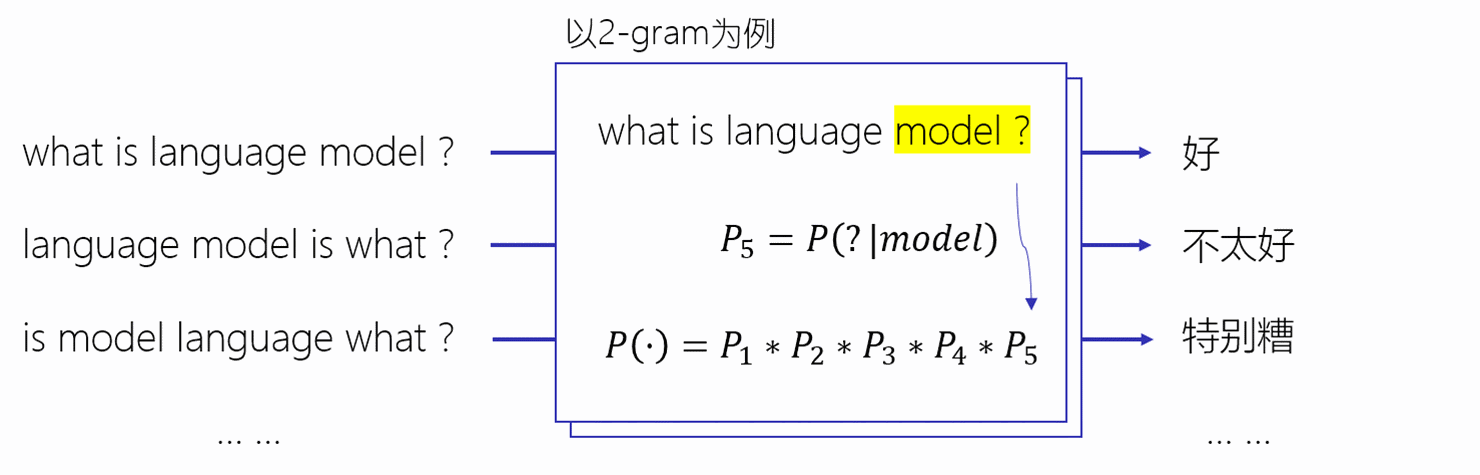
  上一篇[文章](第15天:NLP--语言模型(上)_Oliverfly1的博客-CSDN博客)我们介绍了语言模型的相关理论,包括Nosiy Channel Model、Chain Rule以及很典型的Markov Assumption,另外就是介绍了Unigram、 Bigram 以及N-gram模型,然后就是估计语言模型的概率,还有就是评估语言模型,其中就是Perplexity,前面也提到过,之前计算N-gram模型计算语言模型概率的时候,存在已很很重要的问题那就是对于稀疏性问题,也就是对于语言模型中其中一项概率为0,则其他整个句子的概率模型就是为0,接下来,我们给大家介绍一种方式来解决这种情况。整体思路就是用平滑,通过增加一个小的项,使其没有出现在语料库中的概率不为0.
## Smoothing(平滑处理)
  平滑的方式有很多种,其中主要包括Add-one Smoothing也就是我们常说的Laplace Smoothing,还有就是Add-K Smoothing,当K=1时,其就是拉普拉斯平滑。接着就是Interpolation和最后的Good—Turning Smoothing。首先给大家介绍Laplace Smoothing。
### Add-one Smoothing 方法(Laplace Smoothing 方法)
  为了解决零概率的问题,法国数学家拉普拉斯最早提出用加1的方法估计没有出现过的现象的概率,所以加法平滑也叫做拉普拉斯平滑。假定训练样本很大时,每个分量x的计数加1造成的估计概率变化可以忽略不计,但可以方便有效的避免零概率问题。若不考虑Smoothing,通常计算的是P~MLE~ 如图所示:

  但是此方法可能出现P(Wn)为0的情况而导致无法评估,因此引入Smoothing方法。具体实现如下:

这里需要说明的是:
- V是词典的大小(无重复词)
- 在分母中加V,会使得所有P()的总和为1
举一个简单的例子来说明该问题:
假设我们的V=20;C(我们)=3,C(我们,是)=0,这里我们分别计算他们的概率如下:
举一个简单的例子来说明该问题:
假设我们的V=20;C(我们)=3,C(我们,是)=0,这里我们分别计算他们的概率如下:

假设有以下的语料库,通过用拉普拉斯计算可的结果如下:


Add-One Smoothing完美的规避了出现0的问题,但是,由于训练的语料中未出现的n-gram数量太多,平滑后,所有未出现的n-gram占据了整个概率分布中的一个很大的比例。因此,Add-One Smoothing给定训练的语料中没有出现过的n-gram分配了太多的概率空间。因此,接下来我们给大家介绍另一种Smoothing——Add-K Smoothing。
Add-K Smoothing(Laplace Smoothing)
其实Add-K Smoothing是由Add-one衍生出来的另外一种算法Add-K,既然我们认为加1有点过了,不然选择一个小于1的正数 k。此时,概率计算公式就变成了

还是上面的语料库,我们用Add-K Smoothing来计算其语言模型的概率,当k=3时,计算结果如下:

这路需要我们注意的是,当K=1时,Add-K Smoothing就是Add-one Smoothing。通常,add-k算法的效果会比Add-one好,但是显然它不能完全解决问题。至少在实践中,k 必须人为给定,而这个值到底该取多少,怎么取却是一个很大的问题。
初步是K = 1,2,3…n ,一个一个计算对比找到最合适的 k;还有就是优化 f(k) ,此时Perplexity = f(k),故 Minperplexity= Minf(k) => k= argmink f(k)。
Interpolation 方法
通过上述对两种Smoothing方法的介绍,但是现在不出现的概率,不代表未来数据更多anyway还不出现。这里实现的核心就是在计算Trigram概率时同时Unigram, Bigram以及n-gram出现的频次。具体如下:


Good-Turning Smoothing
在介绍Good-Turning Smoothing之前,我们可以先看一个有趣的例子:
假设你在钓鱼,已经抓到了18只鱼:【10条鲤鱼,3条黑鱼,2条刀鱼,1条鲨鱼,1条草鱼,1条鳗鱼…】
Q1:下一个钓到的鱼是鲨鱼的概率是多少?
Q2:下一条鱼是新鱼种(之前没有出现过)的概率是多少?
Q3:既然如此,重新想一下,下一条抓到鱼为鲨鱼的概率是多少?
我们在看到Q1时,可以很简单的算出Q1结果为 1/18.
但是到了Q2,此时概率是无法计算的,所以我们便可以在此引出Good-Turning。在Good-Turning方法论中,我们会假设未出现过的鱼种的概率与出现一次的鱼种的概率相同,即N_0 = N_1 (N_k表示出现k次的元素的总数),在上面的例子中N_10=1,N_3=1,N_2=1,N_1=3。然后我们回到Q2,此时Q2的结果也为3/18,即1/6。
然后我们继续看Q3,因为没有出现的鱼种出现的概率有1/6,所以Q1的结果应该小于1/18。
在Good-Turning方法论中,当我们要求一个元素c出现的概率时,会先计算:

这里需要申明的是:N^c^: 出现c次的单词的个数。然后再通过原本的概率算出新的概率,即P(鲨鱼)=(1+1) * 1/3 * (1/18) = 1/27。

其实,Good-Turing算法的思想是,对于出现次数大于某一阈值的ngram使最大似然用频率计算是比较准确的,但是如果小于这个阈值,最大似然估计就不准了。这时候,算法的处理就是利用出现次数较多的N阶元组去调整出现比他少的N阶元组的估计量。接下来可以拿实际使用的场景距离,再次进行推导:
假如我们有一个长度我c的词库,每次从中抽出1个次,由训练集放入验证集中,循环c次获得了c个训练数据。每次去掉一个单词,最后获得c个训练数据(每一个包含c-1个单词)。
Q1:在验证集中,百分之多少的单词没有出现在训练集中?
Q2:验证集中百分之多少的单词在训练集中出现K次?
在Q1中,因为只有出现1次的单词,从训练数据集中拿出后,就不会再出现了,所以Q1的结果为 N1/C。同理,我们需要单词在训练集中出现K次,则拿过来的单词原本应该出现K+1次,所以Q2的结果应该是N(K+1)(K+1)/C。再继续,假如此时我们只需要求得其中1个单词出现K次的概率,则再Q2中,分母上乘以一个Nk就可以了,即N(K+1)(K+1)/(CNk)。

我们在拉普拉斯平滑中,知道平滑向是:但是此时的1,是一个频次,然后我们上面算出来的是一个概率,要将概率转换为频次,即乘以一个C(词库大小)就可以了,即N(K+1)(K+1)/*Nk,与前面得到的结果一致:

下面是一个实际的词频统计的例子:第一列是单词出现次数,第二列是出现r次的单词的数量,第三列是我们的期望概率:

其中,第三列的期望概率就是通过上述结论计算出来的,例如:
P(1) = (1+1)*263611/1132844 = 0.46539
P(2) = (2+1)*123615/263611 =1.40679
最后讲一下这个方法论的缺点:
从上图中也可以看出,当单词出现次数慢慢增大时,r值并不是连续性的,但是每一个P(r )的计算都依赖于r+1的count值。也就是:计算Ni-1,需要Ni,很多情况会有Nn的缺失
简单的解决方案是,我们可以通过线性回归之类的方法,平滑的推断出7、9等不存在的r值的对应的count值,然后再带入上式进行计算。即:根据现有Nn的情况作一条曲线(机器学习的方法拟合)来估计缺失值。
Use Language Model to Generate Sentence
当一个模型训练好后,我们可以利用这个模型来生成一些数据,就是生成模型。例如:生成句子,音乐,图像,程序等。假如给定我们一个词库,然后每一个词对应的概率已经训练好了,然后用Unigram来生成一个句子。由于Unigram是不考虑上下文的,所以这个句子完全就随机根据单词的概率取的下一个词。当然,我们也可以用Bigram生成一个句子。先根据词库写出每个词后面接另外一个词的概率矩阵,大小是7*7,包含了6个单词和一个终止符,如果第一个单词采样到I,那么可以从矩阵上可以看到,I后面跟like的几率最大。这样以此类推,直到采样到句号为止。如果Bigram的模型训练得很好,通过采样得到的语句是比较通顺的,因此优于unigram。如果有大量的语料基础上,可以训练N-gram。
总结
通过上一篇文章对语言模型的介绍,了解了语言模型的计算过程以及评估一个语言模型的具体方法。但是我们在文章的最后也提到,那些方法也存在一些弊端,比如说稀疏性问题,只要其中有一项概率为0,则整个句子的概率就为0,这是一个很严重的情况。接下来,为了解决这一问题,我们采用了平滑的方式解决该问题,包括Add-one Smoothing 也是我们经常提到的Laplace Smoothing 方法,但是这种方法也存在一定的问题,后面又介绍了一种Add-K Smoothing的方法,其实就是对Laplace Smoothing 方法的延伸。对于K的选择以及没有考虑到未来出现情况的概率。因此有介绍了一种Interpolation 方法以及Good-Turning Smoothing。最后在学习了这些处理语言模型存在稀疏性问题的各种平滑的方法之后,我们又大致给大家介绍了利用语言模型生成句子,可以通过ungram model、Bigram model以及N-gram,通过这些模型,我们可以生成很多语义通顺的句子。总之,语言模型在NLP中还是很重要的一块,需要我们重点掌握,因此,我们得好好的下点功夫把这一块知识吃透。加油吧,各位。NLP工程师未来可期,在追梦的道路上不断前行。最后送大家一句“Life is like a box of chocolates that you will never know what you gonna get. Never give up!!!”





















