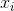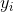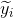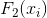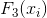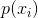Gradient Boost的算法流程

备注:这里
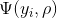
表示损失函数,
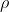
表示样本在相对于决策面(后续分析回归问题和分类问题)的得分。
About Logistic
对于二分类任务而言,常常采用Log-loss:
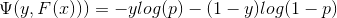
,其中
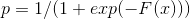
与算法流程相对应,为了便于后续推导方便,这里对Log-loss进行化简:

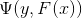
关于得分F(x)的一阶、二阶导数为:
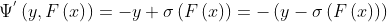
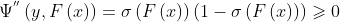
如果采用Log-loss后使用GBDT关于二分类任务的算法,则有:

在第m轮的学习中,CART的第j个叶子节点
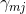
的得分的推导公式:

Log_TreeBoost
About Softmax
对于多分类任务而言,常常采用softmax:

对应的一阶导数:

求解叶子节点的目标函数:

解得叶子得分:

Sm_TreeBoost

算例
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
表1.数据集信息
参数的设置:
- loss函数:Log-loss;
- 回归树的分裂准则:MSE;
- 树的深度:1(即决策树桩)
- 学习率:0.1;
step - 1 : 初始化算法
首先,计算
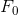
的取值:
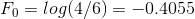
利用GBDT-Logloss算法中step-2a计算loss函数关于
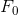
的负梯度 :

带入上述结果,得到各样本在loss函数中关于
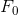
的负梯度:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| -0.4 | -0.4 | -0.4 | 0.6 | 0.6 | -0.4 | -0.4 | -0.4 | 0.6 | 0.6 |
表2.loss函数关于
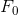
的负梯度
step - 2 : 拟合第一棵树
若采用MSE作为分裂准则,首先规范几个符号:
MSE(x=val) = { var(L) * |L| + var(R) * |R| } / (|L| + R|)
其中,L={x|x<=val},R={x|x>val},|L|、|R|依次表示集合L和R中元素的个数,var表示计算集合元素的方差。【这里特别感谢csuyhb的提醒】
若以x1为分裂点,则MSE(x=x1) = {var({-0.4})*1 + var({-0.4, -0.4, 0.6, 0.6, -0.4, -0.4, -0.4, 0.6, 0.6}) *9}/10 = 0.2222;
若以x2为分裂点,则MSE(x=x2) = {var({-0.4, -0.4})*2 + var({-0.4, 0.6, 0.6, -0.4, -0.4, -0.4, 0.6, 0.6})*8}/10 = 0.2000;
其它分裂点类似,可得如下结果:
分裂点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
mse | 0.2222 | 0.2000 | 0.1714 | 0.2250 | 0.2400 | 0.2333 | 0.2095 | 0.1500 | 0.2000 | 0.2400 |
表3.基于表2得到的各分裂点对应的MSE
易知,最优划分点为split_point = x8,从而得到如下的决策树桩:

计算左、右两侧叶子的预测值,由公式:

可得
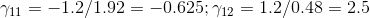
。更新
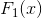
:

这里
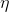
表示学习率,学习率过小,导致算法收敛过慢;反之,则容易导致算法在迭代过程中产生震荡,容易陷入局部最优。这 里我们取

,得到表4所示的
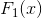
对数据集的预测得分为:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| -0.468 | -0.468 | -0.468 | -0.468 | -0.468 | -0.468 | -0.468 | -0.468 | -0.1555 | -0.1555 |
表4. F1(x)对各样本的预测得分
同样,利用下式可以得到Log-loss关于
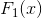
的负梯度:

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| -0.3851 | -0.3851 | -0.3851 | 0.6149 | 0.6149 | -0.3851 | -0.3851 | -0.3851 | 0.5388 | 0.5388 |
表5. Log-loss函数关于
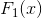
的负梯度
step - 3 : 拟合第2棵树
与计算第二棵树时过程类似,首先基于表5计算各分裂点的mse:
分裂点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
mse | 0.2062 | 0.1856 | 0.1592 | 0.2106 | 0.2224 | 0.2187 | 0.1998 | 0.1500 | 0.1904 | 0.2227 |
表6. 基于表5得到的各分裂点对应的MSE
对应的最优划分点为split_point = 8,得到与第一个树相同的决策树桩。进一步得到左、右两侧叶子的预测值为:
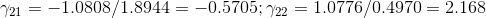
. 得到
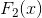
对数据集的预测得分为:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| -0.5251 | -0.5251 | -0.5251 | -0.5251 | -0.5251 | -0.5251 | -0.5251 | -0.5251 | 0.0613 | 0.0613 |
表7. F2(x)对各样本的预测得分
类似地,我们得到
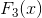
对数据集的预测得分为:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| -1.0461 | -1.0461 | -1.0461 | -1.0461 | -1.0461 | -1.0461 | -1.0461 | -1.0461 | 2.0018 | 2.0018 |
表8. F3(x)对各样本的预测得分
通过sigmod函数将上述得分转换为概率:

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0.2600 | 0.2600 | 0.2600 | 0.2600 | 0.2600 | 0.2600 | 0.2600 | 0.2600 | 0.8810 | 0.8810 |
表9. F3(x)对各样本的预测概率
Inference
[1] . Jerome Friedman. Greedy function approximation: a gradient boosting machine[2001]
[2].