一、交换类(transposition)排序
1、冒泡(Bubble)排序:
时间复杂度:O(n^2); 空间复杂度:O(1)
原理:进行n-1次循环,每次循环可以排好一个最大值。相邻的两个数进行比较,是最大值不断后移(类似于气泡上浮)
代码实现:
public static void get_sort(int[] arr) {
//冒泡排序
for(int i=0;i<arr.length-1;i++) { //需要浮动n-1次(当n-1个值排好序后,剩下的一定为最小值)
for(int j=0;j<arr.length-i-1;j++) {//对相邻的元素进行比较,筛选出最大值,上浮
if(arr[j]>arr[j+1]) {
int temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}是所有排序算法中最慢的算法
2、快速排序
时间复杂度:O(n*logN)空间复杂度:O(1)
原理: 它利用分治法来对待排序序列进行分治排序,其主要是通过一趟排序将待排记录分隔成独立的两部分,其中的一部分比关键字小,后面一部分比关键字大,然后再对这前后的两部分分别采用这种方式进行排序,通过递归的运算最终达到整个序列有序。
代码实现:
public static void Quick(int[] arr,int begin,int end) {
if(begin<end) {
int i,j,temp,temp2;
temp=arr[begin];
i=begin; //必须是begin,避免进行强制交换
j=end;
while(i<j) {
while(i<j && arr[j]>=temp) { //必须先右面递减,必须得带等号,因为与temp交换的目的是 将temp调整到合适的额位置
j--;
}
while(i<j && arr[i]<=temp) {
i++;
}
if(i<j) {
temp2=arr[i];
arr[i]=arr[j];
arr[j]=temp2;
}
}
arr[begin]=arr[j]; //将关键字放于正确的位置上
arr[j]=temp;
Quick(arr,begin,j-1);
Quick(arr,j+1,end);
}
}参考链接:
二、插入类排序
3、插入排序
时间复杂度:O(n^2) 空间复杂度:O(1)
原理:它的工作原理是通过构建有序序列(数组),对于未排序数据(基准元素),在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
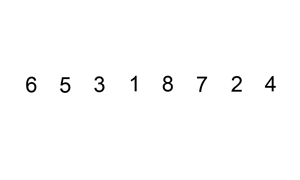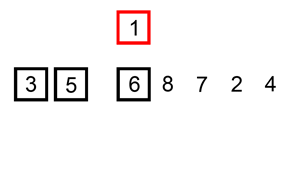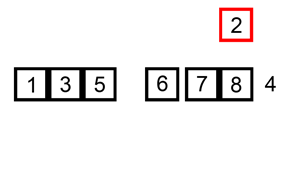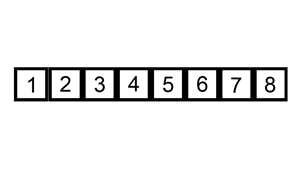
代码实现:
public static void insert(int [] arr) {
for(int i=1;i<arr.length;i++) {
int temp=arr[i]; //保存基准元素
int j=i-1; //定义比较元素
while(j>=0 && arr[j]>temp) { //将所有元素分别于基准元素比较
arr[j+1]=arr[j]; //元素后移
j--;
}
arr[j+1]=temp; //将基准元素插入到合适的位置(因为第j个元素一定不大于temp)
}
}4、希尔排序(Shell Sort)
空间复杂度:O(1) ; 时间复杂度:不确定,在平均状况下为O(n^1.3)
原理:是插入排序的一种是对插入排序的优化。将数组列在一个表中,并对列分别进行插入排序,重复这过程,不过每次用更长的列(步长更长了,列数更少了)来进行。最后整个表就只有一列了。
实现:
public static void insert(int [] arr) {
for(int gap=arr.length/2;gap>0;gap/=2) { //进行间隔的分类
for(int i=gap*1;i<arr.length;i++) { //选取第二个元素
int temp=arr[i];
int j=i-gap;
while( j>=0 && arr[j]>temp ) { //进行判断
arr[j+gap]=arr[j];
j-=gap;
}
arr[j+gap]=temp;
}
}
}参考链接:
三、选择类排序
5、选择排序(Selection Sort)
时间复杂度:O(n^2); 空间复杂度:O(1)
原理:进行n-1次循环,每次循环中可以排列出最小值放于最前面:选择X[i]与其以后的元素的最小值进行交换,来确保X[i]是最小值
代码实现:
public static void selection(int[] arr) {
for(int i=0;i<arr.length;i++) {
int swap=i; //依次对n个元素进行排序,共需要n-1次循环
for(int j=i+1;j<arr.length;j++) {
if(arr[swap]>arr[j]){
swap=j; //始终保证swap是最小值对应的索引
}
}
if(swap!=i) { //若不是原索引,则进行交换,确定最小的元素
int temp=arr[swap];
arr[swap]=arr[i];
arr[i]=temp;
}
}
for(int i:arr) {
System.out.print(i+" ");
}
System.out.println();
}6、堆排序(Heap Sort)
时间复杂度:O(nlogN); 空间复杂度:O(n)
堆是具有以下性质的 完全二叉树 :每个结点的值都大于或等于其 左右 孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其 左右 孩子结点的值,称为小顶堆。
堆排序:堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
原理:将待排序序列构造成一个 大顶堆 ,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个大顶堆,这样会得到n-1个元素的次小值。如此反复执行,便能得到一个有序序列了。大顶堆时升序排列;小顶堆时降序排列

代码实现:
public static void heap_sort(int[] arr) {
for(int i=(arr.length-1)/2;i>=0;i--) {//首先将数据调整为一个堆
adjust(arr,i,arr.length-1);
}
for(int i=arr.length-1;i>0;i--) {//,调换数据的顺序,并且将生育元素调整为一个堆
int temp=arr[i];
arr[i]=arr[0];
arr[0]=temp;
adjust(arr,0,i-1);
}
}
public static void adjust(int[] arr,int start,int end) {
int temp=arr[start];
for(int i=start*2+1;i<=end;i=i*2+1) {
if(i+1<=end &&arr[i+1]>arr[i]) { //取子节点的最大值,此处必须为&&以保证索引不会越界
i++;
}
if(arr[i]>temp) { //将子节点的值,给父节点
arr[start]=arr[i];
start=i;
}else {
break;
}
}
arr[start]=temp;//将temp放到合适的位置
}参考链接:
7、归并排序
时间复杂度:O(nlogN) 空间复杂度:O(n)
***原理:***:归并排序和快速排序一样,利用的是分治的思想实现的。归并排序对于给定的一组数据,利用递归与分治技术将数据序列划分成为越来越小的子序列,之后对子序列排序,最后再用递归方法将排好序的子序列合并成为有序序列。合并两个子序列时,需要申请两个子序列加起来长度的内存,临时存储新的生成序列,再将新生成的序列赋值到原数组相应的位置。
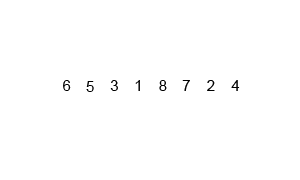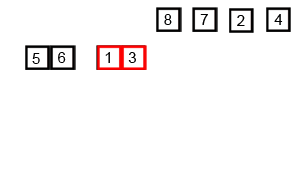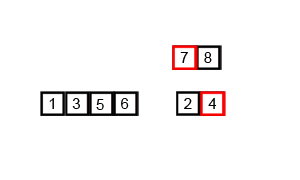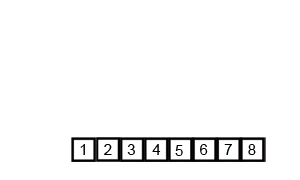
代码实现:
public static void merge_sort(int[] arr,int start,int end) { //此函数中的所有arr都是原arr,因为改变的是地址
if(start<end) { //当只有一个元素的时候退出
int mid=(start+end)/2;
merge_sort(arr,start,mid);
merge_sort(arr,mid+1,end);
merge(arr,start,mid,end);//将数据按照顺序合并
}
}
public static void merge(int[] arr,int start,int mid,int end) {
int[] a=new int[end-start+1]; //辅助数组
int p1=start;
int p2=mid+1;
int k=0;
while(p1<=mid && p2<=end) {
if(arr[p1]<arr[p2]) {
a[k++]=arr[p1++];
}else {
a[k++]=arr[p2++];
}
}
while(p1<=mid) { //如果第一个序列未检测完,直接将后面所有元素加到合并的序列中
a[k++]=arr[p1++];
}
while(p2<=end) {
a[k++]=arr[p2++];
}
for( int i=0;i<a.length;i++) {//将已经比较好的值赋值给数组
arr[i+start]=a[i];
}
}参考链接:
五、线性时间非比较类排序
8、计数排序(Count Sort)
时间复杂度 O(n+k) 空间复杂度:O(k)
K为数组的最大值,因为空间复杂度与时间复杂度都与K有关,所以数组的最大值不能过大,且数组中元素都为自然数,所有元素不能有负数
原理:对于给定的输入序列中的每一个元素x,确定该序列中值小于x的元素的个数。一旦有了这个信息,就可以将x直接存放到最终的输出序列的正确位置上。例如,如果输入序列中只有17个元素的值小于x的值,则x可以直接存放在输出序列的第18个位置上。当然,如果有多个元素具有相同的值时,我们不能将这些元素放在输出序列的同一个位置上,在代码中作适当的修改即可。
代码实现:
public static void countingSort( int[] arr,int k) {//k为数组arr的最大值,所以最大值必须已知
int[] arr1=new int [k+1];
int [] arr2=new int[arr.length];
for(int i=0;i<arr.length;i++) { //统计每个值出现的次数
arr1[arr[i]]++;
}
int sum=0;
for(int i=0;i<arr1.length;i++) {//统计每个值的大小(从一开始)
sum+=arr1[i];
arr1[i]=sum;
}
print(arr1);
for(int i=0;i<arr.length;i++) { //对数组赋值,不明白为什么要倒序赋值??????????个人觉得正序也可以
arr2[arr1[arr[i]]-1]=arr[i];
arr1[arr[i]] -= 1; //一定要加,防止重复元素消失,这样可使重复的元素依次向前输出
}
print(arr2);
}参考链接:
为啥一定要逆序赋值???????????(没理解这样做的原因,欢迎解答!!!!)
9、基数排序(Radix Sort)
时间复杂度:O(N^k(最大数的位数)); 空间复杂度:O(n)
原理: :基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯(即通过个位,十位,百位…),将要排序的元素分配至某些“桶”中,藉以达到排序的作用,基数排序法是属于稳定性的排序,其时间复杂度为O (nlog®m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的稳定性排序法。个人感觉很像计数排序,但是增加了循环次数,减少了空间复杂度
代码实现
public static int get_max(int[] arr) {
int m=arr[0];
for(int i=1;i<arr.length;i++) {
if(m<arr[i]) {
m=arr[i];
}
}
return (m+"").length();
}
public static int get_num(int number,int num) {
int[] a = {1,10,100};
return (number/a[num-1])%10;
}
public static void countingSort( int[] arr,int k) {//k为数组arr的最大值的位数
int [] bucket=new int[arr.length];
int[] count=new int [10];
for( int w=1;w<=k;w++) {
for(int i=0;i<count.length;i++) {
count[i]=0;
}
for(int i=0;i<arr.length;i++) { //统计每个值出现的次数
count[get_num(arr[i],w)]++;
}
int sum=0;
for(int i=0;i<count.length;i++) {//统计每个值的大小(从一开始)
sum+=count[i];
count[i]=sum;
}
for(int i=arr.length-1;i>=0;i--) { //对数组赋值,不明白为什么要倒序赋值?个人觉得正序也可以
int x=get_num(arr[i],w);
bucket[count[x]-1]=arr[i];
count[x] -= 1; //一定要加,防止重复元素消失,这样可使重复的元素依次向前输出
}
for( int i=0;i<arr.length;i++) { //将数组元素给arr,重新排序
arr[i]=bucket[i];
}
}
print(arr);
}参考链接:
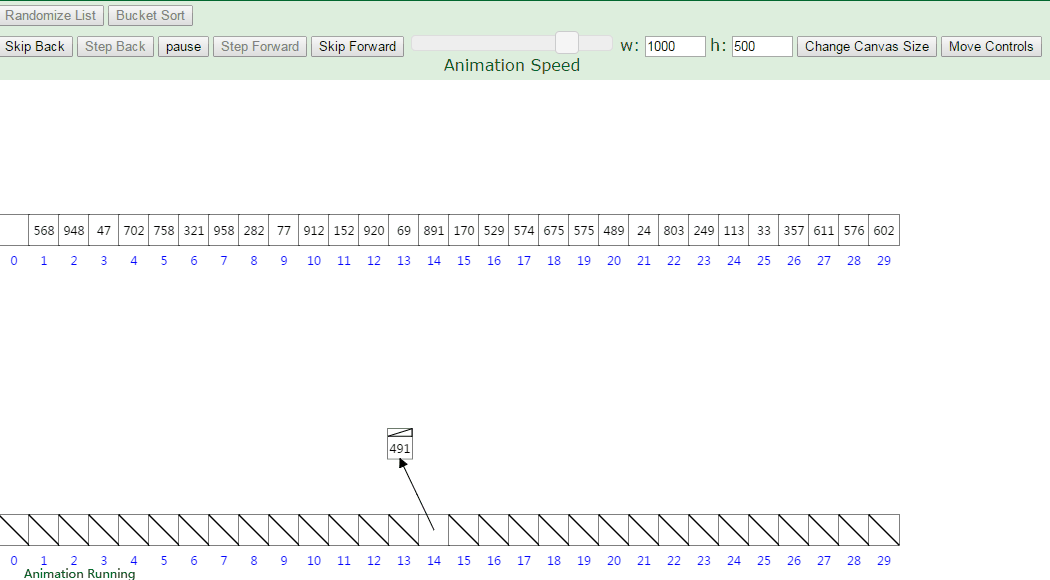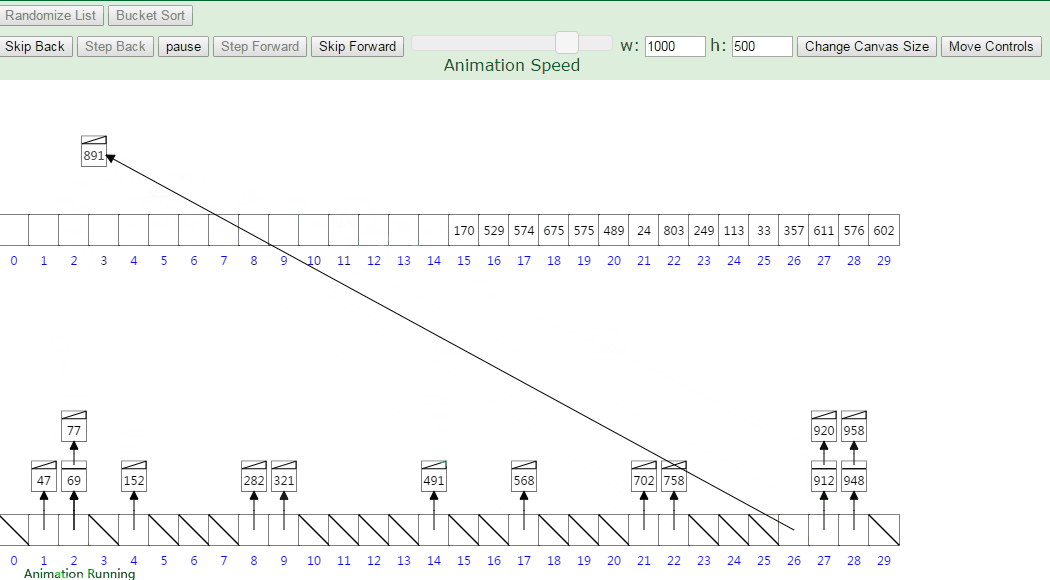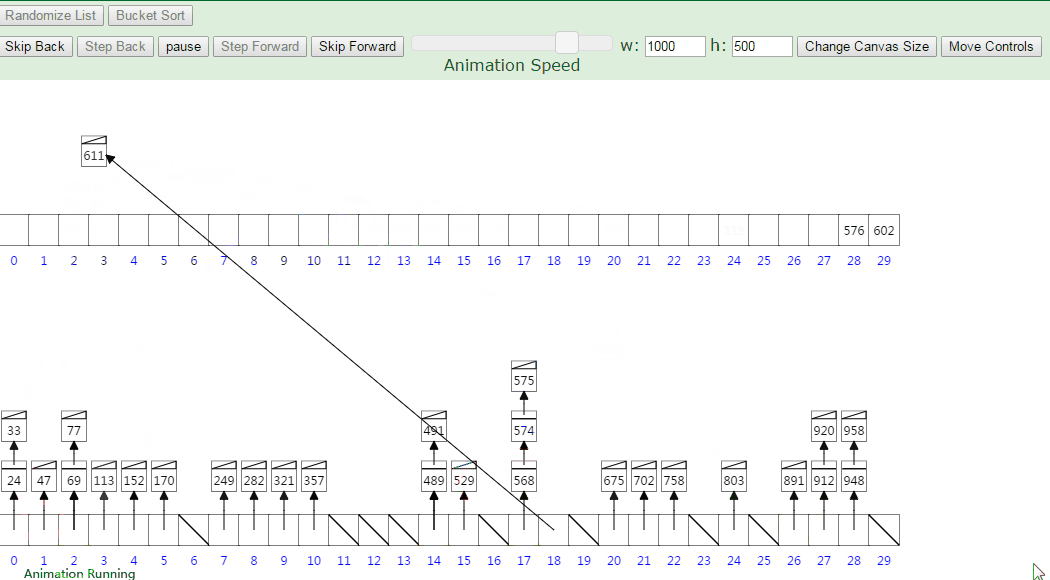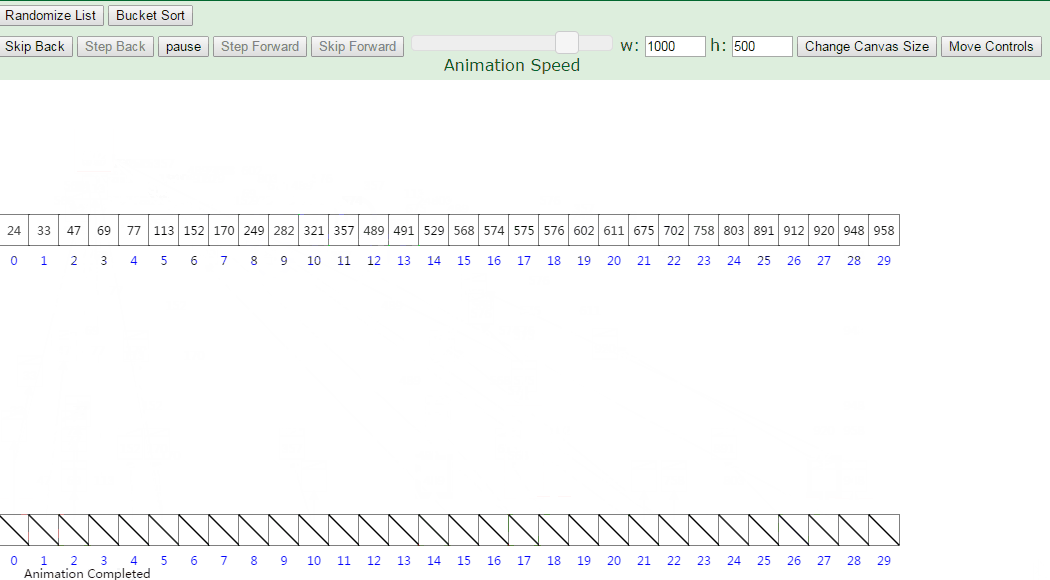
10、桶排序
要求:数组的每个元素的位数必须相同
原理 :
桶排序的思想近乎彻底的分治思想。同样类似于计数排序。
桶排序假设待排序的一组数 均匀独立的分布在一个范围中 ,并将这一范围划分成几个子范围(桶)。然后基于某种映射函数f ,将待排序列的关键字 k 映射到第i个桶中 (即桶数组B 的下标i) ,那么该关键字k 就作为 B[i]中的元素 (每个桶B[i]都是一组大小为N/M 的序列 )。
接着将各个桶中的数据有序的合并起来 : 对每个桶B[i] 中的所有元素进行比较排序 (可以使用快排)。然后依次枚举输出 B[0]….B[M] 中的全部内容即是一个有序序列。
补充: 映射函数一般是 f = array[i] / k; k^2 = n; n是所有元素个数
为了使桶排序更加高效,我们需要做到这两点:
在额外空间充足的情况下,尽量增大桶的数量
使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中
同时,对于桶中元素的排序,选择何种比较排序算法对于性能的影响至关重要。
代码实现:
public static double[] bucketSort(double arr[], int bucketCount) {
int len = arr.length;
double[] result = new double[len];
double min = arr[0];
double max = arr[0];
//找到最大值和最小值
for (int i = 1; i < len; i++) {
min = min <= arr[i] ? min: arr[i];
max = max >= arr[i] ? max: arr[i];
}
//求出每一个桶的数值范围
double space = (max - min + 1) / bucketCount;
//先创建好每一个桶的空间,这里使用了泛型数组
ArrayList < Double > [] arrList = new ArrayList[bucketCount];
//把arr中的数均匀的的分布到[0,1)上,每个桶是一个list,存放落在此桶上的元素
for (int i = 0; i < len; i++) {
int index = (int) Math.floor((arr[i] - min) / space);
if (arrList[index] == null) {
//如果链表里没有东西
arrList[index] = new ArrayList < Double > ();
arrList[index].add(arr[i]);
} else {
//排序
int k = arrList[index].size() - 1;
while (k >= 0 && (Double) arrList[index].get(k) > arr[i]) {
if (k + 1 > arrList[index].size() - 1) {
arrList[index].add(arrList[index].get(k));
} else {
arrList[index].set(k + 1, arrList[index].get(k));
}
k--;
}
if (k + 1 > arrList[index].size() - 1) {
arrList[index].add(arr[i]);
} else {
arrList[index].set(k + 1, arr[i]);
}
}
}
//把各个桶的排序结果合并 ,count是当前的数组下标
int count = 0;
for (int i = 0; i < bucketCount; i++) {
if (null != arrList[i] && arrList[i].size() > 0) {
Iterator < Double > iter = arrList[i].iterator();
while (iter.hasNext()) {
Double d = (Double) iter.next();
result[count] = d;
count++;
}
}
}
return result;
}
//开始排序,其中arr为需要排序的数组
double[] result = bucketSort(arr,bucketCount);参考链接:
总结

疑问:计数排序与基数排序为什么要逆序遍历赋值,原因何在????????????????
若有不足,请多指教,定当洗耳恭听。





















