粒子群算法( Particle Swarm Optimization, PSO)最早是由Eberhart和Kennedy于1995年提出,它的基本概念源于对鸟群觅食行为的研究。鸟群中有个体和群体,个体和群体的信息是可以互通的。个体在随机搜寻食物的过程中,只要跟踪离食物最近的群体,就能最有效地找到食物。
1.一些基本概念
(1)粒子:优化问题的候选解,指鸟群中的一个个个体;
(2)位置:候选解所在的位置,即鸟群个体的位置;
(3)速度:粒子的移动速度;
(4)适应度:评价粒子优劣的值,一般为优化目标函数的数值;
(5)个体极值:单个粒子迄今为止找到的最佳位置,就鸟群觅食而言,是单个个体能够发现距离食物最近的个体;
(6)群体极值:所有粒子迄今为止找到的最佳位置。
2.大概流程及经典公式
根据这些概念,可以大概知道流程:1)初始粒子;2)计算适应度值;3)定义初始个体极值与群体极值;4)更新粒子位置与速度;5)更新个体极值和群体极值。
在实际问题的解决中,构建目标函数是最重要的,也是最难的。而粒子群算法中最经典的部分在于步骤4)(更新粒子位置与速度),其公式如下:
图1
xid——粒子的位置;
vid——粒子的移动速度;
w——惯性权重;
c1,c2——学习因子;
r1,r2——[0.1]中的随机数;

标准PSO算法的核心公式如下:


其中,w,c1,c2是预置好的:
w称为惯性权重,大小一般在[0.5,1.5]。
c1,c2称为学习因子,一般取值[1,4],通常设置的c1=c2,但是c1与c2不必完全相同。
此实验是在二维空间寻找最小值,设置多峰函数:
z = x^2 + y-7cos(pix)-8cos(2pi*y);
它的图像如下所示,我们要找的是z的最小值,也是z轴的最低点。

下面是一些参数设置的变化对粒子收敛情况的影响
本次实验中,种群规模为100,迭代次数为100,其他参数进行不断的变化
(1)w=0.8 , c1=1.4 , c2=1.4 这是一般情况下参数的设置。
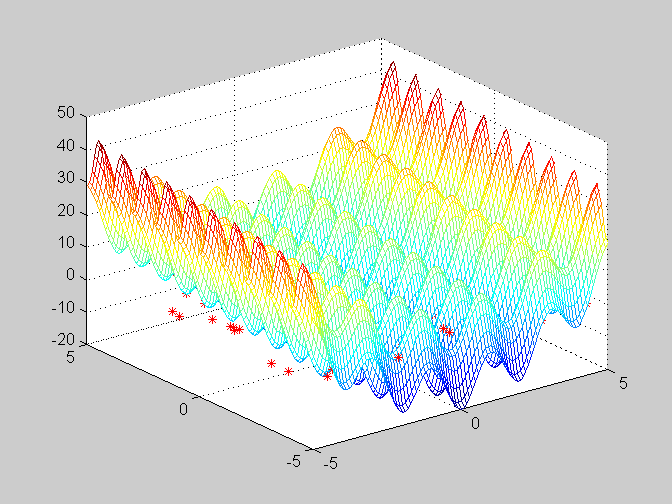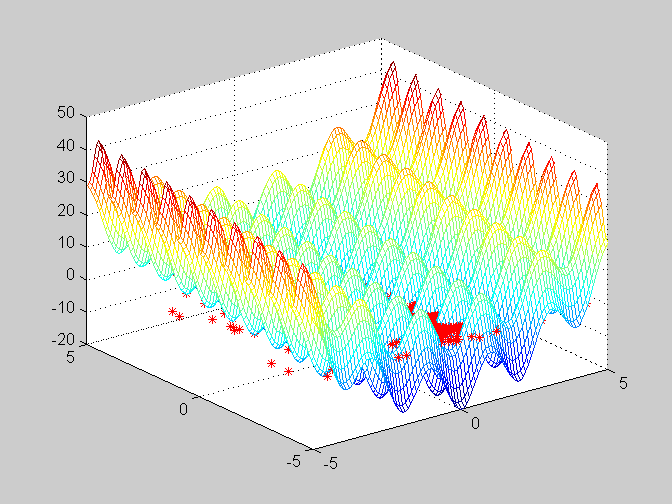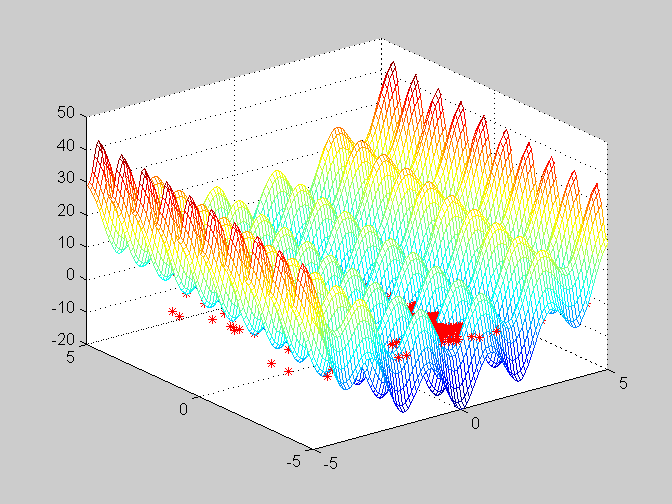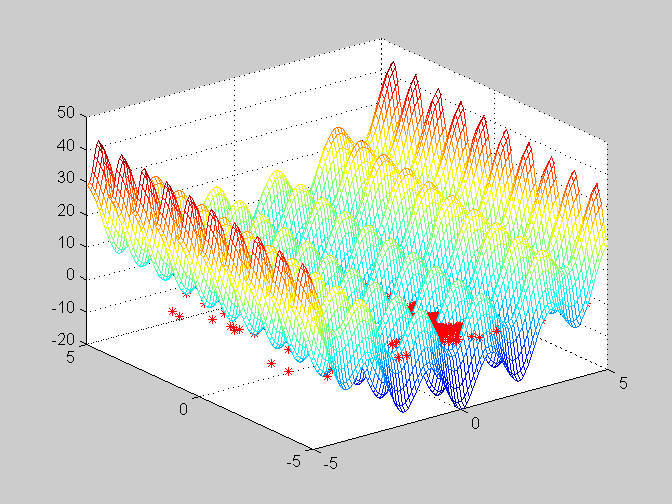
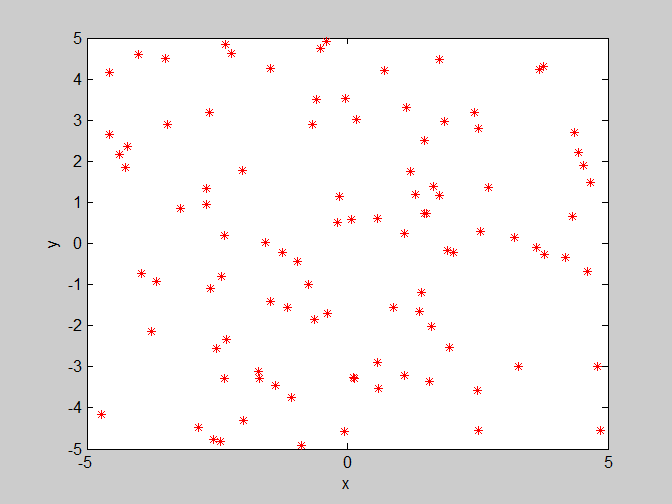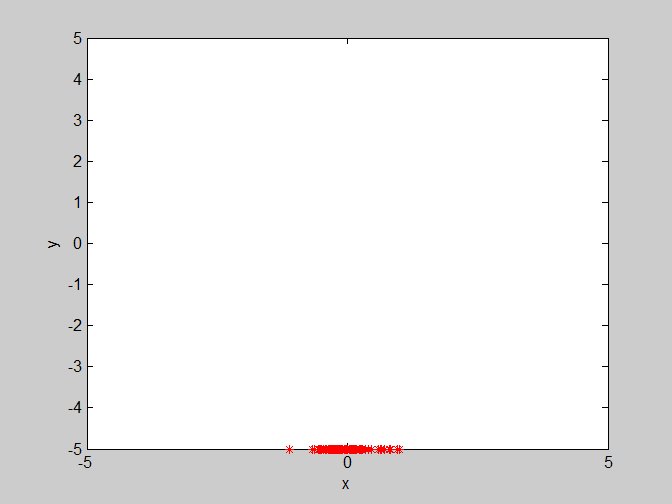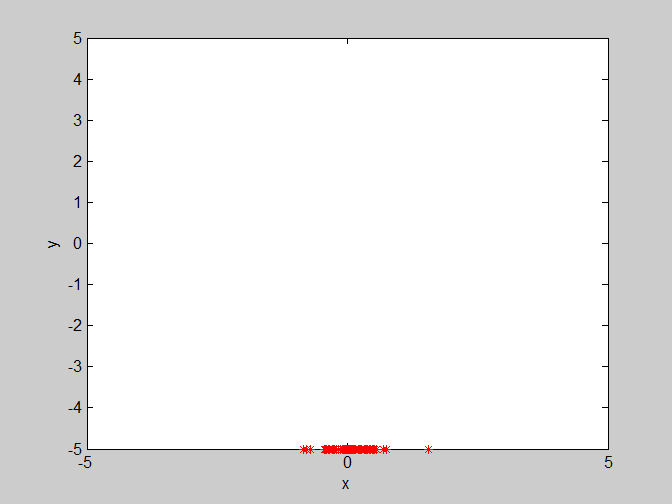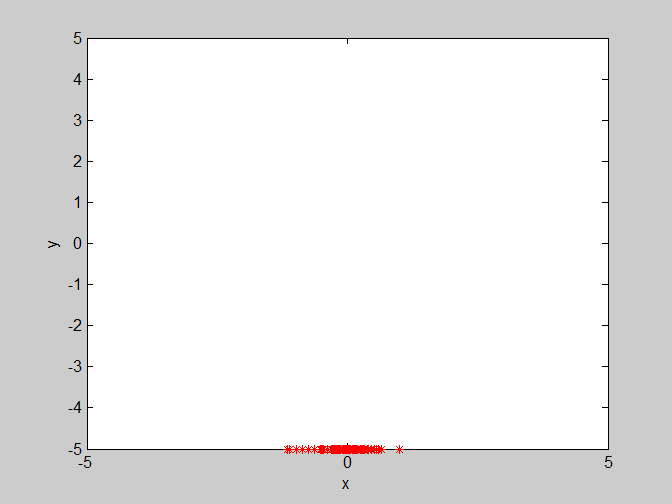
上图是粒子群在三维图上的变化,可以看出粒子的分布越来越集中,由于寻找的是最小值,后期的分布很难看出,以下是x-y的一个俯视图,看出粒子越来越集中。

后面为了更加直观的了解粒子的收敛情况,只给出粒子在二维平面(x,y)的一个运动情况。
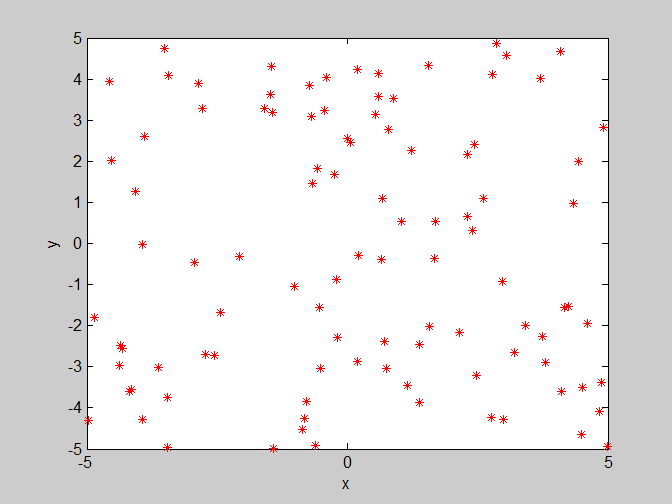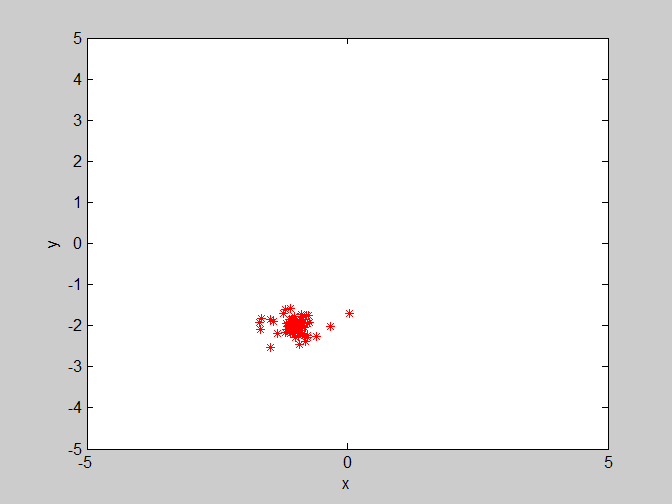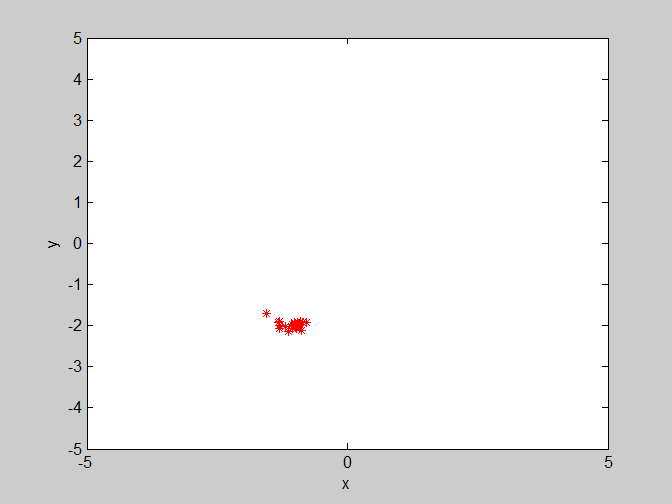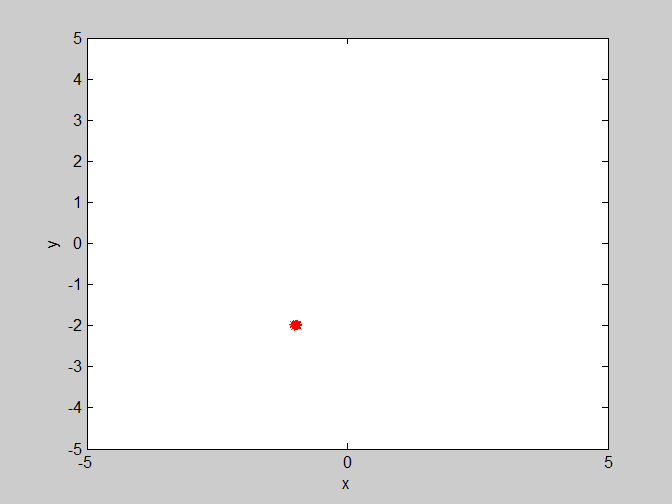
(2)w=1.2 , c1=1.4 , c2=1.4 惯性权重变大,使得粒子对上一代的速度继承了更多,可能会导致粒子收敛困难。
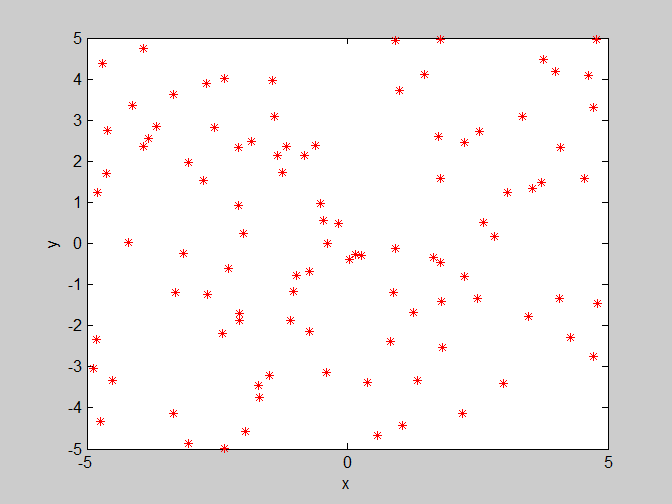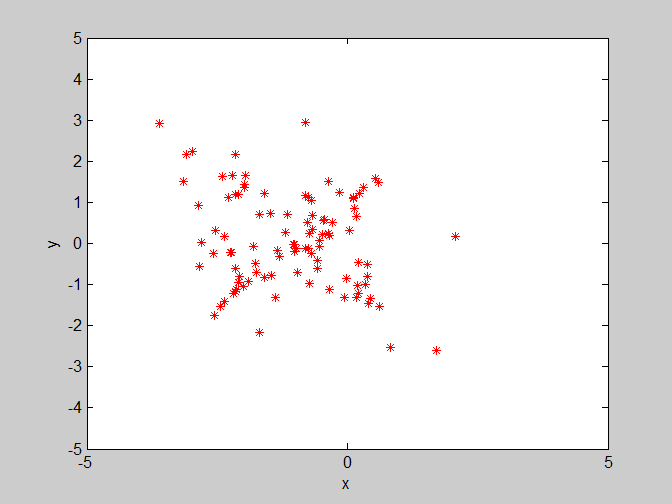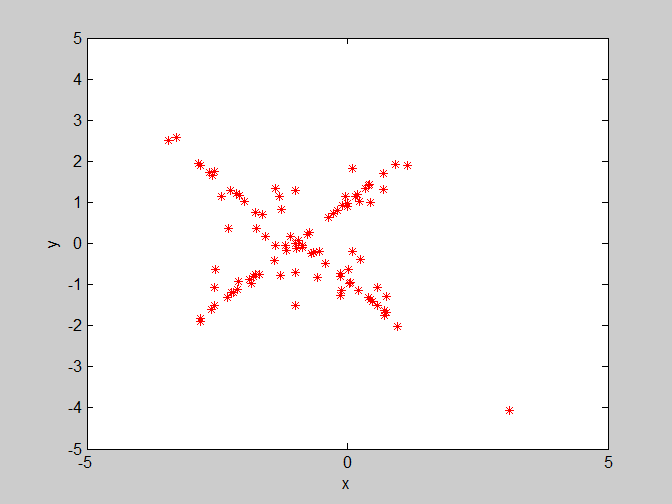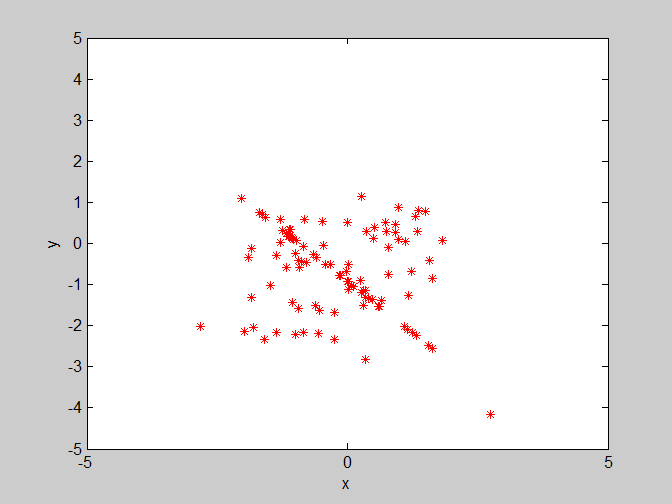
(3)w=0.8 , c1=3 , c2=1.4。这里将w继续设置为0.8,个体学习因子c1变大,对收敛会有部分影响,通过多次实验发现它会导致最终寻找的最优解的变化范围变大。
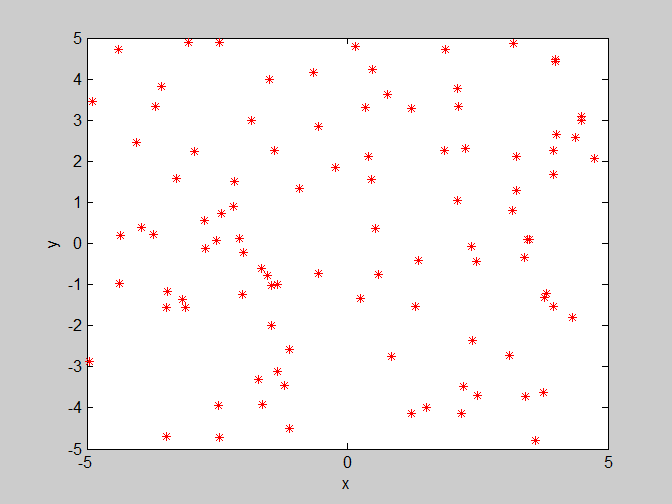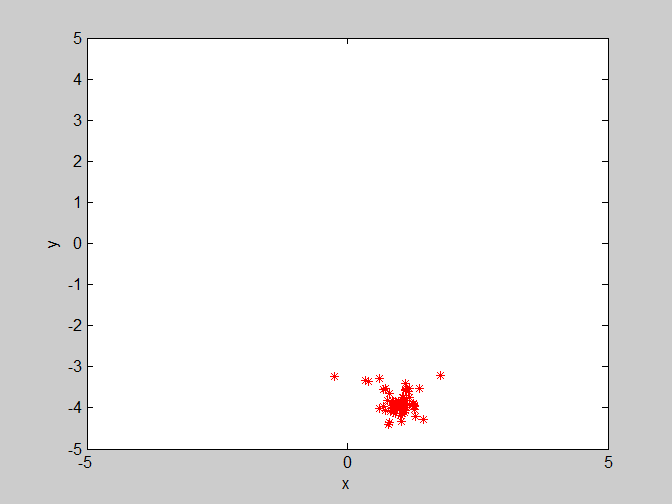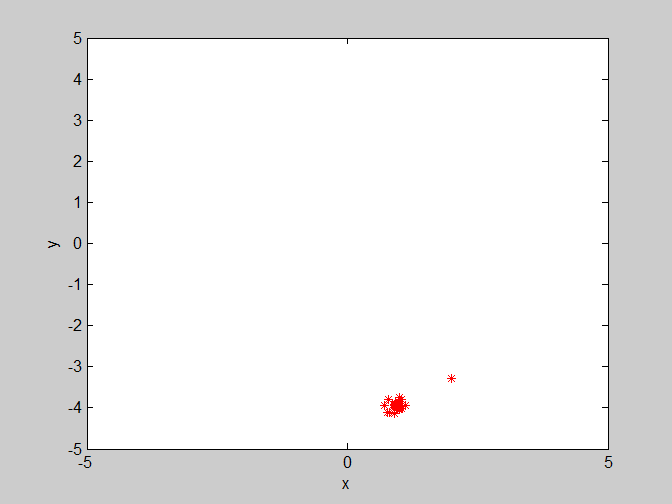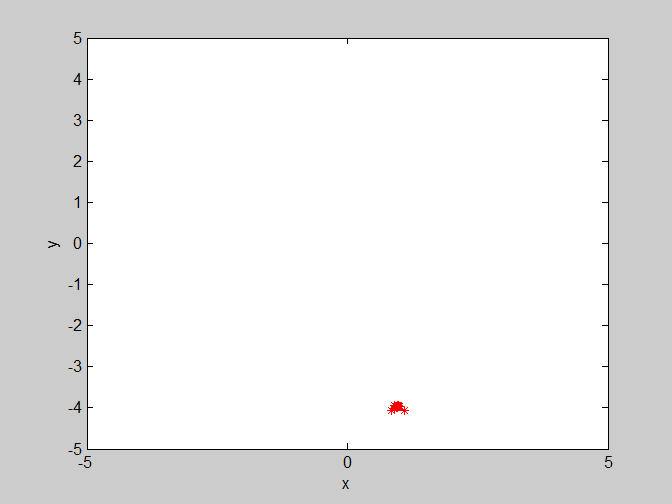
(4)w=0.8 , c1=1.4 , c2=3。群体学习因子c2变大,对收敛会有部分影响,但是影响程度没有w剧烈。
结论:
1.c1的值如果较大会缺乏搜索指导,虽然有时会得到最优解,但实验的结果随机性过大。
2.c2的值如果较大会影响最优值,但影响不大。
3.w的值如果较大会让粒子迅速拉向目标区域或者越过目标区域,进而影响算法性能。
4.对算法性能影响最大的是惯性权重,其次是加速系数。
5. 在种群规模不太小的情况下,适当的增加迭代次数会使结果更优。
改进:
1.初始使用较大的c1值和较小的c2值,增加多样性,后期让c1的值线性降低,c2的值线性增加,增强粒子收敛能力。
2.w的值在前期设置较大有助于全局搜索,后期减小加强局部搜索。





















