java冒泡排序升序代码 java冒泡排序代码及解释

一、冒泡排序

1、排序说明

冒泡排序（Bubble Sort），是一种计算机科学领域的较简单的排序算法。
它重复地走访过要排序的元素列，依次比较两个相邻的元素，如果顺序（如从大到小、首字母从Z到A）错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换，也就是说该元素列已经排序完成。
这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端（升序或降序排列），就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样，故名“冒泡排序”。

2、代码示例

arr[i] < arr[j] 表示 i 的值 小于 j 的值，就进行交换， i 为外层for循环，此排序为升序

arr[i] > arr[j] 表示 i 的值 大于 j 的值，就进行交换， i 为外层for循环，此排序为降序

每走完异常外层的 for 循环排序后 ,i 索引的值都为最大值

/**
     * TODO   冒泡排序
     */
    @Test
    public void MpSort() {
        long[] arr = {2, 4, 3, 5, 1};
        for (int i = 0; i < arr.length; i++) {
            for (int j = 0; j < arr.length; j++) {
                long item;
                if (arr[i] < arr[j]) {
                    item = arr[i];
                    arr[i] = arr[j];
                    arr[j] = item;
                    System.out.println("排序索引:" + i + " --> " +Arrays.toString(arr));//查看每次排序后内容
                }
            }
        }
    }

3、执行流程

比较相邻的元素。如果第一个比第二个大，就交换他们两个。 [1]

对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。 [1]

针对所有的元素重复以上的步骤，除了最后一个。 [1]

持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。 [1]

4、动图演示

二、 选择排序（基于冒泡排序）

1、排序说明

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理是：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。

选择排序是一种简单直观的排序算法，无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。

2、代码示例

for ( j = min --> 表示剩余未排序元素中继续寻找最小（大）元素
if(min != i) --> 表示避免性能浪费，当 min 和 i 相同时,不进行值的替换
arr[j] < arr[min] --> 表示升序

/**
     * TODO   选择排序
     */
    @Test
    public void KsSort() {

        long[] arr = {2, 4, 3, 5, 1};

        for (int i = 0; i < arr.length; i++) {
            int min = i;
            // j = min, 表示剩余未排序元素中继续寻找最小（大）元素
            for (int j = min; j < arr.length; j++) {
                if (arr[j] < arr[min]) {
                    min = j;
                }
            }
            // 避免性能浪费，当 min 和 i相同时,不进行值的替换
            if (min != i) {
                long item = arr[i];  //保存索引i的值
                arr[i] = arr[min];   //索引i 赋值为 最小值
                arr[min] = item;     //最小值的索引 赋值为 索引i的之前的值
            }

            System.out.println("排序索引:" + i + " --> " +Arrays.toString(arr));//查看每次排序后内容
        }
    }

3、执行流程

首先在未排序的序列中找到最小（大）元素，存放到排序序列的起始位置。再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。重复第二步，直到所有元素均排序完毕。

当前代码为 long[] arr = {2, 4, 3, 5, 1}; 实际替换过程如下

4、动图演示

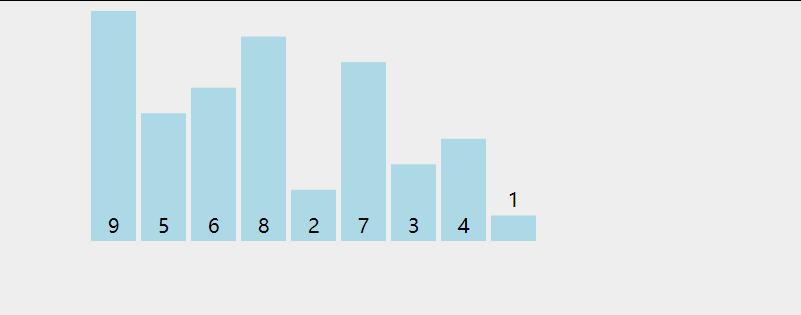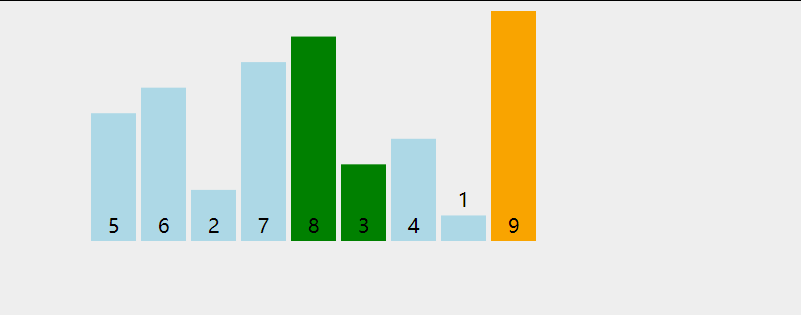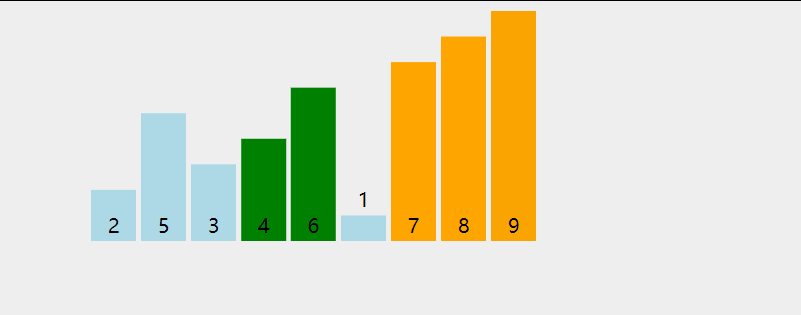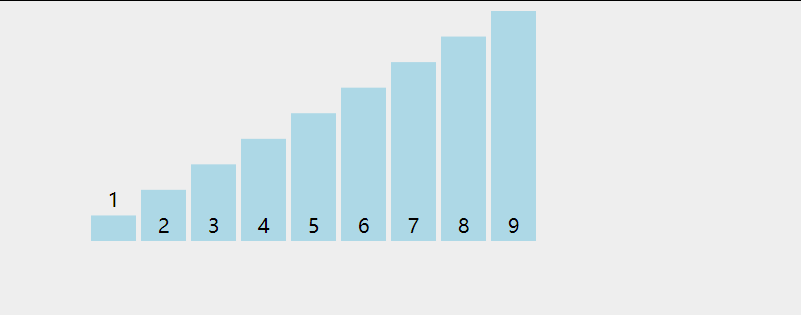
三、 插入排序

1、排序说明

插入排序，一般也被称为直接插入排序。对于少量元素的排序，它是一个有效的算法 [1] 。插入排序是一种最简单的排序方法，它的基本思想是将一个记录插入到已经排好序的有序表中，从而一个新的、记录数增1的有序表。在其实现过程使用双层循环，外层循环对除了第一个元素之外的所有元素，内层循环对当前元素前面有序表进行待插入位置查找，并进行移动

插入排序的工作方式像许多人排序一手扑克牌。开始时，我们的左手为空并且桌子上的牌面向下。然后，我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置，我们从右到左将它与已在手中的每张牌进行比较。拿在左手上的牌总是排序好的，原来这些牌是桌子上牌堆中顶部的牌

2、代码示例

遍历所有已插入的数据 arr[i]=当前插入的数据, j = i, 遍历[i-0]
if (j > 0 && temp < arr[j - 1]) 第一个参数不移动, 假设 i = 10，遍历[9-0], 一旦发现 arr[i] < arr[j] , 把 arr[j]的值全部后移一位,

/**
     * TODO   插入排序
     */
    @Test
    public void CrSort() {
      
        long[] arr = {2, 4, 3, 5, 1};
        long temp;
      
        for (int i = 1; i < arr.length; i++) {
            temp = arr[i];
            for (int j = i; j >= 0; j--) {
                if (j > 0 && temp < arr[j - 1]) {
                    arr[j] = arr[j - 1];
                } else {
                    arr[j] = temp;
                    System.out.println("插入索引:" + i + " --> " + Arrays.toString(arr));
                    break;
                }
            }
        }
    }

3、执行流程

4、动图演示

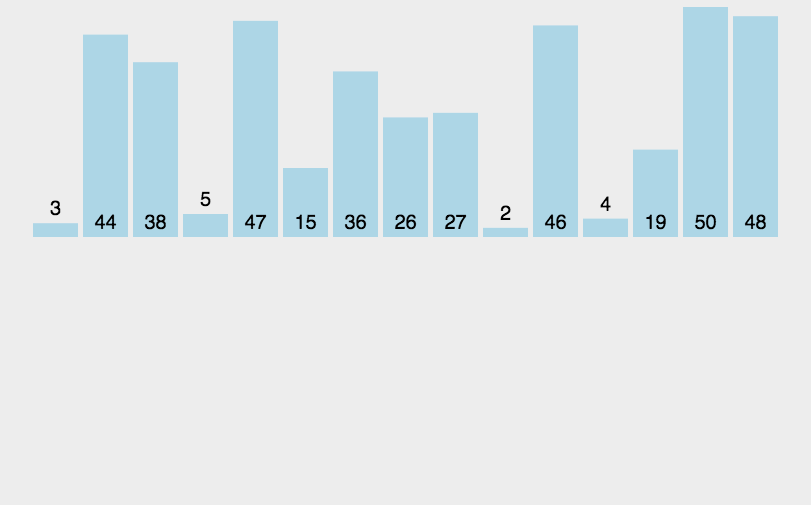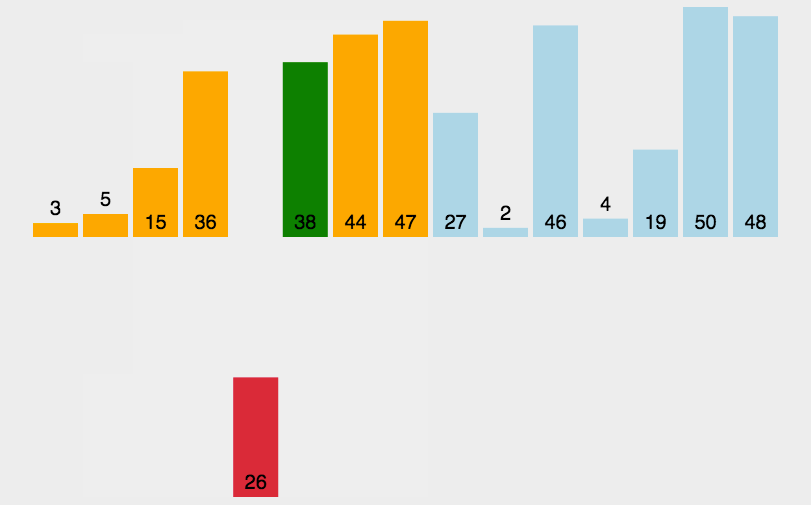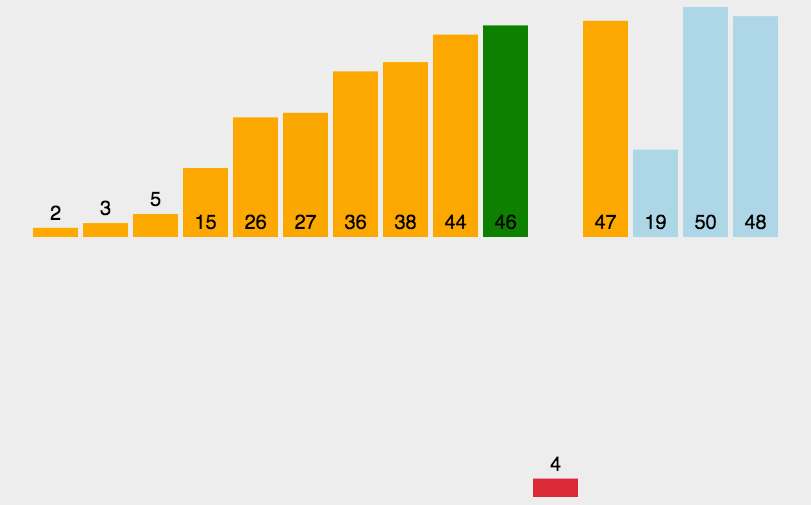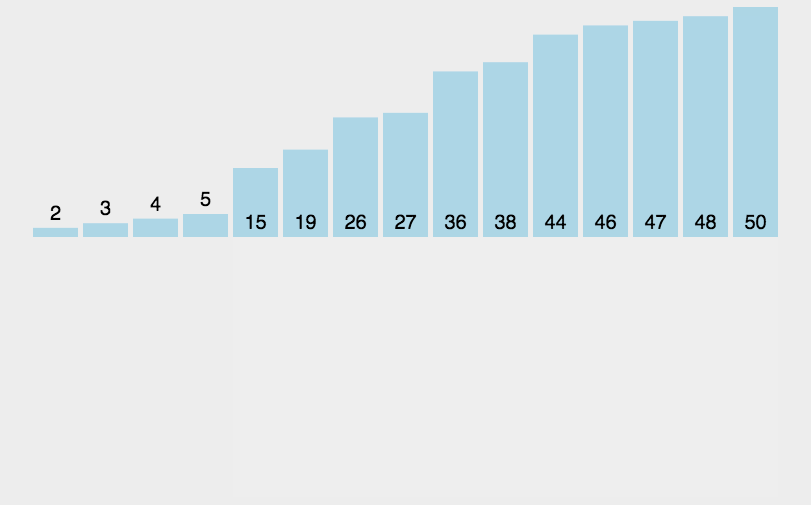
四、希尔排序（基于插入排序）

1、排序说明

1959年Shell发明，第一个突破O(n2)的排序算法，是简单插入排序的改进版。它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。

先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，具体算法描述：

选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
按增量序列个数k，对序列进行k 趟排序；
每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

2、代码示例

package sort;

import java.util.Arrays;

/**
 * TODO  希尔排序
 *
 * @author ws
 * @mail [e-mail]
 * @date 2020/5/30 0030 20:53
 */
public class ShellSort {


    public static void main(String[] args) {
        long[] arr = {2, 4, 3, 5, 1, 6};
        shell_sort(arr, arr.length);
        System.out.println("--- > " + Arrays.toString(arr));
    }


    public static void shell_sort(long arr[], int length) {

        long temp = 0;
        int incre = length;

        while (true) {
            incre = incre / 2;
            for (int k = 0; k < incre; k++) {    //根据增量分为若干子序列
                for (int i = k + incre; i < length; i += incre) {
                    for (int j = i; j > k; j -= incre) {
                        if (arr[j] < arr[j - incre]) {
                            temp = arr[j - incre];
                            arr[j - incre] = arr[j];
                            arr[j] = temp;
                        } else {
                            break;
                        }
                    }
                }
            }
            //
            if (incre == 1) {
                break;
            }
        }
    }
}

3、动图演示

10/2 =5

第一次排序间隔 5 位数比较，如果后者大于前者就进行交换
第二次排序间隔 4 位数比较，如果后者大于前者就进行交换
第三次排序间隔 3 位数比较，如果后者大于前者就进行交换
第四次排序间隔 2 位数比较，如果后者大于前者就进行交换
第五次排序间隔 1 位数比较，如果后者大于前者就进行交换

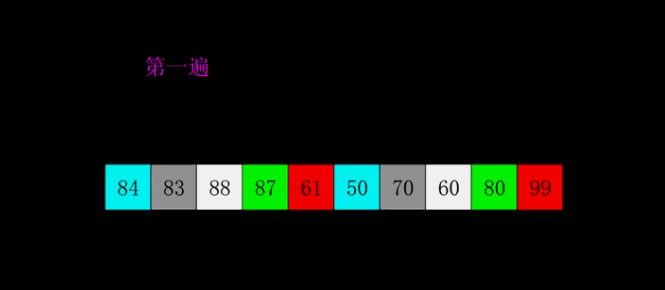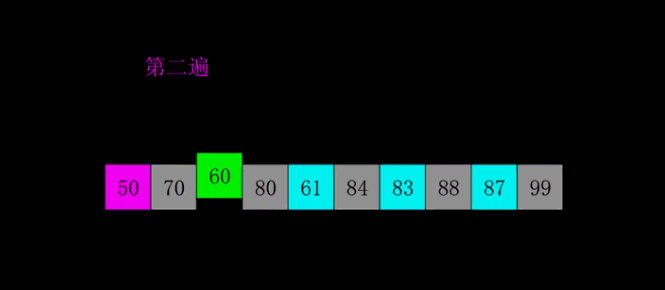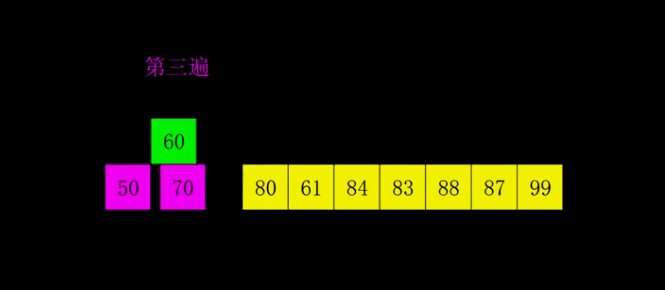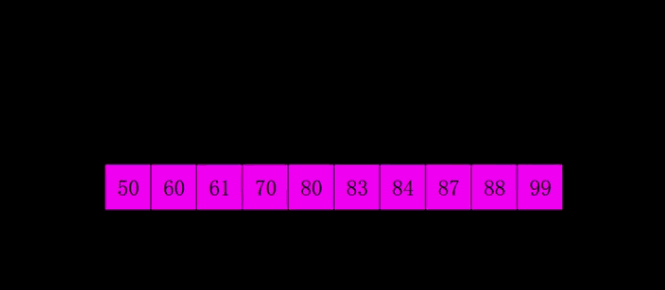
本文到此结束，如果觉得有用，劳烦各位点赞关注一下呗，将不定时持续更新更多的内容…，感谢大家的观看！