【基础算法】单链表的OJ练习(5) # 环形链表 # 环形链表II # 对环形链表II的解法给出证明（面试常问到）

原创

热爱编程的小幸运 2023-06-16 23:07:33 博主文章分类：数据结构与算法 ©著作权

文章标签 环形链表链表算法证明面试题 文章分类 C/C++ 后端开发 yyds干货盘点

©著作权归作者所有：来自51CTO博客作者热爱编程的小幸运的原创作品，请联系作者获取转载授权，否则将追究法律责任

前言

本章的OJ练习相对于OJ练习(4)较为简单。不过，本章的OJ最重要的是要我们证明为何可以这么做。这也是==面试==中常出现的。
对于OJ练习(4)：==->== 传送门 ==<-==，分割链表以一种类似于归并的思想解得，回文链表以一种巧妙复用前面OJ题的思想解得。
啰嗦一下：对于本章，最重要的是需要证明为什么这样做可以，所以我们不光要做出来OJ，还要能够理解并自行给出证明。

环形链表

题目链接： ==->== 传送门 ==<-==。
题目描述：给你一个链表的头节点 head ，判断链表中是否有环。如果链表中存在环，则返回 true 。否则，返回 false 。

带环链表类似于下面这种结构：

是否有环，实际上就是链表的最后一个节点是否指向了链表其中的一个节点，如果有环，我们遍历一遍链表的话，会陷入死循环。那么我们该如何判断链表是否有环呢？

解题思路：

由于带环链表直接遍历会陷入死循环，也就是说会无限在环内遍历下去，因此，这里可以引出一个追击问题：用快慢指针遍历链表。
我们定义两个指针，分别是慢指针slow，快指针fast，这两个指针同时遍历链表，slow每次走一步，fast每次走两步。fast会先进入环然后在环内跑圈，当slow进入环后，这就是一个典型的追及问题了，slow每次在环内走一步，fast每次在环内走两步，两个指针的距离每次缩小1，最终fast会追上slow与slow指向同一节点。当两个指针相等时，就可以判断该链表带环，因此判断条件就是fast == slow (return true)。
如果链表不带环，fast最终会指向NULL的前一个结点或者就指向NULL。因此，整个判断过程就结束了。

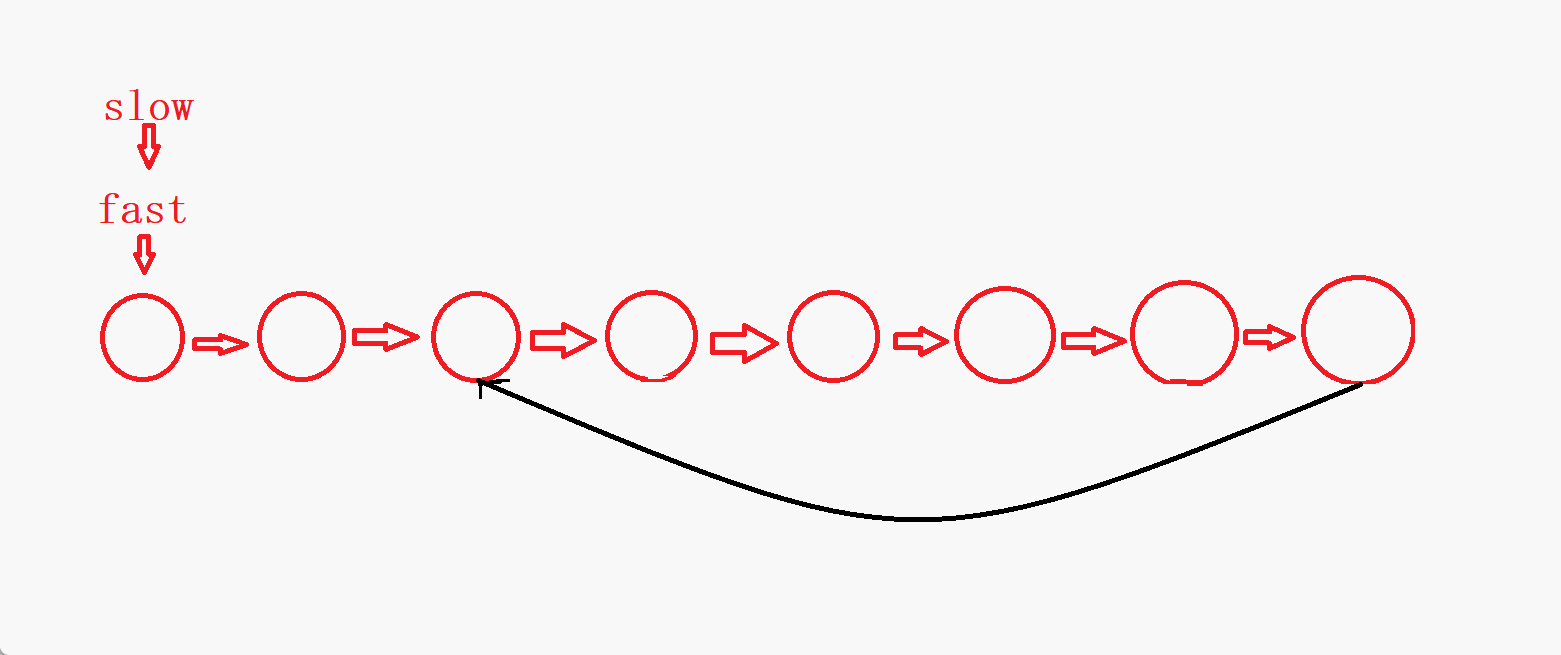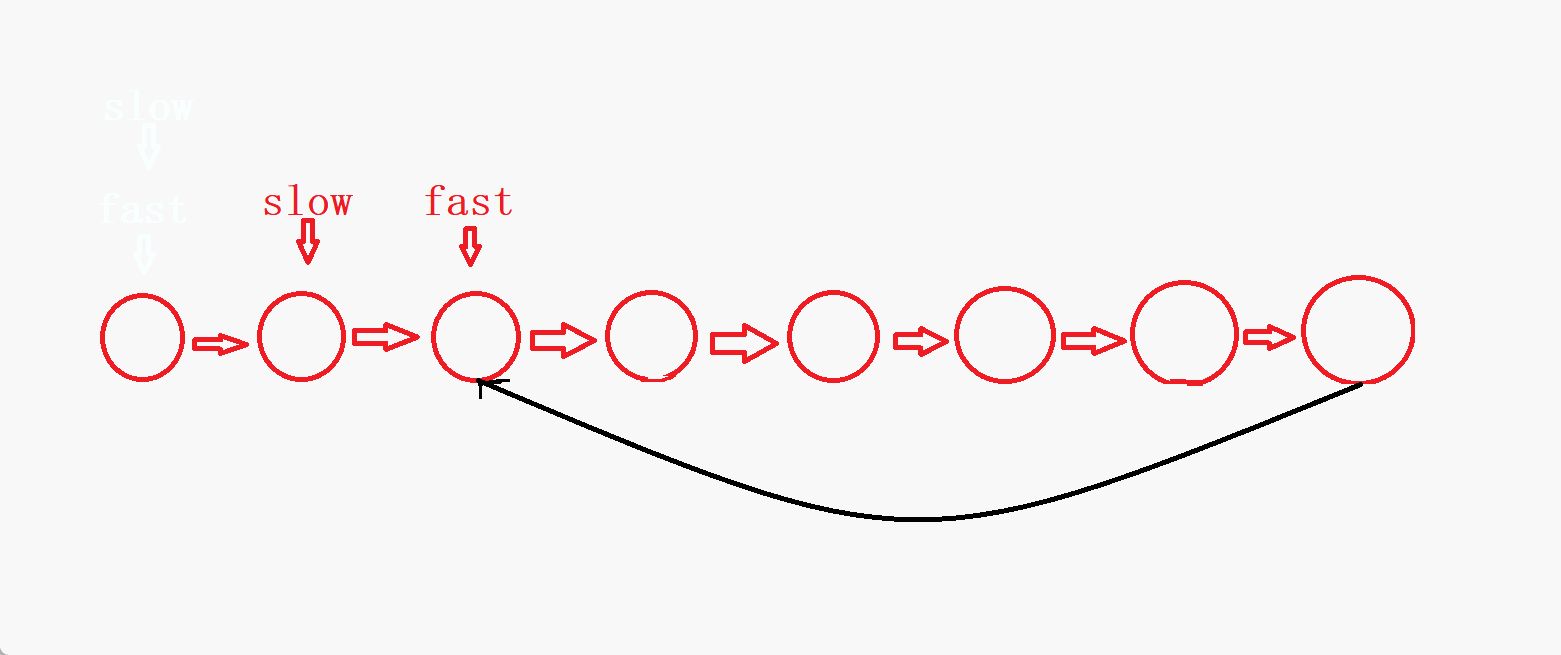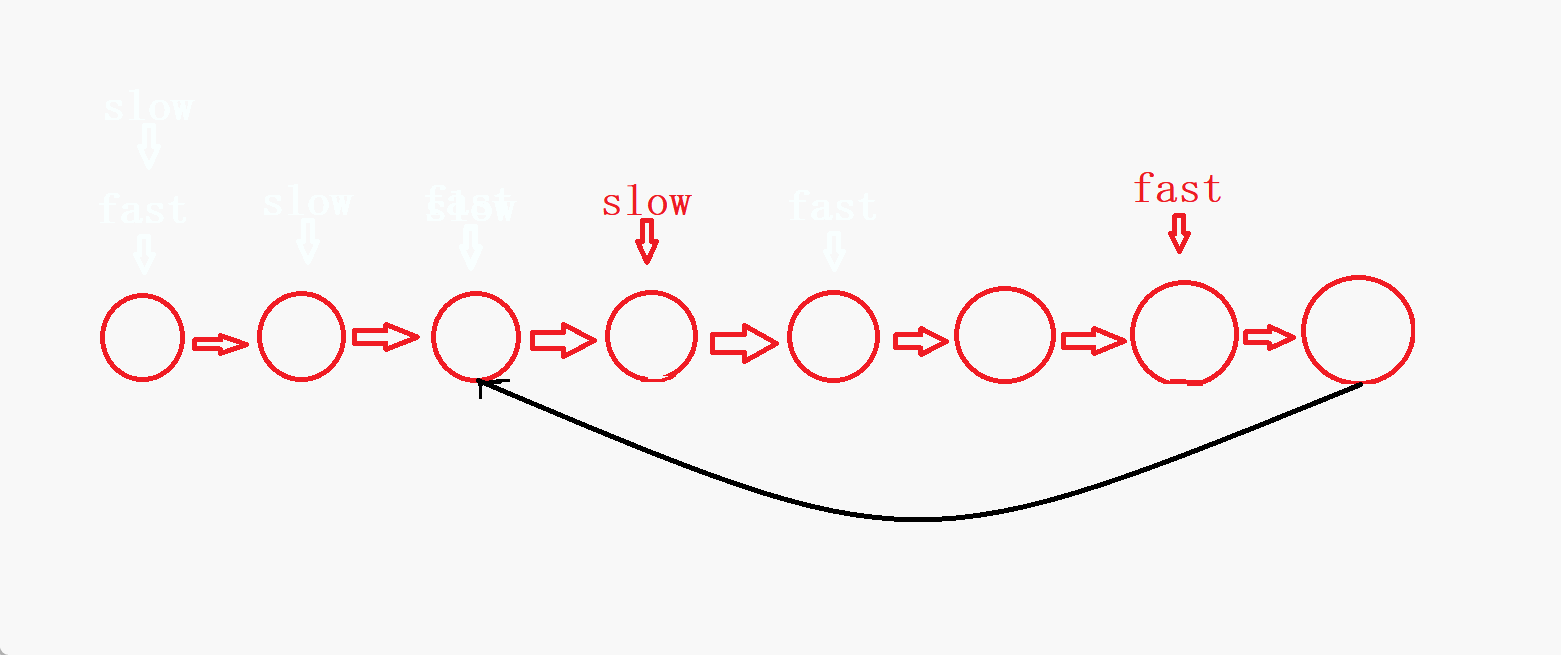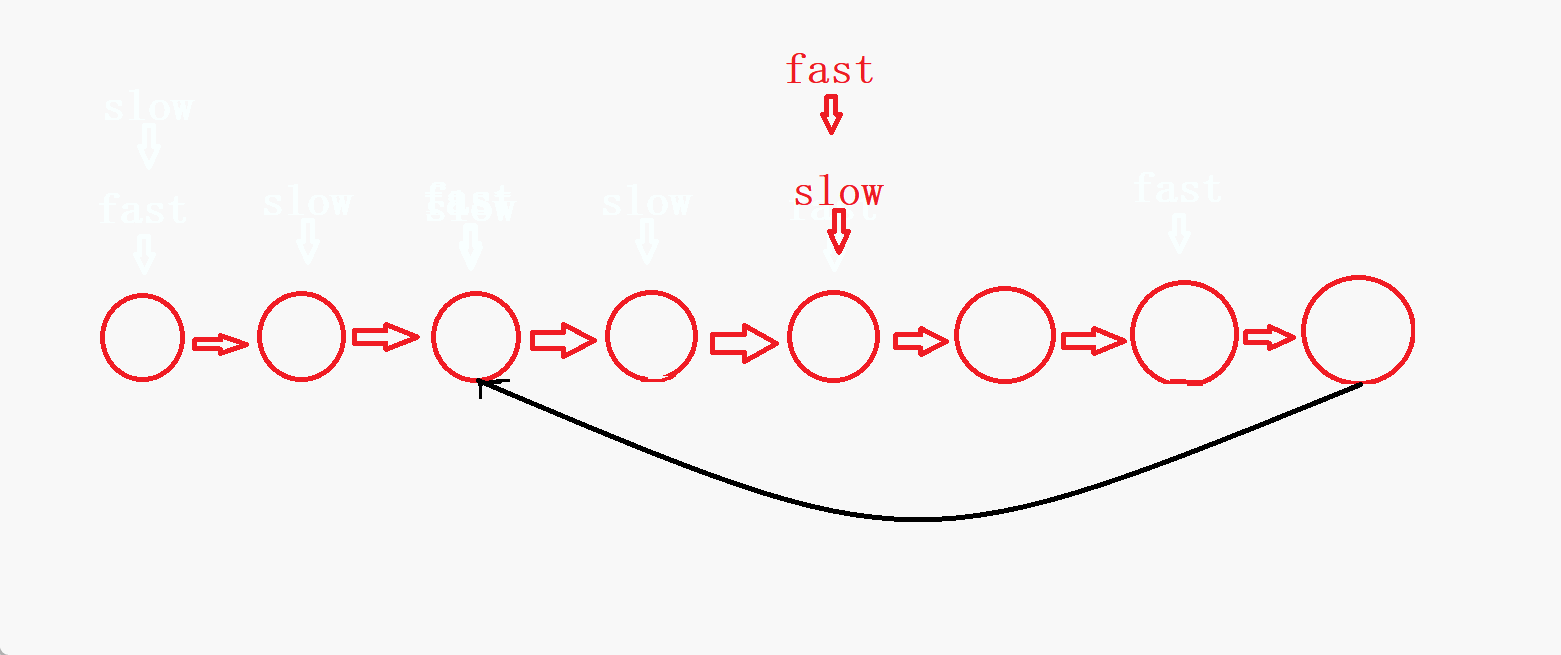
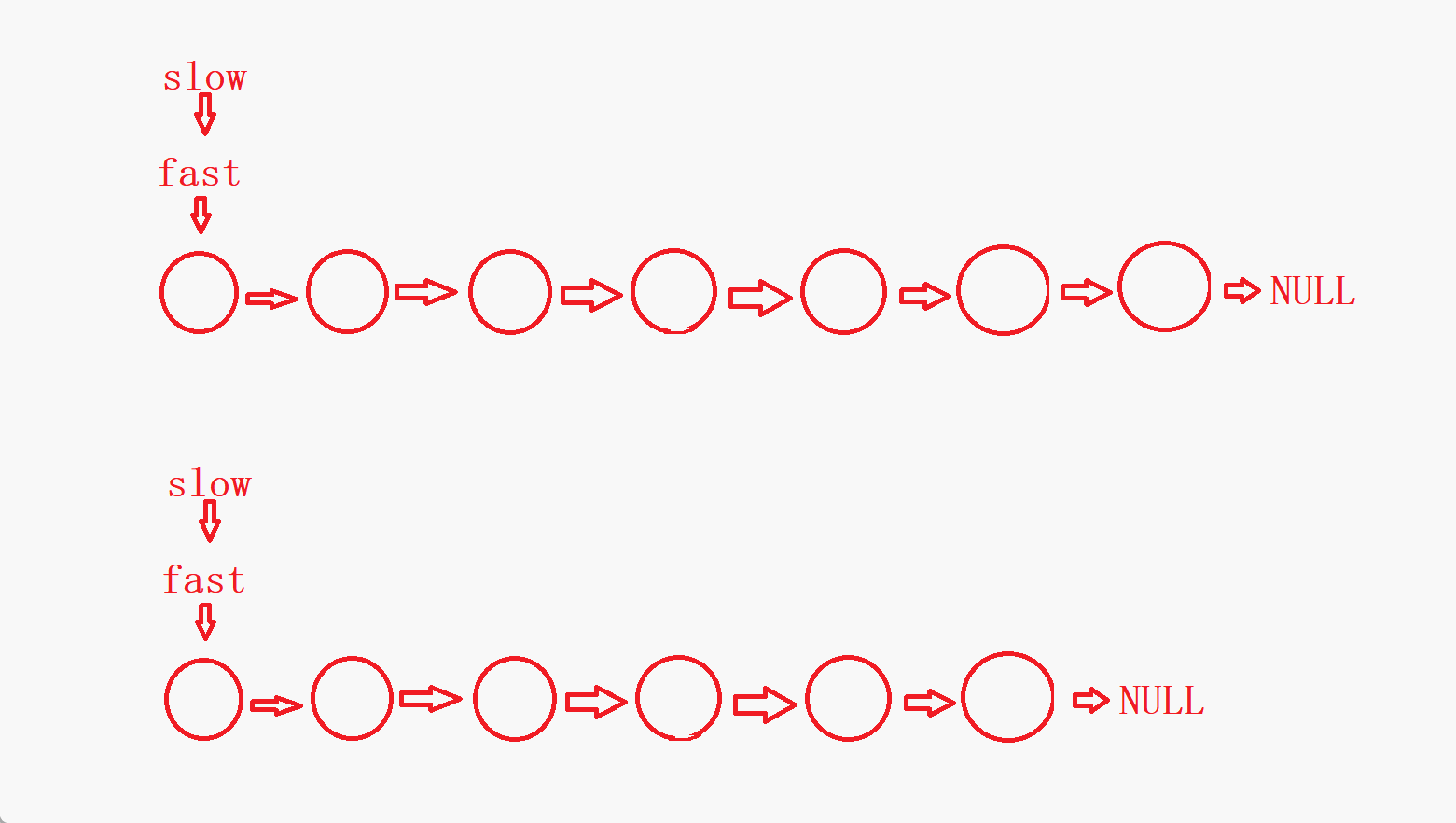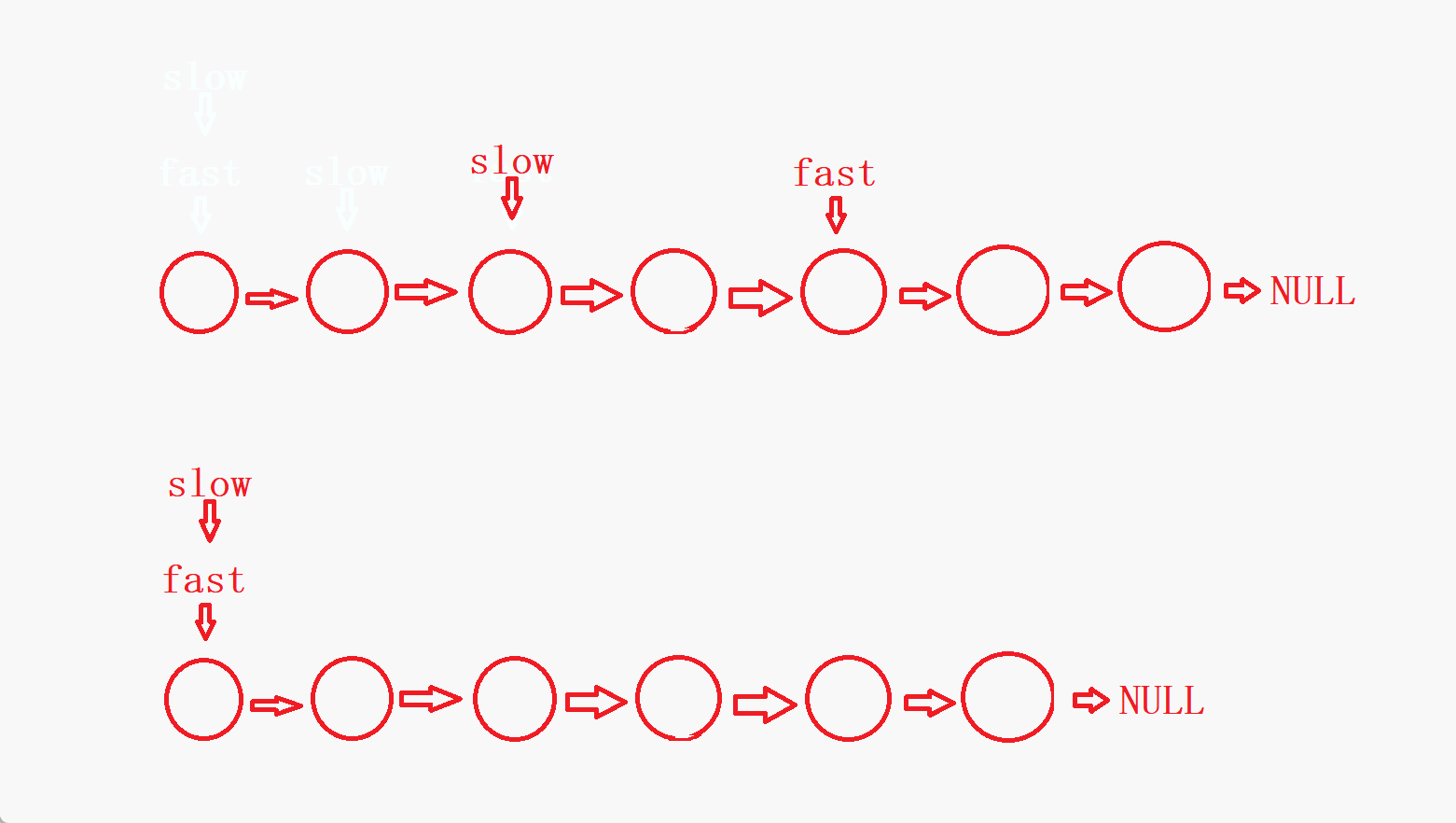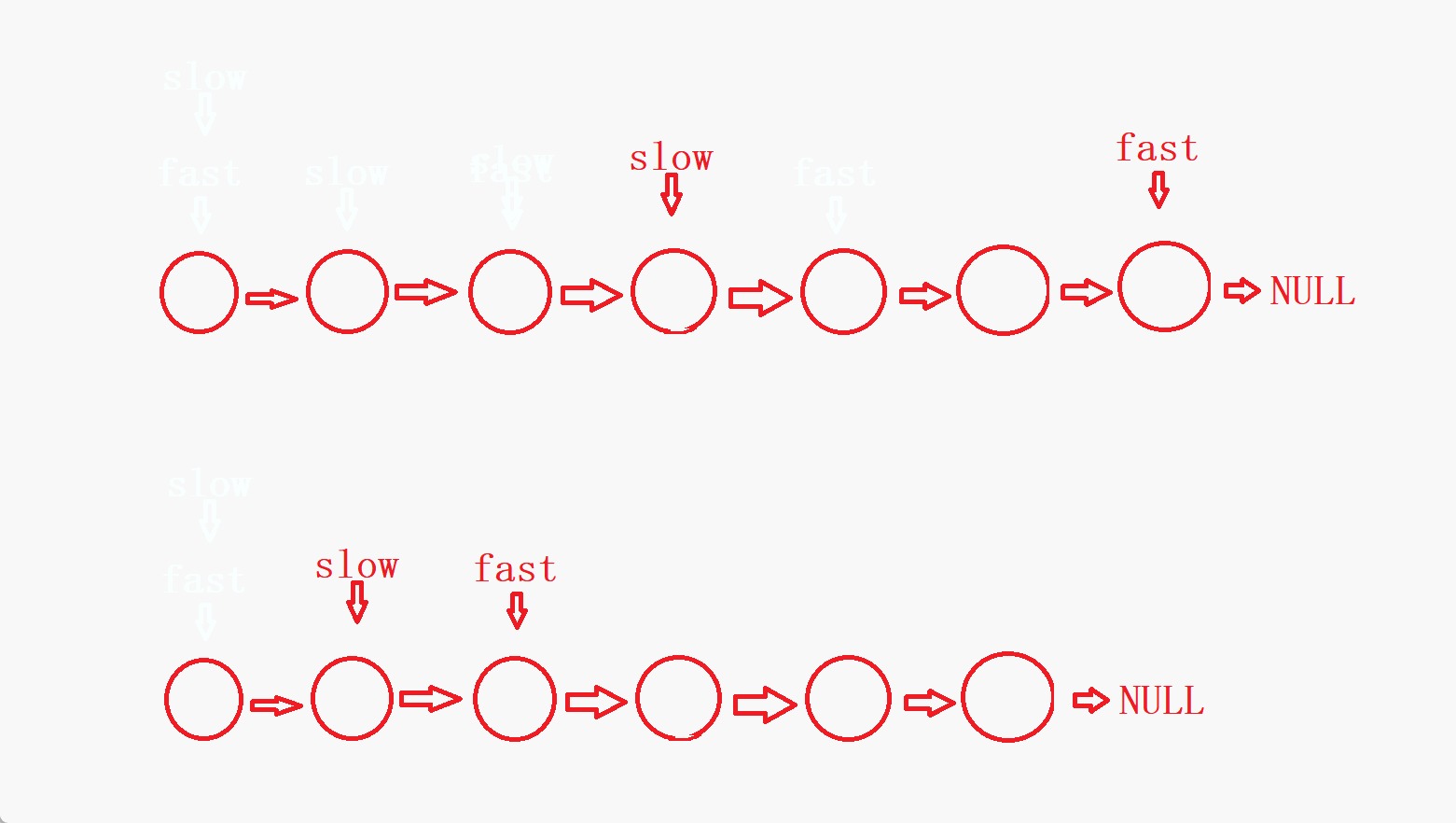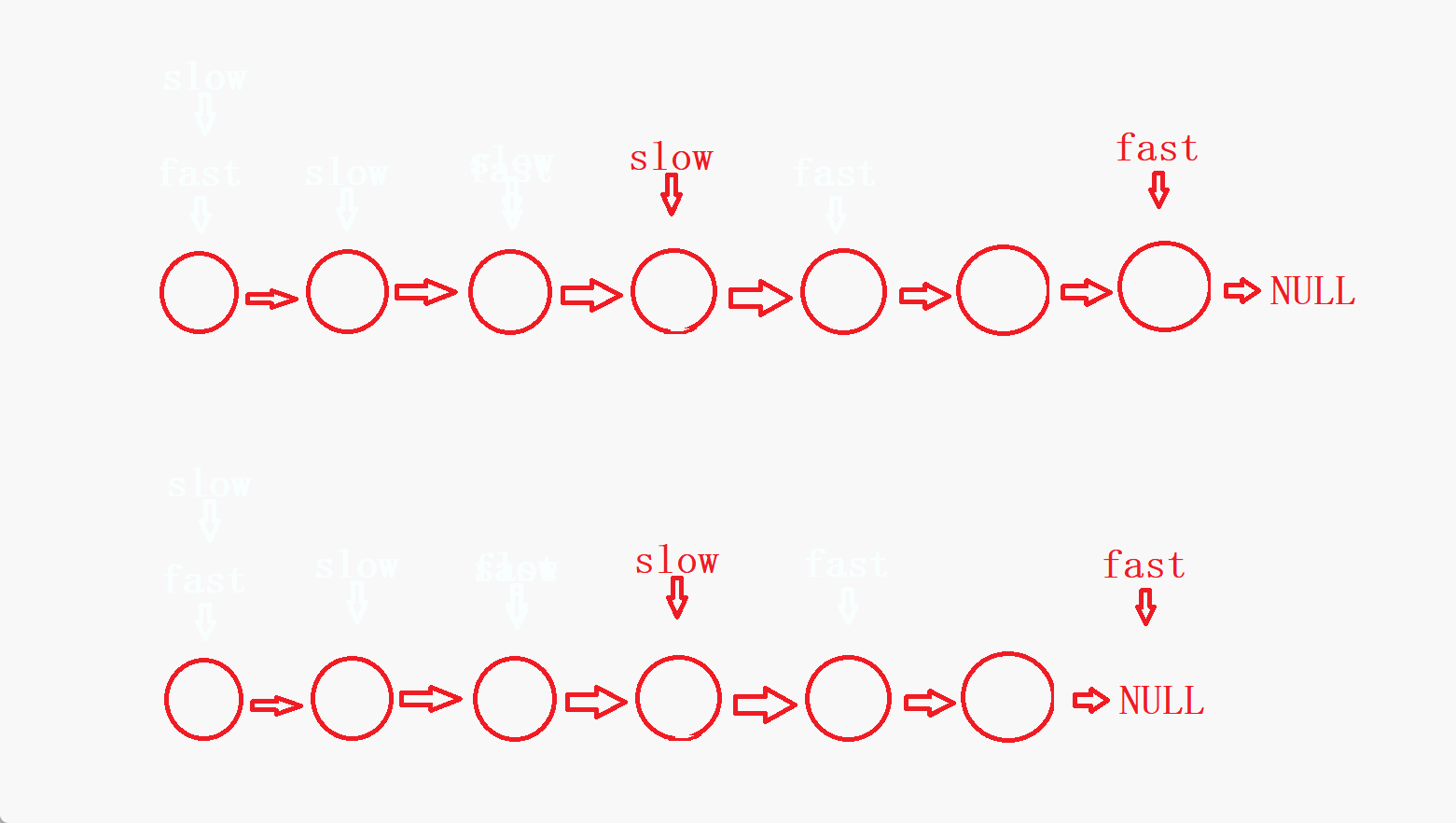
在这里插入图片描述

可以看到，如果链表没有环，链表的结点个数为偶数时，fast是指向NULL结束，链表的节点个数为奇数时，fast是指向最后一个结点结束。

解题代码：

bool hasCycle(struct ListNode *head) {
    struct ListNode* fast = head, * slow = head;

    while (fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;

        if (fast == slow) return true;
    }

    return false;
}

为什么快慢指针可以？

快指针每次走两步，慢指针每次走一步，当两个指针都在环内的时候，就成了一个追击问题，两个指针的距离每次缩小一，最终快指针会追上慢指针，因此判断其有环。
那假如快指针每次走三步，慢指针走一步呢？

我们将带环链表抽象成下图：

在这里插入图片描述假设每次快指针走三步，慢指针每次走一步，当两个指针都进环后，此时的相对位置为：

在这里插入图片描述我们记此时慢指针slow与快指针fast的距离为N，慢指针每次走一步，快指针每次走三步，因此N每次减少2，于是就有：

N - 2 N - 4 N - 6 N - 8 ..... 最终有两种情况： :). N = 1，然后再减2 ==->== -1 ;). N = 2，然后再减2 ==->== 0

如果N最后减为-1，那么再次追击，如果N最后减为0，则快指针等于慢指针，判断为true。所以得出：当N为奇数时，追不上；当N为偶数时，一定追得上。
如果追不上，最后fast会在slow的下一个位置，然后继续追击，那么，继续追击又是否追的上呢？

我们假设环的长度为C，那么此时再次追击两个指针的距离就为：C - 1,令T = C - 1,则：

T - 2 T - 4 T - 6 T - 8 ..... 最终有两种情况： :). T = 1，然后再减2 ==->== -1 ;). T = 2，然后再减2 ==->== 0

因此，这里又有两种情况，有了前面的推导，这里不难得出，当C为偶数时，则C - 1（T）为奇数，此时继续追不上，并且下一次也是一样，所以这里会陷入死循环；当C为奇数时，则C - 1为偶数，此时是追的上的。因此，当C为偶数时，永远追不上，当C为奇数时，追的上。

所以，通过以上分析，快指针每次走三步，慢指针每次走一步不一定能判断是否为带环链表，可能会陷入死循环，尽管陷入死循环就说明带环。

那么快指针每次走4步，走5步，走n步呢？这里就不是我们该探讨的范围了，相信大家心里已经有答案了。

环形链表 II

题目链接：==->== 传送门 ==<-==。
题目描述：给定一个链表的头节点 head ，返回链表开始入环的第一个节点。如果链表无环，则返回 null。注意：不允许修改链表。
与上一题不同的是，这一题首先是要判断链表是否带环，然后在带环的基础上返回链表入环的第一个节点。类似于下图：

在这里插入图片描述

解题思路：

这里直接说做法：先以第一题的思路使用快慢指针找到快指针和慢指针相遇的那个点，然后一个指针从该点开始走，一个指针从头开始走，每次走一步，最终两个指针会在入环的第一个节点相遇，然后返回这个节点。

解题代码：

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode *slow = head, *fast = head;

    while (fast && fast->next)
    {
    	// 快指针每次走两步
        fast = fast->next->next;
        // 慢指针每次走一步
        slow = slow->next;

		// 如果找到相遇的那个点，就开始找入环的第一个节点
        if (slow == fast)
        {
            struct ListNode *cur = slow;
            // 一个从头开始走，一个从当前节点开始走
            while (cur != head)
            {
                head = head->next;
                cur = cur->next;
            }
            // 最终相遇的那个点就是入环的第一个节点
            return cur;
        }
    }
	
	// 如果链表不带环，就返回NULL
    return NULL;
}

证明：为什么一个指针从快慢指针相遇的那个点开始走，一个指针从头开始走，最终两个指针会在入环的第一个节点处相遇？