引言
Kalman Filter,很多人刚听到这个名词时,总是会下意识认为这就是个滤波器。我这里想要重点声明的是,Kalman Filter不是滤波,它是一种信息融合的过程。
那么Kalman Filter到底是什么?它在那些方面有着应用,它的基本原理又是什么。如果你参考国内的论坛或者教材上,你一定会发现,大部分都是一些复杂公式与枯燥抽象的说明。这里我们将通过尽量通俗易懂的讲解来给大家解释下什么叫Kalman Fiter。
先睹为快
正如我前面提到的,从定义及复杂公式去理解卡尔曼滤波,对咱们凡人来说基本是不可能的。我们将公式简化,先从下面的公式来开始讲解:
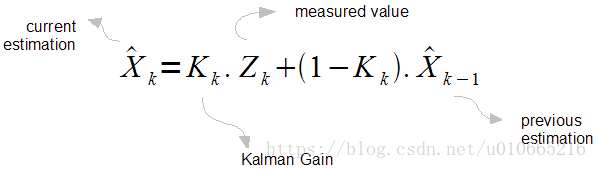
其中下标是指状态,这里我们可以把它看成间隔,比如
指1ms,
指2ms。我们的目的就是要找到在状态
时
的估计。在公式中
就是真实测量值。我们要牢记,这些测量值并不可靠。(如果这些测量值是可靠的,那么我们就没必要学kalman filter了:))。
指卡尔曼增益(这是整个公式中的核心点)。
就是上一状态时的估计。
在上述公式中,我们唯一未知的量就是卡尔曼增益。像测量值及上一状态估计,我们都已经知道了。当然了,求出卡尔曼增益并不简单,但是我们有方法来解决它。
我们从另一角度来思考,让我们假设卡尔曼增益为0.5,我们会得到什么呢?它就是个简单的平均!换句话说,我们应该找到对应于每个状态的更加智能化的卡尔曼增益系数。归根结底就是:
卡尔曼滤波器为每个结果状态找到最优的平均因子。 不知怎的,还记得一些关于过去的状态。
如何,Kalman Filter神奇吧!
分步指南
下面是分布指南,可以快速开始卡尔曼滤波。
Step1 构建模型
这是最重要的步骤。首先,你必须确保卡尔曼滤波的条件符合你的问题。
我们还记得卡尔曼滤波的两个典型方程(wiki):
第一个公式意味着每个可以通过一个线性随机方程来表示。任何一个
都是它前一状态的的只加上控制信号
及处理噪声
的线性组合。大多数的情况下,并不需要控制信号
。
第二个公式告诉我们,任何测量值(这里我们并不确定它是否准确)是当前状态信号值及测量噪声的线性组合,我们默认该值服从高斯分布。
这两个公式中的处理噪声及测量噪声,我们都认为是统计独立的。
方程式中的系数及
是一般形式的矩阵。但是在大多数的信号处理问题中,我们使用的模型中,这些系数都仅仅是数值。而且当这些值在状态间发生变化时,大多数的情况下,我们可以假设它们就是常数。
如果我们确定我们的系统符合这个模型(大多数的系统都是符合的),那么接下来,就只剩下估计噪声函数及
的均值和标准差。我们知道在现实生活中,没有哪个信号是纯高斯分布的,但是我们可以通过近似来进行假设。
这不是一个大问题,因为我们将看到卡尔曼滤波算法试图收敛到正确的估计,即使高斯噪声参数估计很差。
这里我们要始终牢记于心的是:“你估计噪声参数越准确,你就能获得更好的估计”
Step2 开始处理
如果你成功的将你的模型拟合到卡尔曼滤波器中,那么接下来的步骤就是决定必要的参数及你的初始值。
我们有两个不同的方程集合:时间更新(预测)及测量更新(校准)。两个方程集合都是应用在第个状态

我们在步骤一中建立模型,因此我们知道矩阵A,B和H。很可能,他们都是数值常量。并且他们极可能都是数值1.
我建议你们重新写下这些公式,并看看如何去简化这些公式。
.
上述公式中最痛苦的事儿就是确定R和Q了。R还相对比较容易找出,因为,通常来讲,我们对环境中的噪声还是比较确定的。但是寻找Q就并不明显了。在这个阶段,我们并不能给你一个指定的方法。
为了开始这个处理,我么需要知道和
的估计
Step3 迭代
在我们收集了我们需要的所有信息后,我们开始处理流程,现在我们可迭代估计。我们要牢记上一状态的估计将成为当前状态的估计的输入。

这里,先验估计指测量更新校准前的粗略估计。这里我们使用在测量更新公式中的先验值
在测量更新公式中,我们找到了在状态k时x的估计。并且找到了为了状态k+1估计所需要的值。
我们计算的卡尔曼增益,在下一个迭代步骤中并不需要。 这是一组方程中隐藏的,神秘的,最重要的部分。
我们在测量更新阶段评估的值也称为后验值。这也是说得通的。
一个简单的例子
如果小伙伴们在看到这里还有点稀里糊涂的,那么接下来我们找个例子来加深下理解。
现在,让我们努力去估计一个标量随机常数,例如来自某个信号源的“电压读数”。假设它有一个恒定的a V电压,但是我们读数会不准确,可能会读高了,也有可能读低了。我们假设测量噪声的的标准差为0.1 V。
现在我们来构建我们的模型:

就像我之前说的,我们可以把方程简化成非常简单的形式。
- 首先,我们有一个一维的信号的问题,因此我们模型中的每个系数都是数值,而不是矩阵。
- 我们并没有控制信号
- 因为信号是一个常数,那么常数A就是1,因为我们已经知道下一个值等于先前的值。我们很幸运,在这个例子中我们有一个恒定的值,但是即使它具有其他任何线性性质,我们都可以将它假设成1.
- 值H=1,因为我们知道测量值是由状态值和一些噪声组成的。你很少会遇到现实生活中,H与1不相同的情况
最后,我们假设我们得到了下面的测量值
TIME | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
VALUE | 0.39 | 0.50 | 0.48 | 0.29 | 0.25 | 0.32 | 0.34 | 0.48 | 0.41 | 0.45 |
我们应该从某处开始,比如说k=0。我们应该找到或者假设某个初始状态。这里我们给出了一些初始值。我们假设$X_0=0$并且$P_0=1$,那么为什么我们不选择$P_0=0$呢?这很简单。如果我们这样选择,那么就意味着环境中不存在噪声,而这个假设将导致在k状态下X的所有结果估计值为0(保留初始状态),所以我们一般不取$P_0=0$ 我们来写时间更新和测量更新方程
每一轮计算的步骤:
























