机械臂机器人——（4）Robotics Toolbox机器人仿真

文章目录

• ​​RoboticsToolbox基础用法​​

• ​​（1）二维空间位姿描述​​

• ​​二维空间位姿变换示例​​

• ​​（2）三维空间位姿描述​​

• ​​正交旋转矩阵​​
• ​​三维空间位姿变换示例​​

• ​​2.三角度表示法​​

• ​​（1）欧拉角​​

• ​​示例：欧拉角与旋转矩阵的相互转化​​

• ​​（2）RPY角​​

• ​​示例：RPY角与旋转矩阵的相互转化​​

• ​​（3）双向量角表示法​​

• ​​示例：双向量转化为旋转矩阵​​

• ​​（4）向量和旋转角表示法​​

• ​​示例：向量旋转角与旋转矩阵的相互转化​​

• ​​（5）单位四元数表示法​​

• ​​示例：四元数用法​​

• ​​3.RoboticsToolbox建立机器人模型​​

• ​​（1）建立机器人模型函数​​

• ​​Link类函数​​
• ​​Seriallink类函数​​

• ​​（2）DH参数​​

• ​​标准DH参数​​
• ​​改进DH参数​​

• ​​（3）改进DH参数，建立机器人模型步骤​​

• ​​示例​​

• ​​（4）标准DH参数建模​​
• ​​（5）标准DH和改进DH的区别​​

• ​​4.正逆运动学、轨迹规划​​

• ​​（1）正运动学​​

• ​​puma560机械臂正运动学示例​​

• ​​（2）逆运动学​​

• ​​puma560机械臂逆运动学示例​​

• ​​（3）轨迹规划​​

• ​​示例：sawyer机器人轨迹规划​​

• ​​5.速度和静力​​

• ​​（1）雅可比矩阵​​
• ​​（2）分解速度运动控制​​

RoboticsToolbox基础用法

（1）二维空间位姿描述

二维空间位姿变换示例

T1 = SE2(1,3,30,"deg");
trplot2(T1,"frame","1","color","b");
axis([0 5 0 5]);
T2=trans12(3, 4);
hold on;
trplot2(T2,"frame","2","color","r");

运行效果：

（2）三维空间位姿描述

正交旋转矩阵

三维空间位姿变换示例

R1=rotx(30,"deg")*roty(50,"deg"); %绕x轴旋转30°，再绕y轴旋转50°
trplot(R1,"frame","A", "color", "b"); %画出旋转矩阵R1
tranimate(R1,"frame","A", "color", "b"); %将R1的变换做成动画
R2=roty(50,"deg")*rotx(30,"deg"); %绕y轴旋转50°，再绕x轴旋转30°
hold on
trplot(R2,"frame","B", "color", "r"); %画出旋转矩阵R2
tranimate(R2,"frame","B", "color", "r"); %将R2的变换做成动画

运行效果：

R1和R2是两个完全不同的旋转矩阵，说明R1和R2具有不可交性。

2.三角度表示法

（1）欧拉角

欧拉角是在

示例：欧拉角与旋转矩阵的相互转化

R3=rotz(0.1)*roty(0.2)*rotz(0.3); % 构造旋转矩阵R3
R4=eul2r(0.1,0.2,0.3); % 欧拉角转化为旋转矩阵
eul=tr2eul(R3); % 旋转矩阵转化为欧拉角

（2）RPY角

RPY角是在固定坐标系A下，以固定的XYZ轴作为旋转的基准。三个角分别为Row（回转），Pitch（俯仰）和Yaw（偏转），可以用右手坐标系表示，食指为Row，中指为Pitch，大拇指为Yaw。

示例：RPY角与旋转矩阵的相互转化

R5=rotz(0.3)*roty(0.2)*rotx(0.1); % 构造旋转矩阵R5
R6=rpy2r(0.3,0.2,0.1); % rpy角转化为旋转矩阵
eul=tr2rpy(R5); % 旋转矩阵转化为rpy角

（3）双向量角表示法

示例：双向量转化为旋转矩阵

a=[1 0 0]';
o=[0 1 0]';
R7=oa2r(o,a); % 将双向量o,a转化为旋转矩阵R7

（4）向量和旋转角表示法

示例：向量旋转角与旋转矩阵的相互转化

（5）单位四元数表示法

示例：四元数用法

s=0.98335;
v=[0.034271, 0.10602, 0.14357];
Q=UnitQuaternion(s,v); % 组成四元数
q=Q.inv(); % 求共轭
Q.display(); % 打印出四元数
Q.plot(); % 画出出四元数
Q.animate(); % 动画展示四元数
TT=Q.T; % 制作齐次变换矩阵
RR=Q.R; % 制作旋转矩阵
rpy=Q.torpy(); % 转换成rpy角
eul=Q.toeul(); % 转换成eul角

3.RoboticsToolbox建立机器人模型

（1）建立机器人模型函数

Link类函数

Seriallink类函数

（2）DH参数

标准DH参数

改进DH参数

（3）改进DH参数，建立机器人模型步骤

示例

clc;
clear;
% 定义各个连杆以及关节类型，默认为转动关节
%           theta      d        a        alpha
%               连杆偏距参数d 连杆长度参数 关节偏角参数alpha
L1=Link([     0        0        0          0], 'modified'); % [四个DH参数], options
L2=Link([    -pi/2   0.1925,   0.081     -pi/2], 'modified');
L3=Link([     0       0.4       0        -pi/2], 'modified');
L4=Link([     0      0.1685,    0        -pi/2], 'modified');
L5=Link([     0      0.4,       0         pi/2], 'modified');
L6=Link([     0      0.1363     0         pi/2], 'modified');
L7=Link([     0      0.13375    0        -pi/2], 'modified');
% 
b=isrevolute(L1);
robot=SerialLink([L1,L2,L3,L4,L5,L6,L7]); % 将七个连杆组成机械臂
robot.name='modified sawyer';
robot.display(); % 展示出
view(3); % 解决robot.teach()和plot的索引超出报错
robot.teach();
robot.plot([0 -pi/2 0 0 0 0 0]);

（4）标准DH参数建模

clc;
clear;
% 定义各个连杆以及关节类型，默认为转动关节
%           theta      d        a        alpha
%               连杆偏距参数d 连杆长度参数 关节偏角参数alpha
L1=Link([     0        0        0          0], 'standard'); % [四个DH参数], options
L2=Link([    -pi/2   0.1925,   0.081     -pi/2], 'standard');
L3=Link([     0       0.4       0        -pi/2], 'standard');
L4=Link([     0      0.1685,    0        -pi/2], 'standard');
L5=Link([     0      0.4,       0         pi/2], 'standard');
L6=Link([     0      0.1363     0         pi/2], 'standard');
L7=Link([     0      0.13375    0        -pi/2], 'standard');
% 
b=isrevolute(L1);
robot=SerialLink([L1,L2,L3,L4,L5,L6,L7]); % 将七个连杆组成机械臂
robot.name='standard sawyer';
robot.display(); % 展示出
view(3); % 解决robot.teach()和plot的索引超出报错
robot.teach();
robot.plot([0 -pi/2 0 0 0 0 0]);

（5）标准DH和改进DH的区别

4.正逆运动学、轨迹规划

（1）正运动学

puma560机械臂正运动学示例

mdl_puma560; % 加载puma560模型
qz    % 零角度
qr    % 就绪状态，机械臂甚至且垂直
qs    % 伸展状态，机械臂伸直且水平
qn    % 标准状态，机械臂处于灵巧工作状态
view(3);
p560.plot(qn);
T=p560.fkine(qn);

（2）逆运动学

puma560机械臂逆运动学示例

（3）轨迹规划

示例：sawyer机器人轨迹规划

clc;
clear;
% 定义各个连杆以及关节类型，默认为转动关节
%           theta      d        a        alpha
%               连杆偏距参数d 连杆长度参数 关节偏角参数alpha
L1=Link([     0        0        0          0], 'modified'); % [四个DH参数], options
L2=Link([    -pi/2   0.1925,   0.081     -pi/2], 'modified');
L3=Link([     0       0.4       0        -pi/2], 'modified');
L4=Link([     0      0.1685,    0        -pi/2], 'modified');
L5=Link([     0      0.4,       0         pi/2], 'modified');
L6=Link([     0      0.1363     0         pi/2], 'modified');
L7=Link([     0      0.13375    0        -pi/2], 'modified');
% 
b=isrevolute(L1);
robot=SerialLink([L1,L2,L3,L4,L5,L6,L7],'name','FANUC'); % 将七个连杆组成机械臂
robot.name='modified sawyer';
robot.display(); % 展示出

init_ang=[0 0 0 0 0 0 0];
targ_ang=[pi/4,-pi/3,pi/5,pi/2,-pi/4,pi/2,pi/3];
step=200;
[q,qd,qdd]=jtraj(init_ang,targ_ang,step); %关节空间规划轨迹，得到机器人末端运动的[位置，速度，加速度]
T0=robot.fkine(init_ang); % 正运动学解算
Tf=robot.fkine(targ_ang);
subplot(2,4,3); i=1:7; plot(q(:,i)); title("位置"); grid on;
subplot(2,4,4); i=1:7; plot(qd(:,i)); title("速度"); grid on;
subplot(2,4,7); i=1:7; plot(qdd(:,i)); title("加速度"); grid on;

Tc=ctraj(T0,Tf,step);
Tjtraj=transl(Tc);
subplot(2,4,8); plot2(Tjtraj, 'r');
title('p1到p2直线轨迹'); grid on;
subplot(2,4,[1,2,5,6]);
plot3(Tjtraj(:,1),Tjtraj(:,2),Tjtraj(:,3),"b"); grid on;
hold on;
view(3); % 解决robot.teach()和plot的索引超出报错
qq=robot.ikine(Tc);
robot.plot(qq);

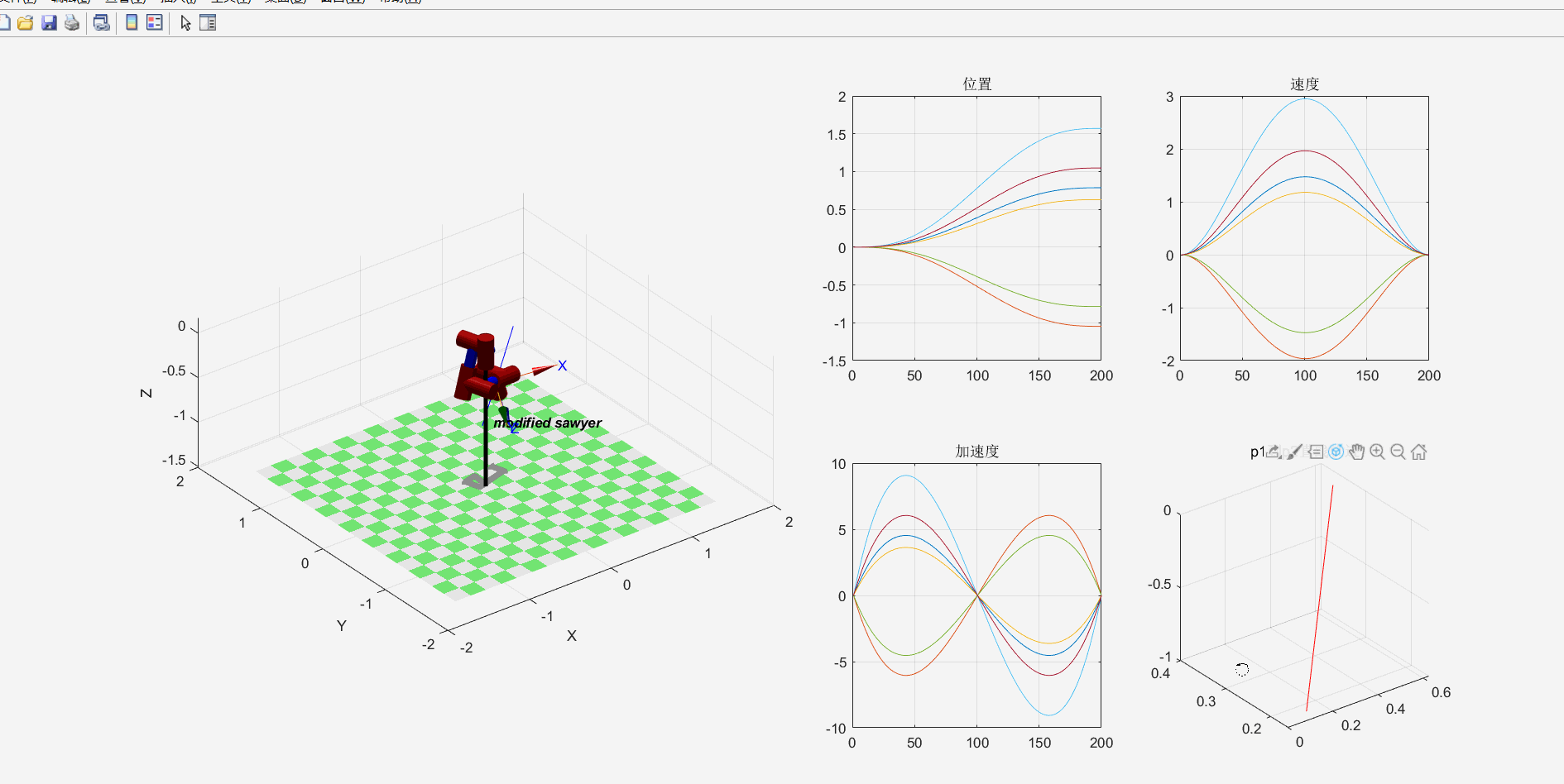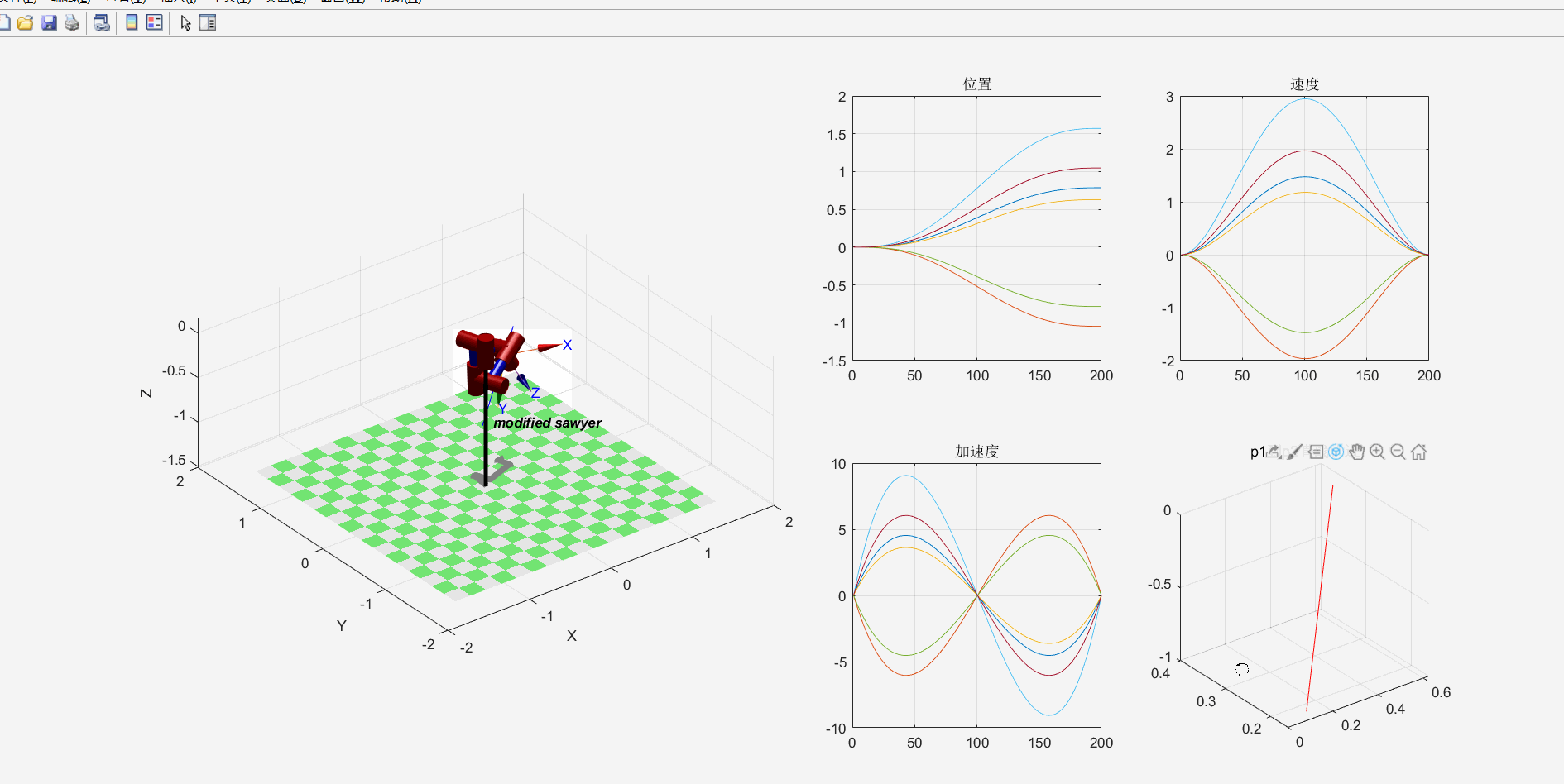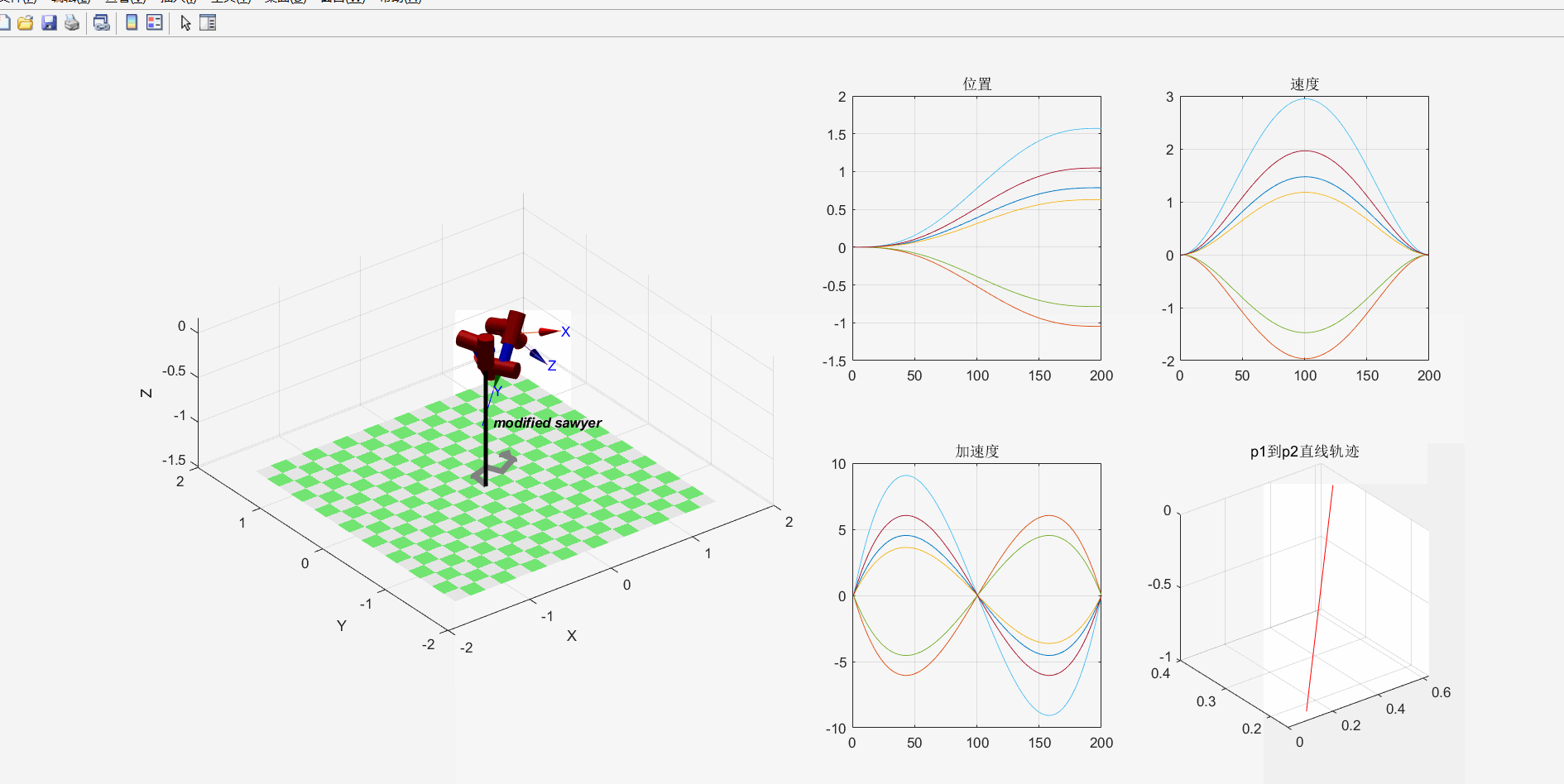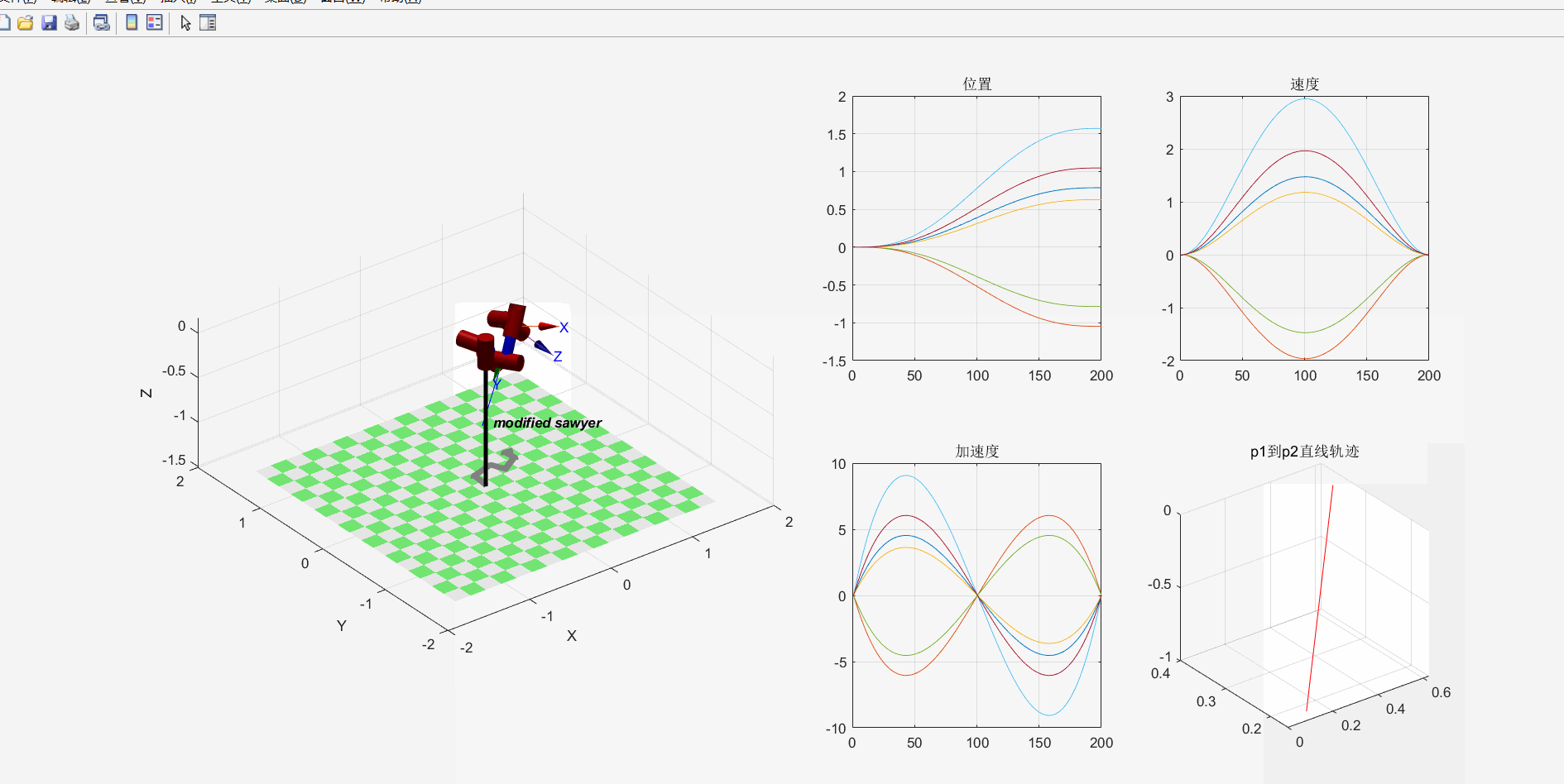
5.速度和静力

（1）雅可比矩阵

（2）分解速度运动控制