LeetCode_Array_Pascal‘s Triangle杨辉三角I/II（C++）【动态规划】

目录

​​1，题目描述​​

​​杨辉三角I​​

​​杨辉三角II​​

​​2，解题思路​​

​​3，AC代码​​

​​杨辉三角I​​

​​杨辉三角II​​

​​4，解题过程​​

​​杨辉三角I​​

​​杨辉三角II​​

---

1，题目描述

杨辉三角I

给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。

在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

输入: 5
输出:
[
     [1],
    [1,1],
   [1,2,1],
  [1,3,3,1],
 [1,4,6,4,1]
]

 

杨辉三角II

给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。

在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

输入: 3
输出: [1,3,3,1]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/pascals-triangle-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2，解题思路

这两个题目思路基本相同，放在一起介绍了；

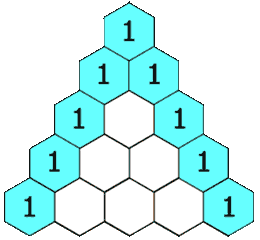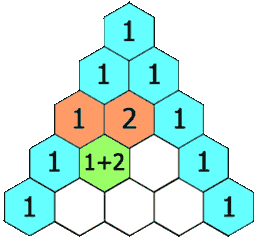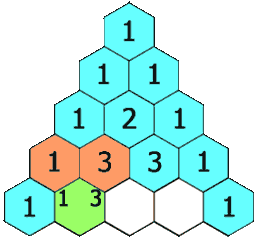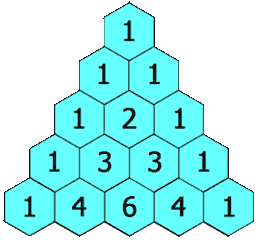
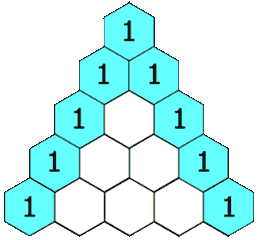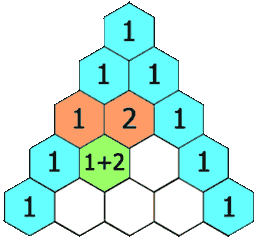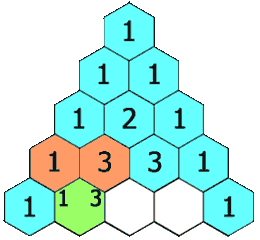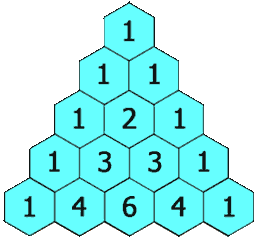
如图，杨辉三角的特点：两边元素为一，中间元素为其左右两肩元素之和；

状态转移方程：tem[j] = tem[j] + tem[j - 1]。

可以看出仅借助于一个数组时，计算新的 tem[j] 需要用到旧的 tem[j] 和 tem[j - 1]，因而需要从右向左遍历；

比如当前得到的最新数组tem = [1，2，1]；

• 首先在tem数组末尾加个1，tem.push_back(1)，此时tem = [1，2，1，1]，使得数组的大小与下一行匹配；
• 从右向左tem数组的迭代过程如下：

[1，2，1]        =》[1，2，1，1]；

[1，2，1，1]  =》 [1，2，3，1]；

[1，2，3，1]  =》 [1，3，3，1]；

具体代码实现如下：

tem.push_back(1); for(int j = tem.size() - 2; j > 0; --j){ tem[j] += tem[j - 1]; }

 

3，AC代码

杨辉三角I

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> ans;
        if(numRows < 1) return ans;     // 前0行即空
        vector<int> tem;
        for(int i = 0; i < numRows; ++i){
            tem.push_back(1);
            for(int j =  tem.size() - 2; j > 0; --j){
                tem[j] += tem[j - 1];
            }
            ans.push_back(tem);
        }
        return ans;
    }
};

杨辉三角II

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> ans;
        ans.push_back({1});                             // 这里的0表示第一行
        for(int i = 0; i < rowIndex; ++i){
            ans.push_back(1);
            for(int j = ans.size() - 2; j >= 1; --j){   // 从右向左遍历
                ans[j] += ans[j - 1];                   // 状态转移方程 覆盖掉原先的值来节省空间
            }
        }
        return ans;
    }
};

 

4，解题过程

简单题目，规律也很直观，一发入魂o(*￣▽￣*)ブ

杨辉三角I

杨辉三角II