2019HDU多校赛 第五场 A HDU 6624 fraction（辗转相除法）

 

 

大致题意：给你一个分数在p下的逆元表示形式，现在让你反推这个分数的a/b的形式，求最小的b且0<a<b。

首先，我们推一下式子：

                                       

                                             

                       

                                                                

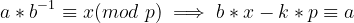
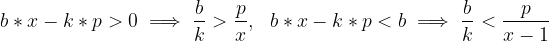
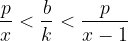
然后本题p和x都知道，所以我们本质上要求的就是一个满足条件的b而且b最小。然后这个问题就变成一个很经(bu)典(hui)的问题，做法就是辗转相除法。步骤如下(假设两边的限制是a/b和c/d，中间的数字为x/y)：

1、看两个数字之间是否有整数，如果有，那么取x为之间最小的整数，y为1，同时x把之前减去的

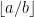
加回去，回代答案结束算法。2、化简为真分数，两端限制同时减去

。

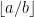
3、分子分母和区间取反，回到步骤1。 

那么，这样子类似与辗转相除法的过程得到的b为什么一定是最小的呢？可以这么理解，因为到最后一步，我的取法是让分子和分母都取最小的，而之前的变换相当于只是一个恒等变换，所以这个最小可以从最后一步传到一开始，因此这个是最小的。然后复杂度的话，相当于对一开始的p和x做一个辗转相除法，因为减去

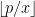
就相当于取模，交换分子分母相当于交换除数和被除数，因此复杂度就是辗转相除的复杂度，为O(logN)。具体见代码：

#include<bits/stdc++.h>
#define N 100010
#define INF 0x3f3f3f3f
#define eps 1e-5
#define pi 3.141592653589793
#define mod 998244353
#define P 1000000007
#define LL long long
#define pb push_back
#define fi first
#define se second
#define cl clear
#define si size
#define lb lower_bound
#define ub upper_bound
#define bug(x) cerr<<#x<<"      :   "<<x<<endl
#define mem(x) memset(x,0,sizeof x)
#define sc(x) scanf("%d",&x)
#define scc(x,y) scanf("%lld%lld",&x,&y)
#define sccc(x,y,z) scanf("%d%d%d",&x,&y,&z)
using namespace std;

void Euclid(LL a,LL b,LL c,LL d,LL &x,LL &y)
{
    LL z=a/b+1;
    if (z<c/d+(c%d>0))
    {
        x=z,y=1;
        return;
    }
    z--;
    a-=z*b; c-=z*d;
    Euclid(d,c,b,a,y,x);
    x+=z*y;
}

int main(){
    int T;
    sc(T);
    while(T--){
        LL c,p,x=0,y=0;
        scc(p,c);
        Euclid(p,c,p,c-1,x,y);
        LL a=c*x-p*y;
        printf("%lld/%lld\n",a,x);
    }
}