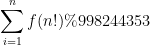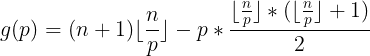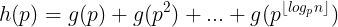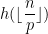计蒜客 2019ICPC 徐州网络赛 H function（Min25筛）

 

 

大致题意：定义f(n)表示n分解质因数后，各个质因子的幂次之和，现在让你计算

。

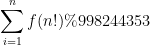
显然只需要考虑质数，计算质数的贡献。我们令

                                         

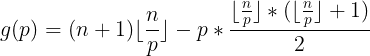
那么质数p的贡献就是：

                                            

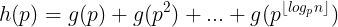
对于小于

的质数，我们可以直接暴力求解。对于大于

，显然有h(p)=g(p)。对于这部分显然不能直接暴力做，我们观察到函数h(p)=g(p)在这种情况下可以写成

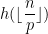
和

。然后你会发现，这个东西是可以数论分块的。我们把

用减号分为前后两个部分，前面部分相当于是(n+1)乘以某段区间内的质数个数，而后半部分相当于是

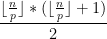
乘以某段区间内的质数的和。那么问题转换为了求质数个数和质数和的前缀和。

接下来就是常规做法了，用Min25搞搞就行了。具体见代码：

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f3f3f3f3fll
#define eps 1e-6
#define LL long long
#define pb push_back
#define fi first
#define se second
#define cl clear
#define si size
#define lb lower_bound
#define ub upper_bound
#define bug(x) cerr<<#x<<"      :   "<<x<<endl
#define mem(x) memset(x,0,sizeof x)
#define sc(x) scanf("%lld",&x)
#define scc(x,y) scanf("%d%d",&x,&y)
#define sccc(x,y,z) scanf("%d%d%d",&x,&y,&z)
using namespace std;

const int N = 2e5 + 10;
const LL mod = 998244353;
const LL inv = (1 + mod) / 2;

LL n,sz,p[N],w[N],g[N],h[N],id[N],ps[N];
bool isp[N];

inline void init(int N)
{
    sz=0;
    for(int i=2;i<=N;i++)
    {
        if(!isp[i])p[++sz]=i,ps[sz]=(ps[sz-1]+i)%mod;
         for(int j=1;j<=sz&&i*p[j]<=N;j++)
         {
            isp[i*p[j]]=1;
            if(i%p[j]==0) break;
        }
    }
}

int main()
{
    sc(n);
    LL block=sqrt(n);
    init(block);
    LL ans=0;
    for(int i=1;i<=sz;i++)
    {
        if (p[i]>n) break;
        for(LL x=p[i];x<=n;x*=p[i])
        {
            LL tmp=n/x%mod;
            ans+=((n+1)%mod*tmp%mod-(1+tmp)%mod*tmp%mod*inv%mod*x%mod+mod)%mod;
        }
        ans=(ans%mod+mod)%mod;
    }
    int M=0;
    for(LL i=1,last;i<=n;i=last+1)
    {
        LL len=n/i; last=n/len;
        w[++M]=len; g[M]=(w[M]-1)%mod;
        h[M]=w[M]%mod*((w[M]+1)%mod)%mod;
        h[M]=(h[M]*inv%mod-1+mod)%mod;
        if(len<=block) id[len]=M;
    }
    for(int i=1;i<=sz;i++)
        for(int j=1;j<=M&&p[i]*p[i]<=w[j];j++)
        {
            int op=w[j]/p[i]<=block?id[w[j]/p[i]]:n/(w[j]/p[i]);
            (g[j]-=g[op]-i+1)%=mod; (h[j]-=p[i]*(h[op]-ps[i-1])%mod)%=mod;
            if (h[j]<0) h[j]+=mod; if (g[j]<0) g[j]+=mod;
        }
    for(LL i=1;i<block;i++)
    {
        (ans+=(n+1)%mod*i%mod*(g[i]-g[i+1]+mod)%mod)%=mod;
        (ans-=i%mod*(i+1)%mod*inv%mod*(h[i]-h[i+1]+mod)%mod)%=mod;
        (ans+=mod)%=mod;
    }
    printf("%lld\n",ans);
}