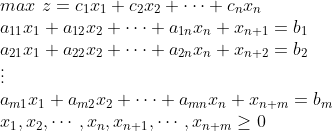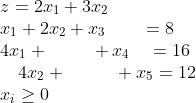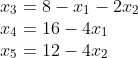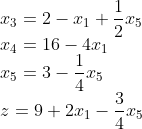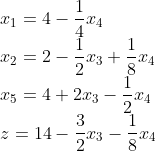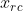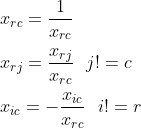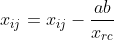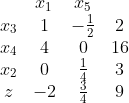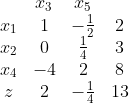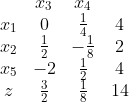线性函数:按比例,一阶导数为常数的函数。
松弛变量:引入新的变量,且保持变量间的关系不变。
提到线性规划,自己最先想起的是高中的各种数学题。
线性规划问题的标准形式:

用松弛变量技术把不等式化成等式:
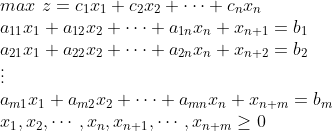
单纯性算法的思想:
从一个基本可行解出发,寻找能使得目标函数更优的另一个解,迭代下去直到找不到。使用这种方法避免大量的无用比较。
例子:
从
FOREVER284LOVE的
《
线性规划与单纯形法》
http://wenku.baidu.com/link?url=05wVz6KCN_d2m-ecjJ2TsRgdD0IttSF0jQ0BI8W-luZRxPARLE5XNRlSyIXBYwoI5lA711iVUkW14xfO3O4UWXAewW3PLkg1puZdiYcvl9u
看到的一题,以它为例:
某工厂在计划期内要安排生产I、 II两种产品, 已知生产单位产品所需的设备台时及A、B两种原材 料的损耗,如表所示:

该工厂每生产一件产品Ⅰ可获利2元,每生产一件产品Ⅱ可获利3元,问应如何安排计划使该工厂获利最多?
解:列出标准形式:
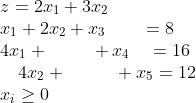
所以:
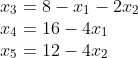
称Z表达式中的变量为非基变量(x1,x2),约束方程中剩余的变量是基变量 (x3,x4,x5)
当非基变量全是0时,Z有一个X解。这一个解作为初始解。想要让Z变大,那么正整数系数的变量一定要变大。
可以选一个最大系数的变量x2,那么x1随着x2变大将变成0,那么从约束方程可以看出,X5先变成0,故把X1和X5作为新的非基变量。
有:
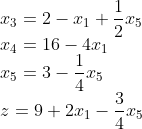
存在正系数说明目标函数还能变大。令x5=0,从约束方程可以看出,x1最大取2,此时x3=0。那么新的非基变量就是x3, x5.于是得到:
重复刚刚的步骤,得到:
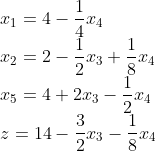
当x3=x4=0时得到最优解z=14
把刚刚的过程表格化:(表格化思想来自《组合数学及应用》)


我们发现,事实上,一个基本变量和一个非基本变量互换后得到了下一个方程组。
寻找互换的非基本变量:对应的Z行系数是负数的,选择它,有多个负数就选择最小的那个。对应的非基本变量就是选择项。
寻找互换的基本变量:非基本变量增大,基本变量减小,谁先变成0,谁就是基本变量。数值元素变化规律:称参与互换的非基变量所在列是主元列,基本变量所在行是主元行。
设当前的主元行是r,主元列是c,主元为
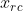
, 各个位置的元素值是

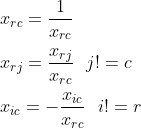
设投影列元素a,投影行元素b。投影是相对主元行和主元列而言,上图中16的投影行元素是12,投影列元素是0
那么其他的元素就是:
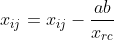
后续变化:
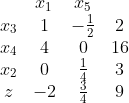
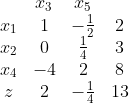
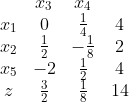
嗯嗯,就是这个流程。
设n个变量,m个约束条件。
那么修改数字矩阵的部分写成程序就是
a[r][c] = 1 / a[r][c];
for(int j = 0; j <= n; j++) if(j != c) a[r][j] *= a[r][c];
for(int i = 0; i <= m; i++)
if(i != r) {
for(int j = 0; j <= n; j++)
if(j != c) a[i][j] -= a[i][c] * a[r][j];
a[i][c] = -a[i][c] * a[r][c];
}
寻找基本变量和非基本变量,判断有界、无解、无界部分是真不会写了,参考别人的模板。
献上一题:
10498 - Happiness
https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1439
大意:买N件物品,每个人对每件物品有自己的满意度,且有一个满意度和的限制。每一件物品有自己的价格,问能花费的最多的钱。
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const int maxm = 500; // 约束数目上限
const int maxn = 500; // 变量数目上限
const double INF = 1e100;
const double eps = 1e-10;
struct Simplex {
int n; // 变量个数
int m; // 约束个数
double a[maxm][maxn]; // 输入矩阵
int B[maxm], N[maxn]; // 算法辅助变量
void calc(int r, int c) {
swap(N[c], B[r]);
a[r][c] = 1 / a[r][c];
for(int j = 0; j <= n; j++) if(j != c) a[r][j] *= a[r][c];
for(int i = 0; i <= m; i++)
if(i != r) {
for(int j = 0; j <= n; j++)
if(j != c) a[i][j] -= a[i][c] * a[r][j];
a[i][c] = -a[i][c] * a[r][c];
}
}
bool check() {
while(1) {
int r, c;
double p = INF;
for(int i = 0; i < m; i++){
if(a[i][n] < p) {
r=i;
p = a[r][n]; // 最右边的常数列
}
}
if(p > -eps) return true; // 都是正数的话可行。
p = 0;
for(int i = 0; i < n; i++) {
if(a[r][i] < p){
c=i;
p = a[r][c]; // 找最小列
}
}
if(p > -eps) return false; // r对应的所有列都是正数,没有负数,无解。
p = a[r][n]/a[r][c];
for(int i = r+1; i < m; i++)
if(a[i][c] > eps) {
double v = a[i][n] / a[i][c];
if(v < p) {
r = i;
p = v;
}
}
calc(r, c);
}
}
// 解有界返回1,无解返回0,无界返回-1。b[i]为x[i]的值,ret为目标函数的值
int simplex(int n, int m, double x[maxn], double& ret) {
this->n = n;
this->m = m;
for(int i = 0; i < n; i++) N[i] = i;
for(int i = 0; i < m; i++) B[i] = n+i;
if(!check()) return 0;
while(1){
int r, c;
double p = 0;
for(int i = 0; i < n; i++) if(a[m][i] > p) {
c = i;
p = a[m][c];
}
if(p < eps) {
for(int i = 0; i < n; i++) if(N[i] < n) x[N[i]] = 0;
for(int i = 0; i < m; i++) if(B[i] < n) x[B[i]] = a[i][n];
ret = -a[m][n];
return 1;
}
p = INF;
for(int i = 0; i < m; i++) if(a[i][c] > eps) {
double v = a[i][n] / a[i][c];
if(v < p) { r = i; p = v; }
}
if(p == INF) return -1;
calc(r, c);
}
}
};
Simplex solver;
int main()
{
//freopen("cin.txt","r",stdin);
int n, m;
while(~scanf("%d%d", &n, &m)) {
for(int i = 0; i < n; i++) scanf("%lf", &solver.a[m][i]); // 目标函数
solver.a[m][n] = 0;
for(int i = 0; i < m; i++)
for(int j = 0; j < n+1; j++)
scanf("%lf", &solver.a[i][j]);
double ans,x[maxn];
solver.simplex(n,m,x,ans);
ans *= m;
//printf("Nasa can spend %d taka.\n", int(ans+0.5)); // 至少花费的:3.008-->4
printf("Nasa can spend %d taka.\n", (int)floor(ans + 1 - eps));
}
return 0;
}