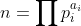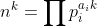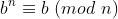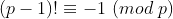三个特殊的同余式

介绍三个特殊而重要的同余式：

欧拉定理（Euler theorem）

费马小定理（Fermat's little theorem）

威尔逊定理（Wilson theorem）

1.欧拉定理：如果a、p是正整数，且互质，那么有

证明：设和P互质且小于P的正整数集合是

进一步：

所以  

   在集合S内。

那么，

有：

2.而当P是素数的时候，欧拉定理就是费马小定理：

费马小定理除了能用于求解逆元之外，还有一个强大的功能：在满足条件下，降幂。

设正整数

那么：

一个例子：

POJ 1845 Sumdiv

​​http://poj.org/problem?id=1845​​

大意：求解A^B的因子和，输出模9901的结果。

分析：设N分解成：

,则

那么问题的结果就是：

于是这涉及到逆元，还可用费马小定理降幂。不过还有陷阱。。（此题原来也做过，曾经就因为不知道WA在哪里，改成了二分递归思路）

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long LL;
const LL N=5e5+10,mod=9901;
LL fac[N],cnt;
bool vis[N];
void getfac(){
    for(LL i=2;i<N;i++){
        if(!vis[i])  fac[cnt++]=i;
        for(LL j=0;j<cnt&&fac[j]*i<N;j++){
            vis[i*fac[j]]=1;
            if(i%fac[j]==0)  break;
        }
   }
}
LL sta[N],pow[N],top;
void solve(LL x){
    memset(pow,0,sizeof(pow));
    top=0;
    for(LL i=0;i<cnt&&fac[i]<=x;i++){  //i<cnt
        if(x%fac[i]==0){
            sta[top]=fac[i];
            while(x%fac[i]==0){
                x/=fac[i];
                pow[top]++;
            }
            top++;
        }
    }
    if(x>1){
        sta[top]=x;
        pow[top]++;
        top++;
    }
}
void ex_gcd(LL a,LL b,LL &d,LL &x,LL &y){
    if(b==0){
        d=a; x=1; y=0;
        return ;
    }
    ex_gcd(b,a%b,d,x,y);
    LL t=x;
    x=y;
    y=t-a/b*y;
}
LL power(LL a,LL p){
    a=a%mod;
    LL ans=1;
    p=p%(mod-1); // 费马小定理
    while(p){
        if(p&1)  ans=ans*a%mod;
        a=a*a%mod;
        p>>=1;
    }
    return ans;
}
int main()
{
    //freopen("cin.txt","r",stdin);
    getfac();
    LL A,B;
    while(cin>>A>>B){
        if(A==0){
            puts("0"); // 在这里 0^0=0
            continue;
        }
        if(B==0){
            puts("1");
            continue;
        }
        solve(A);
        LL ans=1;
        for(LL i=0;i<top;i++){
            LL temp=1;
            if(sta[i]%mod==0) continue;
            if(sta[i]%mod==1){ // "互质" != "(mod m)=1"
                temp=(pow[i]*B+1)%mod;
                ans=ans*temp%mod;
                continue;
            }
            LL d=1,ni=1,y=1;
            ex_gcd(sta[i]-1,mod,d,ni,y);
            ni=(ni%mod+mod)%mod;
            temp=power(sta[i],(pow[i]*B+1));
            temp=(temp-1+mod)%mod;
            ans=ans*temp%mod*ni%mod;
        }
        printf("%lld\n",ans);
    }
    return 0;
}

/*
ex_gcd(i,9901,d,x,y);  // i=0 -> x=0  i=-1 -> x=1
*/

费马小定理告诉我们，当n是一个素数时有：

符合这一特征，但是却是合数的是 伪素数(pseudoprime)。

3.wilson 定理

如果p是素数，那么

证明：如果p是一个素数，那么对于等式

，其中0<a<p，只有a=1 或者a=p-1时逆元和本身相等，其他数字的逆元是在1——p-1内的不同数字。

由此，

那么，

由此产生的推论：

如果正整数n>=2，且

，那么n是一个素数。