算法:堆(Heap)
Heap 可以用来实现优先级队列,也可以用来做堆排序,本文简单的做个介绍。
Heap规则
- 是一个完全二叉树,隐含的意思是:他是平衡的、使用数组进行存储也是连续的。
- 给定的任意节点,该节点小于等于其父亲节点,大于他们的孩子节点。
基础知识
对于一个完全二叉树,如果将其存储到数组中,给定父节点的索引为:x,则:
- left child's index is:2*x + 1。
- right child's index is:2*x + 2。
- root's index is:0.
说明:上面的公式很容易自己推到出来,有兴趣的朋友可以推到一下,这样就不用记住这个特性了。
图示

存储到数组的顺序为:先存储第一层,然后是第二层,直到第 N 层。
操作
添加和删除后还必须保证 Heap 满足规则。
添加
添加前


添加 6


先将 6 添加到完全树的下一个节点,然后沿着祖先路径,将其插入到合适的节点(不一定是根节点)。
代码
1 public void Insert(T item)
2 {
3 if (this.IsFull())
4 {
5 throw new InvalidOperationException("容量已满,不能插入!");
6 }
7
8 _items[_length++] = item;
9 this.MoveUp(_length - 1);
10 }
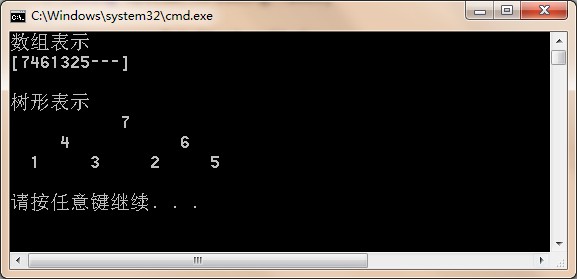
结果


删除最大值
接着上面的例子执行删除
先将删除根节点(6),再将完全树最后的节点(2)直接移动到根节点。


接着将 2 向下插入到合适的节点,比如:5 > 4 && 5 > 2,因此结果是:


代码
1 public T Remove()
2 {
3 if (this.IsEmpty())
4 {
5 throw new InvalidOperationException("容量已空,不能删除!");
6 }
7
8 var result = _items[0];
9 _items[0] = _items[--_length];
10
11 this.MoveDown(0);
12
13 return result;
14 }
完整代码
1 using System;
2 using System.Collections.Generic;
3 using System.Linq;
4 using System.Text;
5 using System.Threading.Tasks;
6
7 namespace DataStuctureStudy.Heaps
8 {
9 class HeapTest
10 {
11 public static void Test()
12 {
13 var heap = new Heap<int>(10);
14 heap.Insert(1);
15 heap.Insert(2);
16 heap.Insert(3);
17 heap.Insert(4);
18 heap.Insert(5);
19 heap.Insert(6);
20 heap.Display();
21 heap.Remove();
22 heap.Display();
23 }
24
25 class Heap<T>
26 where T : IComparable<T>
27 {
28 private T[] _items;
29 private int _length;
30
31 public Heap(int size)
32 {
33 _items = new T[size];
34 }
35
36 public void Display()
37 {
38 Console.WriteLine("数组表示");
39 Console.Write("[");
40 for (var i = 0; i < _items.Length; i++)
41 {
42 if (i < _length)
43 {
44 Console.Write(_items[i]);
45 }
46 else
47 {
48 Console.Write('-');
49 }
50 }
51 Console.WriteLine("]");
52 Console.WriteLine();
53
54 Console.WriteLine("树形表示");
55 var row = 0;
56 var column = 0;
57 var level = (int)Math.Ceiling(Math.Log(_length + 1, 2));
58 var width = (int)Math.Pow(2, level);
59 for (var i = 0; i < _length; i++)
60 {
61 this.Display(_items[i], width, row, column);
62
63 if ((i + 1) == Math.Pow(2, row + 1) - 1)
64 {
65 row++;
66 column = 0;
67 Console.WriteLine();
68 }
69 else
70 {
71 column++;
72 if (i == _length - 1)
73 {
74 Console.WriteLine();
75 }
76 }
77 }
78
79 Console.WriteLine();
80 }
81
82 private void Display(T item, int width, int row, int column)
83 {
84 var step = (int)((width * 3) / Math.Pow(2, row));
85 var itemLength = item.ToString().Length;
86 Console.Write(item.ToString().PadLeft((step + itemLength) / 2).PadRight(step));
87 }
88
89 public void Insert(T item)
90 {
91 if (this.IsFull())
92 {
93 throw new InvalidOperationException("容量已满,不能插入!");
94 }
95
96 _items[_length++] = item;
97 this.MoveUp(_length - 1);
98 }
99
100 private void MoveUp(int index)
101 {
102 var bottom = _items[index];
103 var current = index;
104
105 while (current > 0)
106 {
107 var parent = (current - 1) / 2;
108 if (_items[parent].CompareTo(bottom) > 0)
109 {
110 break;
111 }
112
113 _items[current] = _items[parent];
114 current = parent;
115 }
116
117 _items[current] = bottom;
118 }
119
120 public T Remove()
121 {
122 if (this.IsEmpty())
123 {
124 throw new InvalidOperationException("容量已空,不能删除!");
125 }
126
127 var result = _items[0];
128 _items[0] = _items[--_length];
129
130 this.MoveDown(0);
131
132 return result;
133 }
134
135 private void MoveDown(int index)
136 {
137 var top = _items[index];
138 var current = index;
139
140 while (current < _length)
141 {
142 var large = 0;
143 var left = 2 * current + 1;
144 var right = left + 1;
145
146 if (left < _length && right < _length)
147 {
148 if (_items[left].CompareTo(_items[right]) >= 0)
149 {
150 large = left;
151 }
152 else
153 {
154 large = right;
155 }
156 }
157 else if (left < _length)
158 {
159 large = left;
160 }
161 else
162 {
163 break;
164 }
165
166 if (_items[large].CompareTo(top) <= 0)
167 {
168 break;
169 }
170
171 _items[current] = _items[large];
172 current = large;
173 }
174
175 _items[current] = top;
176 }
177
178 public bool IsFull()
179 {
180 return _length == _items.Length;
181 }
182
183 public bool IsEmpty()
184 {
185 return _length == 0;
186 }
187 }
188 }
189 }
下篇简单的介绍一下堆排序。























