【心电信号】基于matlab心电信号特征提取+分析处理【含Matlab源码 289期】

原创

佛怒火莲 2022-04-11 18:37:23 博主文章分类：matlab完整代码 ©著作权

文章标签 matlab 开发语言算法维纳滤波 sed 文章分类 数据挖掘人工智能

©著作权归作者所有：来自51CTO博客作者佛怒火莲的原创作品，请联系作者获取转载授权，否则将追究法律责任

二、心电信号简介

0 引言

心电信号是人类最早研究的生物信号之一, 相比其他生物信号更易于检测, 且具有直观的规律。心电图的准确分析对心脏病的及早治疗有重大的意义。人体是一个复杂精密的系统, 有许多不可抗的外界因素, 得到纯净的心电信号非常困难。可以采用神经网络算法去除心电信号的噪声, 但这种方法存在训练难度大、耗时长的缺点。小波变换在处理非线性、非平稳且奇异点较多的信号时具有一定的优越性, 近年来许多学者使用其对心电信号进行研究。

1 心电信号简介

心电信号由以下几个波段组成, 一个典型的心电图如图1所示。

【心电信号】基于matlab心电信号特征提取+分析处理【含Matlab源码 289期】_开发语言

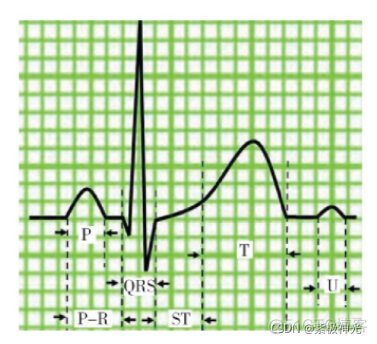
图1 典型心电图

(1) P波:反映心房肌在除极过程中的电位变化过程;

(2) P-R间期:反映的是激动从窦房结通过房室交界区到心室肌开始除极的时限;

(3) QRS波群:反映心室肌除极过程的电位变化;

(4) T波:代表心室肌复极过程中所引起的电位变化;

(5) S-T段:从QRS波群终点到达T波起点间的一段水平线[2];

(6) Q-T间期:心室从除极到复极的时间[3];

(7) U波:代表动作电位的后电位。

由于心电信号十分微弱, 且低频, 极易受到干扰, 不同的干扰源的噪声虽是随机的, 但来自同一个干扰源的噪声往往具有同一类特征。分析干扰的来源, 针对不同的来源使用合适的处理方法, 是数据采集重点考虑的一个问题。常见干扰有3种: (1) 工频干扰; (2) 基线漂移; (3) 肌电干扰。其中已经证明小波变换在抑制心电信号的工频干扰方面具有较大优势。具体噪声频带如表1所示。

表1 心电信号以及主要噪声频带

【心电信号】基于matlab心电信号特征提取+分析处理【含Matlab源码 289期】_算法_02

三、部分源代码

clear
Fs=360;N=2048;
load('9.mat');
x1=y;
load('11.mat');
x2=y;
figure
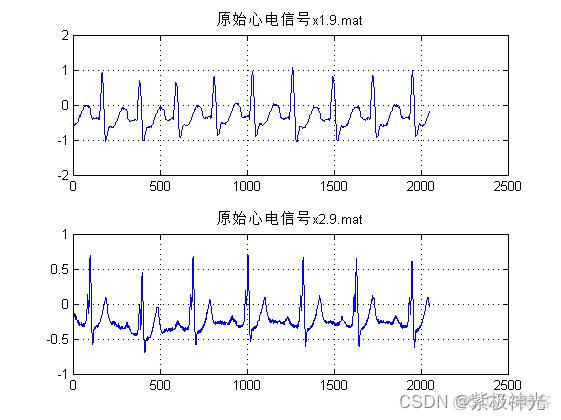
subplot(2,1,1);plot(x1);grid;title('原始心电信号x1.9.mat');
subplot(2,1,2);plot(x2);title('原始心电信号x2.9.mat');grid
%(1)谱分析 
plot(f1,mag1);axis([0,370,0,190]);grid;      %画出频谱图  
xlabel('频率(HZ)');ylabel('幅值');title('心电信号x1幅度谱'); 
figure  
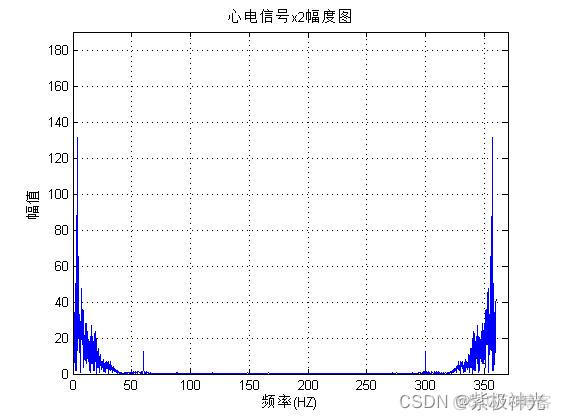
plot(f2,mag2);axis([0,370,0,190]);grid;      %画出频谱图  
xlabel('频率(HZ)');ylabel('幅值');title('心电信号x2幅度图'); 
figure
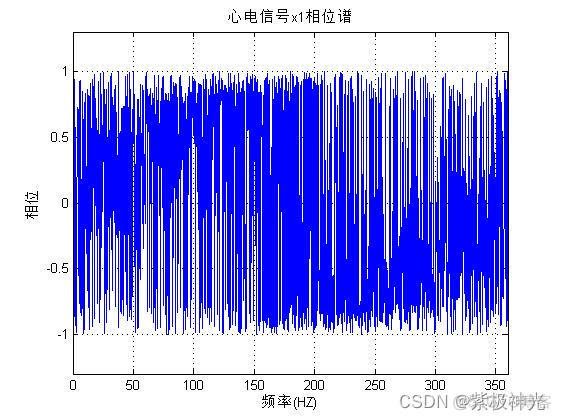
plot(f1,angle(mf1)/pi);axis([0 360 -1.3 1.3]);grid;
xlabel('频率(HZ)');ylabel('相位');title('心电信号x1相位谱'); 
figure
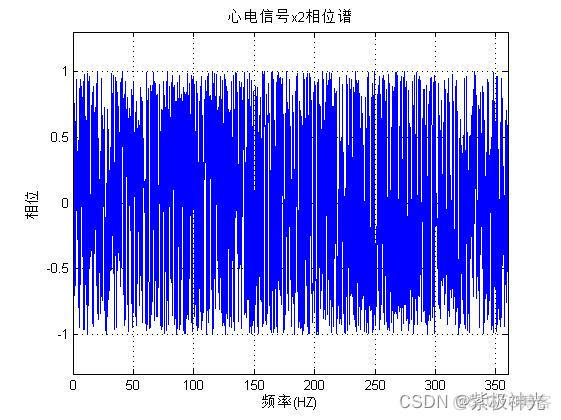
plot(f1,angle(mf2)/pi);axis([0 360 -1.3 1.3]);grid;
xlabel('频率(HZ)');ylabel('相位');title('心电信号x2相位谱'); 

wn1=x1;
wn2=x2;
P1=10*log10(abs(fft(wn1).^2)/N);
P2=10*log10(abs(fft(wn2).^2)/N);
f1=(0:length(P1)-1)/length(P1);  
f2=(0:length(P2)-1)/length(P2);  
figure  
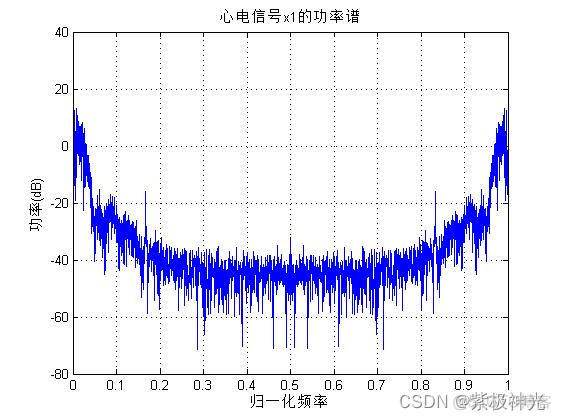
plot(f1,P1);grid  
xlabel('归一化频率');ylabel('功率(dB)');title('心电信号x1的功率谱');  
figure  
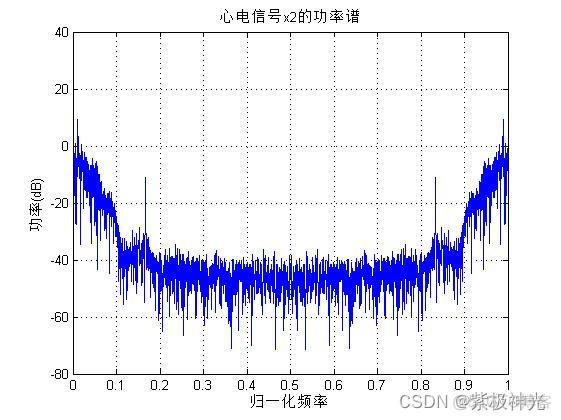
plot(f2,P2);grid  
xlabel('归一化频率');ylabel('功率(dB)');title('心电信号x2的功率谱');  
%（2）相关分析
avr1=mean(x1);avr2=mean(x2);
fprintf('信号x1的均值= %f\n',avr1);fprintf('信号x2的均值= %f\n',avr2);
var1=var(x1);var2=var(x2);
fprintf('信号x1的方差= %f\n',var1);fprintf('信号x2的方差= %f\n',var2);
rx1=xcorr(x1,'biased');
rx2=xcorr(x2,'biased');
rx1x2=xcorr(x1,x2);
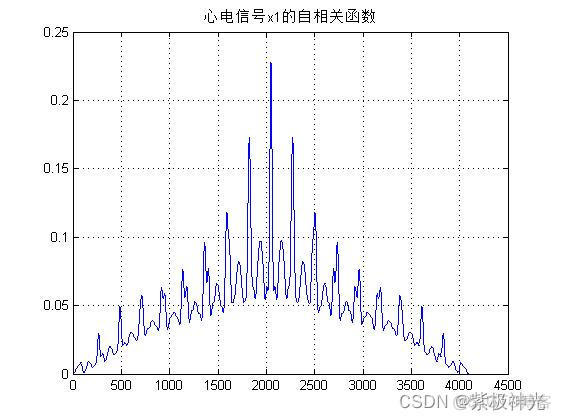
figure
plot(rx1);grid;title('心电信号x1的自相关函数');
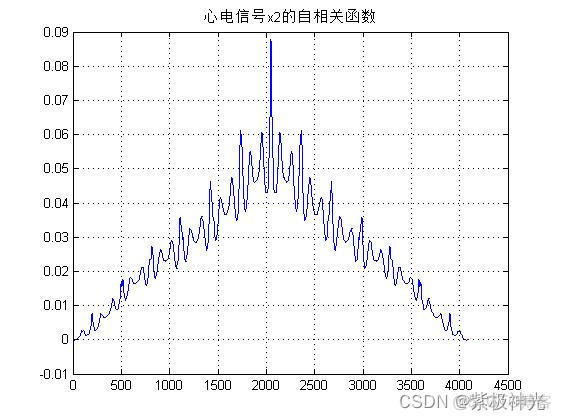
figure
plot(rx2);grid;title('心电信号x2的自相关函数');
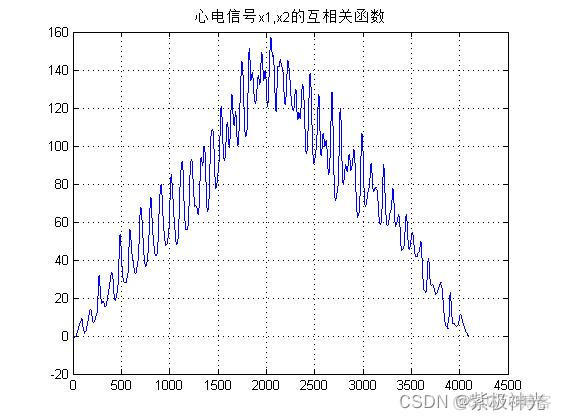
figure
plot(rx1x2);grid;title('心电信号x1,x2的互相关函数');
%(3)数字滤波器设计
SNR=10*log(100/8); % 2%是能量比
x11=awgn(x1,SNR);
figure
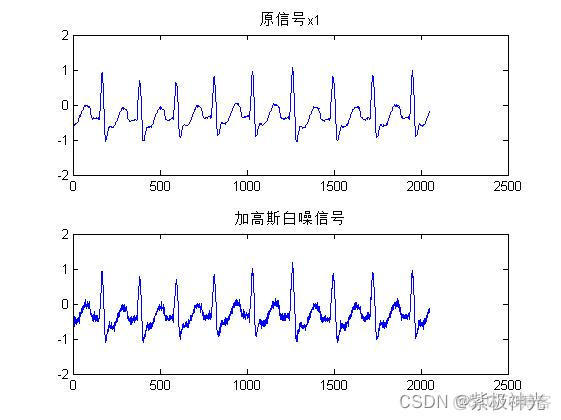
subplot(2,1,1), plot(x1);title('原信号x1');% 加入噪声后有毛刺,但2%的噪声有点小,毛刺不明显。
subplot(2,1,2), plot(x11);title('加高斯白噪信号');

dt=1/1023.5; % 取樣時距(或週期),sec
t=(0:dt:2)'; % 建立一個0-2秒的時間向量
y_high=sin(2*pi*1000*t)/10; % 100 Hz的高頻訊號,振福1/10
y_out=x1+y_high; % 基頻載上一組高頻的輸出。
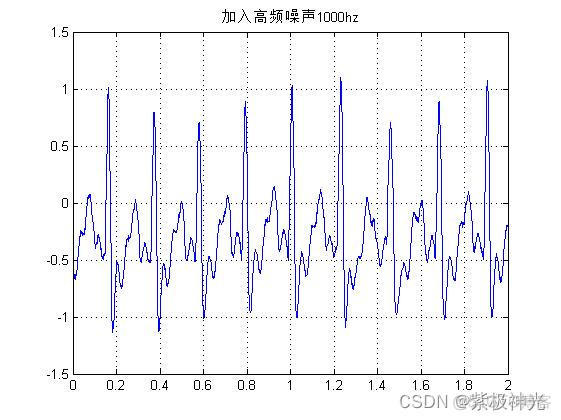
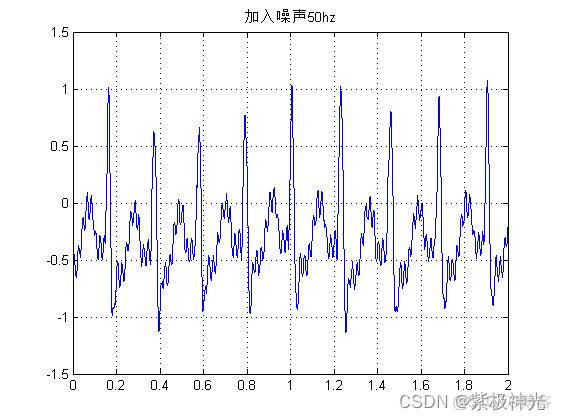
figure
plot(t,y_out);grid;title('加入高频噪声1000hz');

%——————IIR零相移数字滤波器纠正基线漂移——————-  
Wp=1.4*2/Fs;     %通带截止频率   
Ws=0.6*2/Fs;     %阻带截止频率   
devel=0.005;    %通带纹波   
Rp=20*log10((1+devel)/(1-devel));   %通带纹波系数    
Rs=20;                          %阻带衰减   
[N, Wn]=ellipord(Wp,Ws,Rp,Rs,'s');   %求椭圆滤波器的阶次   
[b, a]=ellip(N,Rp,Rs,Wn,'high');       %求椭圆滤波器的系数   
[hw,w]=freqz(b,a,512);     
result =filter(b,a,x1);   
  
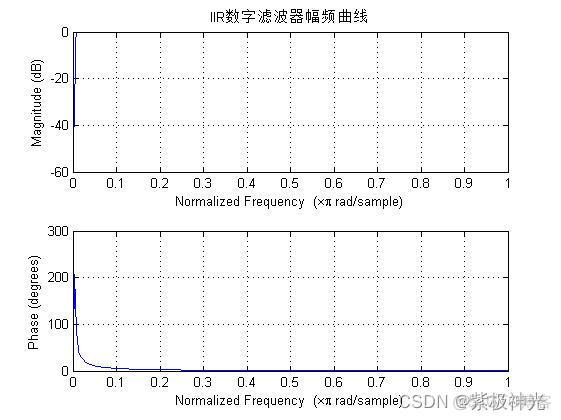
figure  
freqz(b,a);title('IIR数字滤波器幅频曲线');  
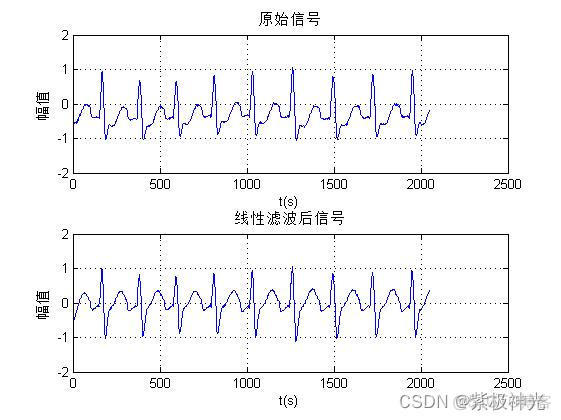
figure;subplot(2,1,1); plot(x1);   
xlabel('t(s)');ylabel('幅值');title('原始信号');grid  
subplot(2,1,2); plot(result);   
xlabel('t(s)');ylabel('幅值');title('线性滤波后信号');grid  
    
figure  
N=512; 
subplot(2,1,1);plot(abs(fft(x1))*2/N);  
xlabel('频率(Hz)');ylabel('幅值');title('原始信号x1频谱');grid;  
subplot(2,1,2);plot(abs(fft(result))*2/N);  
xlabel('频率(Hz)');ylabel('幅值');title('线性滤波去掉基线漂移频谱');grid;
%（5）维纳滤波器去除工频干扰：

%维纳滤波
Mlag=100;
N=100;%维纳滤波器长度
Rxn=xcorr(x_noise,Mlag,'biased');
Rxnx=xcorr(x1,x_noise,Mlag,'biased');%产生输入信号与原始信号的互相关函数
rxnx=zeros(N,1);
rxnx(:)=Rxnx(101:101+N-1);
Rxx=zeros(N,N);%产生输入信号自相关矩阵
Rxx=diag(Rxn(101)*ones(1,N));
for i=2:N
c=Rxn(101+i)*ones(1,N+1-i);
Rxx=Rxx+diag(c,i-1)+diag(c,-i+1);
end
Rxx;
h=zeros(N,1);     
h=inv(Rxx)*rxnx;    %计算维纳滤波器的h(n) 
yn=filter(h,1,x_noise);   %将输入信号通过维纳滤波器 
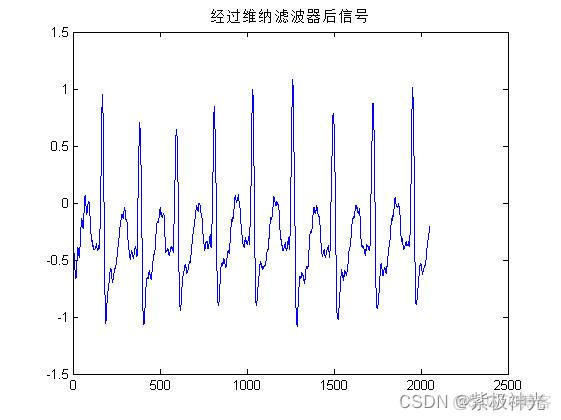
figure        
plot(yn);title('经过维纳滤波器后信号');   
ynmean=mean(yn) %计算经过维纳滤波器后信号均值 
ynms=mean(yn.^2)  %计算经过维纳滤波器后信号均方值  
ynvar=var(yn,1) %计算经过维纳滤波器后信号方差 
Ryn=xcorr(yn,Mlag,'biased');  % 计算经过维纳滤波器后信号自相关函数     
Y=fft(yn);    %计算经过维纳滤波器后信号序列的快速离散傅里叶变换       
Y1=fft(x_noise);
Py=Y.*conj(Y)/600;  % 计算信号频谱  
Py1=Y.*conj(Y)/600;
figure
subplot(211)      
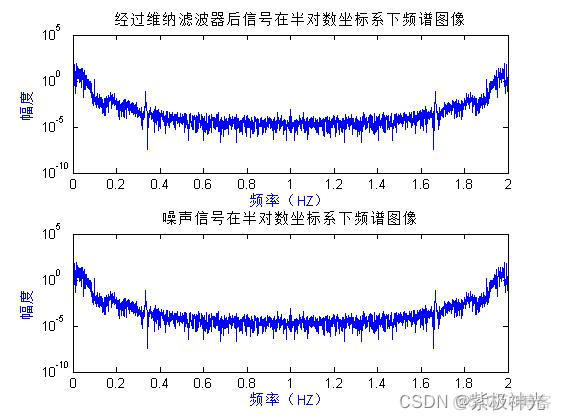
semilogy(t,Py)  %绘制在半对数坐标系下频谱图像 
title('经过维纳滤波器后信号在半对数坐标系下频谱图像')
xlabel('频率（HZ）','color','b');ylabel('幅度','color','b')
subplot(212)      
semilogy(t,Py1) %绘制在半对数坐标系下频谱图像 
title('噪声信号在半对数坐标系下频谱图像')
xlabel('频率（HZ）','color','b');ylabel('幅度','color','b')
pyn=periodogram(yn);%计算经过维纳滤波器后信号的功率谱密度
pyn1=periodogram(x_noise);
figure
subplot(211)
semilogy(pyn)%绘制在半对数坐标系下功率谱密度图像
title('经过维纳滤波器后信号在半对数坐标系下功率谱密度图像');
xlabel('频率','color','b');ylabel('幅度','color','b')
subplot(212)
semilogy(pyn);title('噪声信号在半对数坐标系下功率谱密度图像');
xlabel('频率','color','b');ylabel('幅度','color','b')