一、粒子群算法
粒子群算法( Particle Swarm Optimization, PSO)最早是由Eberhart和Kennedy于1995年提出,它的基本概念源于对鸟群觅食行为的研究。设想这样一个场景:一群鸟在随机搜寻食物,在这个区域里只有一块食物,所有的鸟都不知道食物在哪里,但是它们知道当前的位置离食物还有多远。最简单有效的策略?寻找鸟群中离食物最近的个体来进行搜素。PSO算法就从这种生物种群行为特性中得到启发并用于求解优化问题。
用一种粒子来模拟上述的鸟类个体,每个粒子可视为N维搜索空间中的一个搜索个体,粒子的当前位置即为对应优化问题的一个候选解,粒子的飞行过程即为该个体的搜索过程.粒子的飞行速度可根据粒子历史最优位置和种群历史最优位置进行动态调整.粒子仅具有两个属性:速度和位置,速度代表移动的快慢,位置代表移动的方向。每个粒子单独搜寻的最优解叫做个体极值,粒子群中最优的个体极值作为当前全局最优解。不断迭代,更新速度和位置。最终得到满足终止条件的最优解。
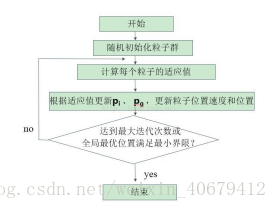
算法流程如下:
1、初始化
首先,我们设置最大迭代次数,目标函数的自变量个数,粒子的最大速度,位置信息为整个搜索空间,我们在速度区间和搜索空间上随机初始化速度和位置,设置粒子群规模为M,每个粒子随机初始化一个飞翔速度。
2、 个体极值与全局最优解
定义适应度函数,个体极值为每个粒子找到的最优解,从这些最优解找到一个全局值,叫做本次全局最优解。与历史全局最优比较,进行更新。
3、 更新速度和位置的公式

![]()
![]()
4、 终止条件
(1)达到设定迭代次数;(2)代数之间的差值满足最小界限
![]()
以上就是最基本的一个标准PSO算法流程。和其它群智能算法一样,PSO算法在优化过程中,种群的多样性和算法的收敛速度之间始终存在着矛盾.对标准PSO算法的改进,无论是参数的选取、小生境技术的采用或是其他技术与PSO的融合,其目的都是希望在加强算法局部搜索能力的同时,保持种群的多样性,防止算法在快速收敛的同时出现早熟收敛。
二、蝴蝶算法
蝴蝶优化算法(butterfly optimization algorithm, BOA)是Arora 等人于2019年提出的一种元启发式智能算法。该算法受到了蝴蝶觅食和交配行为的启发,蝴蝶接收/感知并分析空气中的气味,以确定食物来源/交配伙伴的潜在方向。
蝴蝶利用它们的嗅觉、视觉、味觉、触觉和听觉来寻找食物和伴侣,这些感觉也有助于它们从一个地方迁徙到另一个地方,逃离捕食者并在合适的地方产卵。在所有感觉中,嗅觉是最重要的,它帮助蝴蝶寻找食物(通常是花蜜)。蝴蝶的嗅觉感受器分散在蝴蝶的身体部位,如触角、腿、触须等。这些感受器实际上是蝴蝶体表的神经细胞,被称为化学感受器。它引导蝴蝶寻找最佳的交配对象,以延续强大的遗传基因。雄性蝴蝶能够通过信息素识别雌性蝴蝶,信息素是雌性蝴蝶发出的气味分泌物,会引起特定的反应。
通过观察,发现蝴蝶对这些来源的位置有非常准确的判断。此外,它们可以辨识出不同的香味,并感知它们的强度。蝴蝶会产生与其适应度相关的某种强度的香味,即当蝴蝶从一个位置移动到另一个位置时,它的适应度会相应地变化。当蝴蝶感觉到另一只蝴蝶在这个区域散发出更多的香味时,就会去靠近,这个阶段被称为全局搜索。另外一种情况,当蝴蝶不能感知大于它自己的香味时,它会随机移动,这个阶段称为局部搜索。
香味
为了理解BOA中的香味是如何计算的,首先需要理解,像气味、声音、光、温度等这样的模态是如何计算的。感知、处理这些模态需要知道三个重要的术语:感觉模态C、刺激强度I和幂指数a。在感觉模态中,感觉意味着测量能量的形式并以类似方式对其进行处理,而模态是指传感器使用的原始输入。不同的形态可以是气味,声音,光线,温度,在BOA中,模态是香味。I是物理刺激的大小。在BOA中,I与蝴蝶/解决方案的适应度相关。这意味着,当一只蝴蝶散发出更多的香味时,周围的其他蝴蝶可以感知到并被吸引。幂是强度增加的指数。参数a允许正则表达式、线性响应和响应压缩。响应扩展是当I增加时,香味(f)比I增长更快。响应压缩是当I增加时,f比I增长慢。线性响应是当I增加时,f成比例地增加。经实验证明,有时随着刺激的增强,昆虫对刺激变化的敏感性变得越来越低。因此在BOA中,为了估计I的大小,使用了响应压缩。
蝴蝶的自然现象基于两个重要问题:I的变化和f的表示。简单地说,蝴蝶的I与编码后的目标函数相关联。但是,f是相对的,即应该由其他蝴蝶来感知。史蒂文斯幂定律中,为了将气味与其他形式区别开来,使用了C。现在,当I较少的蝴蝶向I较多的蝴蝶移动时,f比I增加得更快。因此,我们应该允许f随幂指数参数a实现的吸收程度而变化。在BOA中,香味被表示为刺激物的物理强度的函数,如下所示:
![]() .
.
其中f为香味的大小,即其他蝴蝶感知到的香味强度,c 为感官模态,在[0,1]之间取值;I 为刺激强度;a 为幂指数,在[0,1]之间取值。在一个极端情况下,a=1,意味着一只特定蝴蝶发出的香气量被其他蝴蝶以同样的能力感知到,这相当于说香味是在理想化的环境中传播的,在这个区域的任何地方都可以感觉到一只散发着香味的蝴蝶。因此,可以很容易地达到单个(通常是全局的)最优值。另一方面,如果a=0,这意味着任何一只蝴蝶散发出的香味都不会被其他蝴蝶感觉到。所以,参数a控制算法的行为。另一个重要参数是c,它也是决定BOA算法收敛速度和性能的关键参数。理论上c∈[0,∞],但实际上是由待优化系统的特性决定的。A和c的取值对算法的收敛速度有重要影响。在最大化问题中,强度可以与目标函数成正比。
具体算法
为了用搜索算法演示上述讨论,将蝴蝶的上述特征理想化如下:
1.所有的蝴蝶都可以发出气味,这使蝴蝶间相互吸引。
2.每只蝴蝶都会随机移动或朝最好的蝴蝶移动,散发出更多的芳香。
3. 蝴蝶的刺激强度受目标函数的景观影响或决定。
该算法分为三个阶段:(1)初始化阶段、(2)迭代阶段和(3)结束阶段。
在BOA的每次运行中,首先执行初始化阶段,然后进行迭代搜索,最后在找到最优解时终止算法。BOA中使用的参数值也会被分配,设置这些值后,算法将继续创建初始蝴蝶种群以进行优化。由于在BOA的模拟过程中蝴蝶总数保持不变,分配了一个固定大小的内存来存储信息。蝴蝶的位置是在搜索空间中随机生成的,并计算和存储它们的香味和适应值。这样就完成了初始化阶段,算法开始了迭代阶段,该阶段使用创建的人工蝶形执行搜索。算法的第二阶段,即迭代阶段,由算法执行多次迭代。在每次迭代中,解空间中的所有蝶形都移到新位置,然后重新评估其适应性值。算法首先计算解空间中不同位置的所有蝴蝶的适应度值。那么这些蝴蝶就会利用式1在自己的位置产生香味。该算法有两个关键步骤,即全局搜索阶段和局部搜索阶段。在全局搜索阶段,蝴蝶向最合适的蝴蝶/解g∗迈出一步,该蝴蝶/解g可以用公式(2)来表示。
![]()
这里,g∗表示在当前迭代的所有解中找到的当前最佳解;fi表示第i只蝴蝶的香味,r是[0,1]中的随机数。局部搜索阶段可以表示为
![]()
其中,xjt和xkt是解空间中的第j个蝴蝶和第k个蝴蝶。
蝴蝶寻找食物、交配伙伴可以在局部和全局范围内发生。考虑到地理上的接近和各种其他因素,如雨、风等,在整个交配伙伴或蝴蝶的觅食活动中,寻找食物可能占很大比例。因此,在BOA中使用切换概率p来在普通全局搜索和密集局部搜索之间切换。
在未达到停止标准之前,一直进行迭代。迭代结束的标准可以有多个,如使用的最大CPU时间、达到的最大迭代次数、没有改进的最大迭代次数、达到错误率的特定值或任何其他适当的标准。当迭代阶段结束时,算法输出具有最佳适应度的最优解。
三、基于粒子群的混沌混合蝴蝶优化算法



![]()

![]()
四、部分代码
%___________________________________________________________________________________________ %
% The HPSOBOA source codes v2.0 %
% %
%___________________________________________________________________________________________ %
clear
clc
close all
warning off all
SearchAgents_no = 30; % Number of search agents
Max_iteration = 500; % Maximum number of iterations
Function_name='F3'; %F1-F15,US(Unimodal Separable);F16-F26,MS(Multimodal Separable)
%%% Exp2: F1,F2,F4, F6, F15, F17 ,F18
%US: F1,F2,F4,F6,F11, MS: F15, F17, F18, F24, F25
%%%%% BOA in 2018
[lb,ub,dim,fobj]=Hight_Get_Functions_details(Function_name);
[Best_scoreBOA,Best_pos,BOA_cg_curve]=BOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
%%%% PSOBOA in 2020
[Best_score_PSOBOA,Best_pos_PSOBOA,PSOBOA_cg_curve]=PSOBOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
%%%% HPSOBOA in 2020
[Best_score_HPSOBOA,Best_pos_HPSOBOA,HPSOBOA_cg_curve]=HPSOBOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
%%%% plots
figure('Position',[500 400 800 200]) %[left bottom width height]
subplot(1,2,1);
func_plot_con(Function_name);
title(Function_name)
% xlabel('x_1');
% ylabel('x_2');
% zlabel([Function_name,'( x_1 , x_2 )'])
%%%%%% Convergence curves
subplot(1,2,2);
semilogy(BOA_cg_curve,'b-','LineWidth',1)
hold on
semilogy(PSOBOA_cg_curve,'g-','LineWidth',1)
hold on
semilogy(HPSOBOA_cg_curve,'r-','LineWidth',1)
% axis tight
% grid off
xlabel('Iterations');
ylabel('Fitness value');
legend('BOA','PSOBOA','HPSOBOA')
五、仿真结果


六、参考文献
[1] Arora S, Singh S. Butterfly optimization algorithm: a novel approach for global optimization[J]. Soft Computing. 2019, 23(3): 715-734.

![]()