AI 高等数学、概率论基础

一、概论

　　基础引入：

　　　　

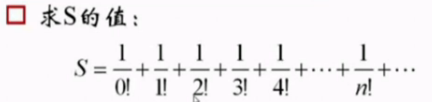
　　原理一：【两边夹定理】

　　　　

　　原理二：【极限】

　　　　　　　　

　　　　X为角度x对应的圆弧的点长；

　　原理三【单调性】：

　　　　

　　引入：

　　 　　　

二、导数

　　　　　

　　常见函数的导数：

　　　　

四、应用：

　　　　

　　求解：

　　　　

　　泰勒展式和麦克劳林展式：

　　　　

　　泰勒展式在x0 = 0处展开得到麦克劳林展式

　　Taylor公式的应用1：

　　　　

　　变种：

　　　　

　　Taylor公式应用2：

　　　　

　　方向导数：

　　　

　　梯度：

　　　　

　　函数的凸凹性：

　　　　

　　函数凸凹性判定：

　　　　

　　

　　凸函数性质的应用：

　　　　、

　　　　

五、概率论

　　

 

　　概率为0例子： 把一枚针投在一个平面上，则概率为0（一个点 之于 一个面）

　　古典概型：

　　　　

　　　　思路：

　　　　　　

　　　　　　

　　古典概型变种问题：

　　　　生日悖论：

　　　　

　　　　

　　古典概型总结：

　　　　

　　几何概型：

　　　

　　　　

　　条件概率：

　　　　

　　条件概率： 在已知B发送的条件下，A发生的概率

　　　　　　

　　全概率：

　　　　

　　　　全概率公式的意义在于： 当直接计算P（A）比较困难，而P(B_i),P(A|B_i)  (i=1,2,...)的计算较为简单时，可以利用全概率公式计算P(A)。思想就是，将事件A分解成几个小事件，通过求小事件的概率，然后相加从而求得事件A的概率，而将事件A进行分割的时候，不是直接对A进行分割，而是先找到样本空间Ω的一个个划分B₁,B₂,...B_n,这样事件A就被事件AB₁,AB₂,...AB_n分解成了n部分，即A=AB₁+AB₂+...+AB_n, 每一B_i发生都可能导致A发生相应的概率是P(A|B_i)，由加法公式得

         P(A)=P(AB₁)+P(AB₂)+....+P(AB_n)

               =P(A|B₁)P(B₁)+P(A|B₂)P(B₂)+...+P(A|B_n)P(PB_n)

　　贝叶斯公式：

　　　　与全概率公式解决的问题相反，贝叶斯是建立在条件概率的基础上寻找事件发生的原因（即大事件A已经发生的条件下，分割中的小事件Bi的概率），设B₁,B₂,...是样本空间Ω的一个划分，则对任一事件A（P(A)>0),有

　　　　　　

　　　　　　　　B_i 常被视为导致试验结果A发生的”原因“，P(B_i)(i=1,2,...)表示各种原因发生的可能性大小，故称先验概率；P(B_i|A)(i=1,2...)则反映当试验产生了结果A之后，再对各种原因概率的新认识，故称后验概率。

　　　贝叶斯公式的应用：

　　　　

 　　　　、

　　两学派的认知：【频率学派 && 贝叶斯学派】

　　　　

　　贝叶斯公式扩展：

　　　　

　　两点分布：

　　　　

　　二项分布：【伯努力分布】

　　　　

　　泊松分布【Taylor展式结合】：

　　　　

　　　　

 

　　泊松分布的应用：

　　　　

　　连续分布之均匀分布：

　　　　

 　　连续分布之指数分布：

　　　　　 

　　指数分布的无记忆性：

　　　　

　　连续分布之正态分布【高斯分布】：

 　　　　

　　总结：

　　　　

　　指数族：

　　　　二项分布【伯努力分布】，正态分布【高斯分布】属于指数族

　　logistic函数【sigmod函数】：

　　　　

　　Logistic函数的导数：

　　　　　

　期望：

　　　　

　　期望的性质：

　　　　

　　　　note： P(xy) = P(x) P(y)   -->  x， y独立

　　方差：

　　　　

　　协方差：

　　　　

　　协方差、独立、不相关关系：

　　　　

　　协方差的意义：

　　　　

　　协方差的上界：

　　　　

　　　　   

　　独立一定不相关，不相关不一定独立，不相关只是线性独立，可能是非线性不独立；

相关系数：

　　　

　　　其中：Var（x）： 标准差；

　协方差矩阵：

　　　　

 　　原点矩 和 中心矩

　　　　

　　　　 期望为一阶原点矩， 方差为2阶中心矩

　概念总结：

　　　　

　　偏度：

　　　　　　　　

　　　　　　偏度为0， 则是正态分布

　　偏度公式：

　　　　　　

　　峰度：

　　　　　　

　　应用：

　　　　

　　　　

　　引入切比雪夫不等式：

　　　　

　　大数定理：

　　　　

　　　　

　　中心极限定理：

　　　　

　　标准的中心极限定理的问题：

　　　　

　　中心极限定理的意义：

　　　　

　　样本的统计量：

　　　　

　　样本的矩：

　　　　

　　随机变量的矩 和 样本的矩， 有什么关系呢？？

　　　　

　　矩估计：【非常重要】

　　　　 

　　正态分布的矩估计：

　　　　

　　均匀分布的矩估计：

　　　　

　　贝叶斯公式带来的思考：

　　　　

　　最大似然估计：

　　　　　　

　　极大似然估计的具体实践：

　　　　　　

　　极大似然估计的应用：

　　　　  

　　正态分布的极大似然估计：

　　　　

　　　　    

　　　　

　　总结：

　　　　

　　极大似然估计与过拟合：

　　　　

　　　　5、 10 为超参数；