树的概念本身是比较简单的,绝大部分情况下,我们都不会讨论树这个大类,而是具体的某种类型的树,比如各种类型的二叉树。在具体的树的类型中,各种不同的应用会根据他们的场景特点选择特定类型的树来处理元素的操作。比如,红黑树,平衡二叉树,AVL平衡二叉树,二叉堆......在此之前,我们需要对一些重要的概念进行比较,重点是比较他们的区别,否则说起某个具体的类型,脑海中可能完全是模糊的。
【树】
树的定义:
(1)每个元素称为节点(node)。
(2)有一个特定的节点被称为根节点或树根(root)。
(3)除根节点之外的其余数据元素被分为个互不相交的集合,其中每一个集合本身也是一棵树,被称作原树的子树(subtree)。
对于节点,根,子树的概念都不陌生。这里重要的概念在于除根节点外,也是互不相交的树,这种分形的定义有点类似递归的概念,直接将树与环区分开来。
树的属性:
对于树,无论是什么类型的树,有几个重要的属性概念,在各种树的讨论中,会被频繁提及,这里进行集中说明:
节点/结点,根节点,父节点,子节点,兄弟节点 -- 这些都很容易理解,不在此说明
叶子节点:度为0,其实就是没有子节点的节点,这里我之前会被"叶"的概念迷惑,但这里就只认他们为普通节点就好,只是没有子节点,不要把它们想得太特殊,这个叶子节点,只是为了区分其它有子节点的节点而进行的区分手段;
节点的度:定义是子节点的个数,这里注意子节点就是严格的只与本节点直接相连的子节点,不要把子节点的下级也算在其中
节点的层次:根在第一层,根的子节点是第二层,后续的类推......
树的深度:树的最大层次
这几个概念需要特别清楚,否则说起来各种类型的树有什么特点,提到度、层次、深度等概念时可能还不清楚,那就无法准确理解后续的表述了。
【二叉树】
这里进入一个比较重要的树的类型了。后续的堆、红黑树、平衡树...都是基于二叉树的概念。
首先,二叉树是一种树。与树不同的是,二叉树的每个节点,最多有2个子节点(即二叉树中不存在度大于2的节点)。二叉树的子树是有顺序的,分为左子树和右子树(之所以要这么区分,是因为后续的场景会在此基础上定义更多细节,从而形成有特殊作用的数据结构),即使只有一颗子树,也是要区分左右的。
总结,最多2个子节点,且除了根节点,每个节点都分为左和右。当节点数n=0时,称为空树。
到了这里,我们可以看看一些常见的二叉树种类:
- 满二叉树
- 完全二叉树
- 完美二叉树
- 二叉查找树
- 平衡二叉树
- 红黑树
- 堆(二叉堆)
【满二叉树】
国内对于满二叉树的定义是,每一层的节点数都达到了最大值,即:1,2,4,...。这样一来,满二叉树的相关属性就是确定的了,节点数为(2^k-1),其中k为层数。第i层上的结点个数为2^(i-1)。
国内满二叉树: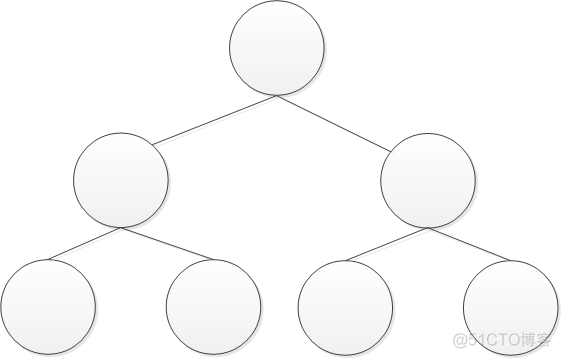
国外对于满二叉树的定义是,要么是叶子节点,要么度为2的节点。这里没有要求每一层达到最大值。而国外对于完美二叉树的定义是跟国内满二叉树的定义一致。
国外满二叉树: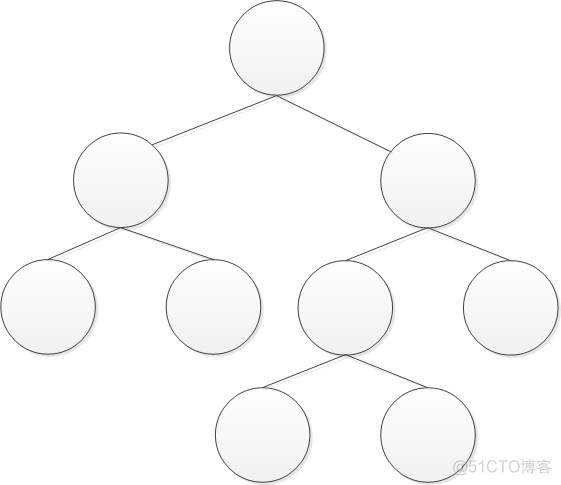
【完全二叉树】
其实前面的满二叉树,也是给后续的场景做铺垫。到这里,很多相关的实用的场景就会高频提及这些概念。完全二叉树是一些重要结构的基础。
1.除去最后一层节点,为完美二叉树。
2.最后一层节点,依次从左往右排列。
根据这个定义,可以看看下图中的二叉树,它们都是完全二叉树:
而对于下图中示例,就不是完全二叉树:
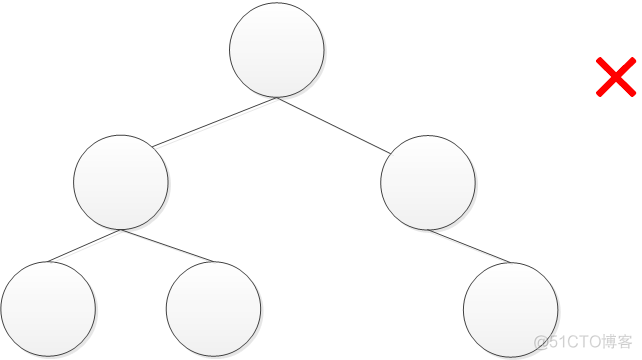
由于完全二叉树的特点,我们可以使用数组进行节点数据的存储,这一特点在一些排序的操作中很常用。























