51nod 1188 最大公约数之和 V2

1188 最大公约数之和 V2

1. 2.0 秒
2.  
3. 262,144.0 KB
4.  
5. 160 分
6.  
7. ​​6级题​​

给出一个数N，输出小于等于N的所有数，两两之间的最大公约数之和。

 

 

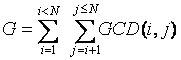
相当于计算这段程序（程序中的gcd(i,j)表示i与j的最大公约数）：

 

G=0;

for(i=1;i<N;i++)

for(j=i+1;j<=N;j++)

{

    G+=gcd(i,j);

}

 收起

输入

第1行：1个数T，表示后面用作输入测试的数的数量。(1 <= T <= 50000) 第2 - T + 1行：每行一个数N。(2 <= N <= 5000000)

输出

共T行，输出最大公约数之和。

输入样例

3 10 100 200000

输出样例

67 13015 143295493160

分析：

简化版

51nod 1040 最大公约数之和 数学+欧拉函数

我们知道每一个与i最大公约数肯定是n的因子，我们枚举n的因子x，然后求满足gcd(n,k)=x的个数即可，相当于求gcd(n/x,k/x)=1(k/x<n/k),即求有多少数与n/x互质,这就需要欧拉函数了。

即变为：i|n代表n%i==0

这题可以化为：

注意第三个等式的j变为i的因子。

到了第三个等式，我们发现题意变为枚举i（i属于[2,n]），然后枚举i的因子j（除了本身）求出答案和，但换个角度我们枚举每一个因子j，放大几倍当作i来使用。

这题需要离线，不离线的话会超时

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MOD=1e9+7;
const ll N=5000055;
int prime[N],mark[N];//prime是素数数组，mark为标记不是素数的数组
ll tot,phi[N];//phi为φ(),tot为1~i现求出的素数个数
void getphi(int N)
{
    phi[1]=1;//φ(1)=1
    for(int i=2; i<=N; i++) //从2枚举到N
    {
        //cout<<i<<" "<<tot<<endl;
        if(!mark[i]) //如果是素数
        {
            prime[++tot]=i;//那么进素数数组，指针加1
            phi[i]=i-1;//根据性质1所得
        }
        for(int j=1; j<=tot; j++) //从现求出素数枚举
        {
            if(i*prime[j]>N)
                break;//如果超出了所求范围就没有意义了
            mark[i*prime[j]]=1;//标记i*prime[j]不是素数
            if(i%prime[j]==0) //应用性质2
            {
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
            else
                phi[i*prime[j]]=phi[i]*phi[prime[j]];//应用性质3
        }
    }
}
ll ans[N],a[50005],sum[N];
int main()
{
    getphi(N-1);
    int n;
    cin>>n;

   for(int i=1;i<=n;i++)
    {
        scanf("%lld",&a[i]);
    }
   
    for(ll i=1; i<=N-1; i++)
    {
        for(ll j=2; i*j<=N-1; j++)
        {
            ans[i*j]+=phi[j]*i;
        }
    }
    for(ll i=1;i<=N;i++)
   {
      sum[i]=ans[i]+sum[i-1];
   }
   for(int i=1;i<=n;i++)
      printf("%lld\n",sum[a[i]]);

    return 0;
}