莫比乌斯反演

莫比乌斯反演

【前言】

初学莫比乌斯反演真是一脸蒙B，查了很多资料，才有点理解。大家一起学习。

【引入】

当满足以下求和函数：

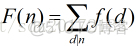
可以得到：

F(1)=f(1)                

F(2)=f(1)+f(2)

F(3)=f(1)+ f(3)          

F(4)=f(1)+f(2)+f(4)                      

F(5)=f(1)+f(5)

推出：

f(1)=F(1)               

f(2)=F(2)-f(1)=F(2)-F(1)

f(3) =F(3)-F(1)          

f(4)=F(4) -f(2)- f(1) =F(4)-F(2)

f(5) =F(5)-F(1)

【定义】

从上面我们可以发现，我们可以通过F[n]推出f[n],满足公式：

 

通俗的来讲：

当d包含相同的质因子p的时候，u(d)=0

当d包含质因子p各不相同的时候，有偶数个质因子，u(d)=1;有奇数个质因子，u(d)=0;

 

如果想看上面性质的具体解释和证明的话：https://wenku.baidu.com/view/fbec9c63ba1aa8114431d9ac.html?from=search

 

而u（d）函数可以通过筛选求出：

void Init()
{
    memset(vis,0,sizeof(vis));
    mu[1] = 1;
    cnt = 0;
    for(int i=2; i<N; i++)
    {
        if(!vis[i])
        {
            prime[cnt++] = i;
            mu[i] = -1;
        }
        for(int j=0; j<cnt&&i*prime[j]<N; j++)
        {
            vis[i*prime[j]] = 1;
            if(i%prime[j]) mu[i*prime[j]] = -mu[i];
            else
            {
                mu[i*prime[j]] = 0;
                break;
            }
        }
    }
}

 

 

【两个重要公式】

【gcd问题】

按顺序看

 

​​HDU 1695​​

 

​​「BZOJ2820」YY的GCD​​