最近刚接触李航博士的《统计学习方法》,还是挺赞的一本书,特别适合机器学习初学者的入门。里面主要阐述机器学习中的几大经典模型的理论方面,包括感知机、kNN、决策树、朴素贝叶斯、逻辑回归、SVM等。下面我结合自己的理解先介绍下感知机及其学习算法,然后通过Python实现这一模型并可视化处理。
1. 感知机模型
f(x)=sign(w⋅x+b)
其中,
x
表示实例的特征向量,
w
表示权值向量,
w⋅x
表示
w
和
x
的内积,计算公式为:
sign为符号函数:
上面几个公式看着比较抽象,下面从几何的角度看下什么是感知机:

从上图可以看到,
w⋅x+b=0
对应于特征空间中的一个超平面(如果特征空间为二维空间,那么超平面为一条直线),该超平面将特征空间划分为正、负两部分。我们要学习得到的感知机模型,就是要求得其中的参数
w
和
x
.
2. 学习算法(原始形式与对偶形式对比)
感知机学习算法是对以下最优化问题的算法. 给定一个训练数据集
}
其中,
xi∈χ=Rn,yi∈{−1,1},i=1,2,⋯,N
,求参数
w,b
,使其为以下损失函数极小化问题的解
其中
M
为误分类点的集合。
关于感知机的损失函数由来以及学习策略这里不再赘述,可以参照《统计学习方法》原著第2章节或者
.
下面我主要从学习算法的原始形式和对偶形式两个方面的对比,来加深该算法的理解。
\ | 原始形式 | 对偶形式 |
输入 | T, 学习率 η(0<η≤1) | T , 学习率 η(0<η≤1) |
输出 | w,b; f(x)=sign(w⋅xi+b) | α,b; f(x)=sign(∑Nj=1αiyixj⋅xi+b) |
误分类条件 | yi(w⋅x+b)≤0 | yi(∑Nj=1αiyixj⋅xi+b)≤0 |
迭代更新 | w←w+ηyixi;b←b+ηyi | αi←αi+η;b←b+ηyi (α,b 初始值为 0 |
区别 | w,b | w,b 表示成 x 和 y 的线性组合的形式,从而得到 w,b |
问1:如何简单地理解学习算法的对偶形式?
通常来说,对于原始形式不好解决的问题,可以转换到对应的对偶形式中,使之更容易求解。比如,在多维空间中运算量较大,感知机学习的对偶形式能够更加简地便计算。
问2:为什么在对偶形式中,迭代更新 α 和 b 能够得到参数 w 和 b 呢?
对偶形式的基本想法是,将 w 和 b 表示为实例 xi 和标记 yi 的线性组合的形式,通过求解其系数而求得 w 和 b现在假设初始值 w0,b0均为 0. 对误分类点 (xi,yi)通过
逐步修改
w,b
. 设修改了
n
次,则
w,b
关于
(xi,yi)
的增量分别是
αiyixi
和
αiyi
,这里
αi=niη
. 最后学习到的
w,b
可以分别表示为
这里,
αi≥0,i=1,2,⋯,N
,当
η=1
时
, αi
当某一个实例点更新的次数越多,意味着它距离分离超平面越近,也就越难分类. 换句话说,这样的实例对学习结果影响最大.
3. 算法实现
x1=(3,3)T,x2=(4,3)T, 负样本点是 x3=(1,1)T,
import numpy as np
x = np.array([[3,3],[4,3],[1,1]])#创建数据集,共3个实例
y = np.array([1,1,-1]) #创建标签
history = [] #存储迭代学习过程中的w,b值,便于可视化绘图
gramMatrix = x.dot(x.T) #计算Gram矩阵,后面需要多次用到
print "gramMatrix = ",gramMatrix
alpha = np.zeros(len(x)) #初始化alpha为零向量
b = 0 #b为回归直线截距
learnRate = 1 #初始化为0;learnRate为学习率,设为1
k = 0; i = 0 #k用来计算迭代次数;i用来判定何时退出while循环
while 1:
if y[i] * (np.sum(alpha * y * gramMatrix[i])+ b)<=0: #误分条件:若某一数据点被错误分类
alpha[i] = alpha[i] + learnRate #更新 alpha 值
b = b + learnRate * y[i] #更新 b 值
i = 0 #i 赋值为0,再遍历一次所有的数据集
k = k + 1 #k + 1 即迭代次数加1
history.append([(alpha * y.T).dot(x), b]) #存储w,b
print "iteration counter =",k
print "alpha = ",alpha
print "b = ", b
continue
else: #若某一数据点被正确分类
i = i + 1
print "i = ",i
if i >= x.shape[0]: #退出while循环条件,即 i >= 3,所有数据点都能正确分类
print "iteration finish"
break #break 退出wile循环
w = (alpha*y.T).dot(x) #计算得到权值 w
print "w = ", w
print "b = ", b
print "history w,b = ",history
#==========================可视化===========================#
import matplotlib.pyplot as plt
from matplotlib import animation
fig = plt.figure()
ax = plt.axes()
line, = ax.plot([], [], 'g', lw=2)
label = ax.text([], [], '')
def init():
global x,y,line,label
plt.axis([-6, 6, -6, 6])
plt.scatter(x[0:2,0],x[0:2,1],c ="r",label = "postive",s = 60) #画正样本点
plt.scatter(x[2,0],x[2,1],c = "y",label = "negtive",s =60) #画负样本点
plt.grid(True)
plt.xlabel('X1')
plt.ylabel('X2')
plt.title('myPerceptron')
return line, label #返回值为line,label对象,表示这两个对象有动画效果
def animate(i): #形参 i 表示帧数,即 animation.FuncAnimation 函数形参列表中的frames属性
global history, ax, line, label
w = history[i][0]
b = history[i][1]
if w[1] == 0: return line, label
x1 = -6.0 #点(x1,y1)和点(x2,y2)确定分类超平面
y1 = -(b + w[0] * x1) / w[1]
x2 = 6.0
y2 = -(b + w[0] * x2) / w[1]
line.set_data([x1, x2], [y1, y2])#画出分类超平面
x1 = 0.0
y1 = -(b + w[0] * x1) / w[1]
label.set_text(str( history[i][0]) + ' ' + str(b)) #在点 (0,y1) 上绘制文本便签
label.set_position([x1, y1])
return line, label
anim = animation.FuncAnimation(fig, animate,init_func=init, frames=len(history), interval=1000, repeat=True,blit=True)
plt.legend(fancybox = True)
plt.show()
#anim.save('perceptron.gif', fps=2, writer='imagemagick') #使用ImageMagick导出GIF图片 实现效果:
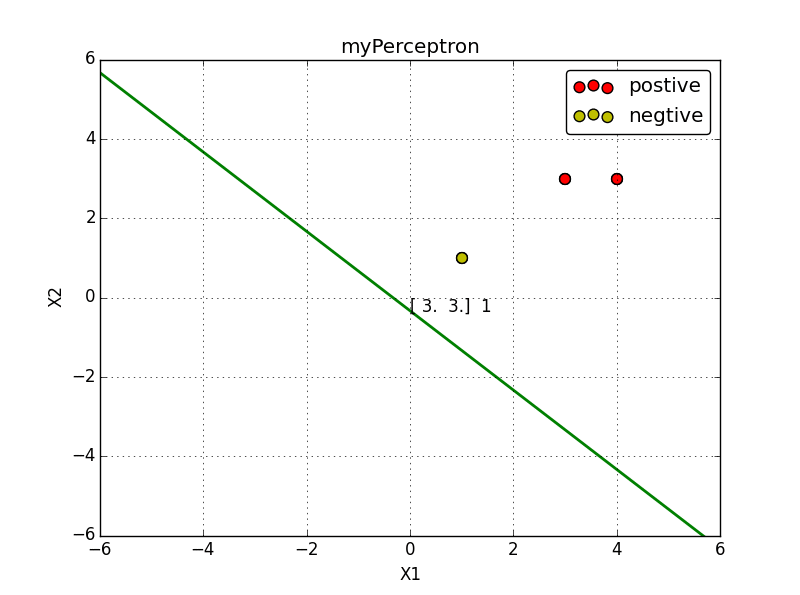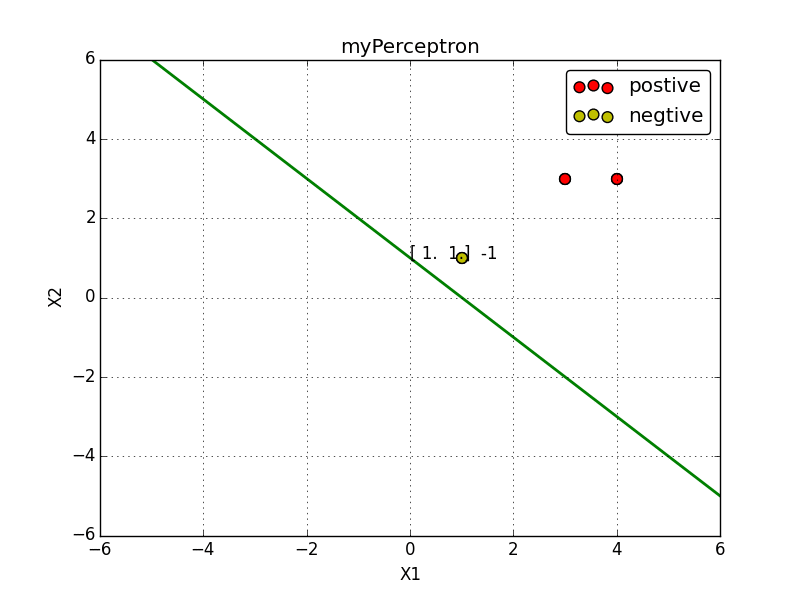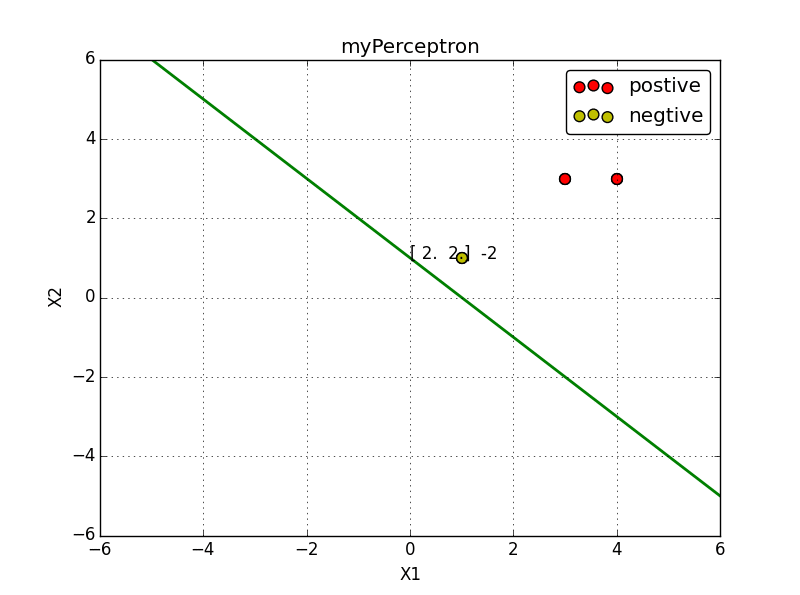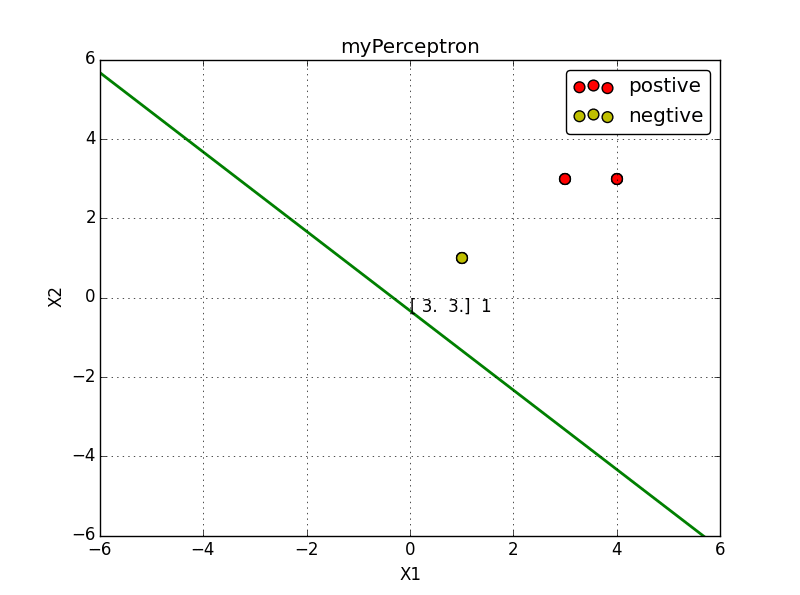
4. 总结
感知机是最简单最基础的分类器,理论也较简单. 但到了真正自己动手实现算法的时候,会遇到各种各样的问题. 说到底还是经验不足,以后有空还是要多推敲推敲代码. 一边实践,一边温习理论知识,理解才会更加深刻.
参考资料:
本文作为个人学习笔记,有什么不正确的地方,还请多多批评指正





















