python中opencv裁剪区域标注越界,会自动调整吗 opencv越线检测

假设1：已经画出拌线，根据 opencv-视频处理--画线（越线、拌线）

假设2：已经检测出运动物体，根据 opencv-视频处理-实时的前景检测-Vibe算法或者其它的前景检测算法

拌线检测(越线检测)，要做的目标就是运动物体（上图中蓝色框）什么时候碰到 越线(拌线)？

【数学表述】：线段和矩形是什么时候相交的？

【问题1】 首先 怎么证明下述两条线段是相交的呢？

假设两条线段,如下图所示：

【答案】只要证明任意一条线段的两个端点在另一条的两侧。

【证明】:我们先证明p1和p2在线段p3p4的两侧。同理可证p3和p4在线段p1p2的两侧。我们只要证明

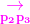
和

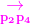
的叉积 和

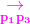
和

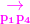
叉积是异号的.

用opencv的程序表示为:

//判断两条线段相交
bool intersection(const vector<Point> & line1, const vector<Point> &line2)//vector<Point> line(2),代表一线段
{
	CV_Assert(line1.size() == line2.size());
	CV_Assert(line1.size()==2);
	Point point1_11,point1_12,point1_21,point1_22;
	//首先判断line1的两个端点,在line2的两侧
	point1_11 = line2[0] - line1[0];
	point1_12 = line2[1]-line1[0];

	point1_21 = line2[0]-line1[1];
	point1_22 = line2[1]-line1[1];

	//point1_11.cross(point1_12)*point1_21.cross(point1_22)<0;//----------表明在两侧
	//再次判断line2的两个端点，在line1的两侧
	Point point2_11,point2_12,point2_21,point2_22;

	point2_11 = line1[0]-line2[0];
	point2_12 = line1[1] - line2[0];
	
	point2_21 = line1[0] -line2[1];
	point2_22 = line1[1]-line2[1];
	
	//point2_11.cross(point2_12)*point2_21.cross(point2_22)<0;
	return ( point1_11.cross(point1_12)*point1_21.cross(point1_22)<0 && point2_11.cross(point2_12)*point2_21.cross(point2_22)<0 );
}

---------------------------------------------------------------------------------------------

【问题2】怎么证明线段和矩形是相交的呢？

【答案】只要证明线段和矩形的任意一条线段即可，根据【问题1】的回答，或者整个线段都在矩形内部

用图表示为：

  

用opencv的程序可以表示为：

//判断矩形和一条线段相交(线段只要与矩形的一条边相交，就可以判定相交 或者 线段在矩形内部)
bool rect_line_intersection(const vector<Point> & line,const Rect & targetRect)//rect的四个顶点(roi.x,roi.y),(roi.x,roi.y+roi.height-1),(roi.x+roi.width-1,roi.y),(roi.x+roi.width-1,roi.y+roi.height-1)
{
	CV_Assert(line.size()==2);
	//先判断第一种情况：线段在矩形内部
	if(line[0].inside(targetRect) && line[1].inside(targetRect))
		return true;
	//再判断第二种情况,线段和矩形的至少一条边相交
	//---第一步：提取矩形的四条边
	vector<Point> line1;
	line1.clear();
	line1.push_back(Point(targetRect.x,targetRect.y));
	line1.push_back(Point(targetRect.x,targetRect.y+targetRect.height-1));
	if(intersection(line1,line))
		return true;
	vector<Point> line2;
	line2.clear();
	line2.push_back(Point(targetRect.x+targetRect.width-1,targetRect.y));
	line2.push_back(Point(targetRect.x+targetRect.width-1,targetRect.y+targetRect.height -1));
	if( intersection(line2,line))
		return true;
	vector<Point> line3;
	line3.clear();
	line3.push_back(Point(targetRect.x,targetRect.y));
	line3.push_back(Point(targetRect.x+targetRect.width-1,targetRect.y));
	if(  intersection(line3,line))
		return true;
	vector<Point> line4;
	line4.clear();
	line4.push_back(Point(targetRect.x,targetRect.y+targetRect.height-1));
	line4.push_back(Point(targetRect.x+targetRect.width-1,targetRect.y+targetRect.height-1));
	if(  intersection(line2,line) )
		return true;
	//return ( intersection(line1,line) || intersection(line2,line)||intersection(line3,line)||intersection(line4,line) );
	return false;
}