贝叶斯模型

动态贝叶斯网络的python实现_H2

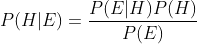
，二分类中展开为

动态贝叶斯网络的python实现_动态贝叶斯网络的python实现_02

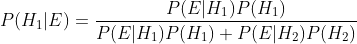
  • P(H) – 已知的先验概率
  • P(H|E) – 我们想求的后验概率，即在B事件发生后对于事件A概率的评估
  • P(E|H) – 在事件H下观测到E的概率
  • P(E) – marginal likelihood(边际似然)，对于所有的假设都是相同的，因此不参与决定不同假设的相对概率
  • P(E|H)/P(E) – likelihood function(可能性函数)，这是一个调整因子，通过不断的获取信息，可以使得预估概率更接近真实概率

贝叶斯推断的举例理解：

在分类问题中，以神奇宝贝为例，有一群神奇宝贝样本，要将其分成水系H1和非水系H2两种。

首先，可以根据已有数据得到一个关于水系宝贝比例，这是一个先验概率，记为P(H1)；

其次，神奇宝贝具有攻击力等多种特征，这里以一个特征为例，得到每个水系样本在该特征值的分布情况，进而得出水系样本的该特征的概率分布情况。具体步骤为：比如使用高斯分布，假设他们的特征分布近似于均值

动态贝叶斯网络的python实现_H2_03

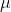
，方差为

动态贝叶斯网络的python实现_动态贝叶斯网络的python实现_04

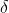
的高斯分布，进而使用maximum likelyhood估计出水系样本可能的概率分布；

然后，根据上述概率分布，可以在给定任何一个新样本（特征）的时候，得到条件概率：在水系中，该特征值出现的概率P(E|H1)；

最后，求P(E)，表示出现该特征值的整体概率，它包括所有样本下的概率，P(E|H1)P(H1)+P(E|H2)P(H2)，求解方法与上面类似。

经过此步骤之后，获得任意一个新样本（设其特征值为E1），我门都可以得到该特征值E1情况下，属于水系宝贝的概率。

朴素贝叶斯理解：

上述例子中，只考虑了一个特征的情况，在多个特征的情况下，我们需要考虑联合概率分布的情况，即：每一个分类下，样本在多个特征组成的多维空间的分布情况。朴素贝叶斯假设多维特征相互独立，因此，简化了联合概率分布的模型（直接将样本在各维空间的概率分布相乘即可）。