拓端tecdat|R语言编程指导对巨灾风险下的再保险合同定价研究案例：广义线性模型和帕累托分布Pareto distributions分析

R语言对巨灾风险下的再保险合同定价研究案例：广义线性模型和帕累托分布Pareto distributions分析

 

 

---

本文为非人寿保险课程的一部分，该示例对1900 -2005年间的“ 美国标准化飓风损失 ”数据集进行研究（2008），我们使用了广义线性模型和帕累托分布Pareto distributions分析。该数据集以xls格式提供，首先我们来导入它，

数据导入和清理

> library(gdata)
> db=read.xls(data.xls",sheet=1)

excel电子表格的问题在于某些列可能具有预先指定的格式（例如，损失为000,000,000格式）

> tail(db)
    Year Hurricane.Description State Category Base.Economic.Damage
202 2005                 Cindy    LA        1          320,000,000
203 2005                Dennis    FL        3        2,230,000,000
204 2005               Katrina LA,MS        3       81,000,000,000
205 2005               Ophelia    NC        1        1,600,000,000
206 2005                  Rita    TX        3       10,000,000,000
207 2005                 Wilma    FL        3       20,600,000,000
    Normalized.PL05 Normalized.CL05  X X.1
202     320,000,000     320,000,000 NA  NA
203   2,230,000,000   2,230,000,000 NA  NA
204  81,000,000,000  81,000,000,000 NA  NA
205   1,600,000,000   1,600,000,000 NA  NA
206  10,000,000,000  10,000,000,000 NA  NA
207  20,600,000,000  20,600,000,000 NA  NA

要获取我们可以使用的格式的数据，考虑以下函数，

> stupidcomma = function(x){
+ x=as.character(x)
+ for(i in 1:10){x=sub(",","",as.character(x))}
+ return(as.numeric(x))}

然后将这些值转换为数字，

> base=db[,1:4]
> base$Base.Economic.Damage=Vectorize(stupidcomma)(db$Base.Economic.Damage)
> base$Normalized.PL05=Vectorize(stupidcomma)(db$Normalized.PL05)
> base$Normalized.CL05=Vectorize(stupidcomma)(db$Normalized.CL05)

从现在开始，这是我们将使用的数据集，

> tail(base)
    Year Hurricane.Description State Category Base.Economic.Damage
202 2005                 Cindy    LA        1             3.20e+08
203 2005                Dennis    FL        3             2.23e+09
204 2005               Katrina LA,MS        3             8.10e+10
205 2005               Ophelia    NC        1             1.60e+09
206 2005                  Rita    TX        3             1.00e+10
207 2005                 Wilma    FL        3             2.06e+10
    Normalized.PL05 Normalized.CL05
202        3.20e+08        3.20e+08
203        2.23e+09        2.23e+09
204        8.10e+10        8.10e+10
205        1.60e+09        1.60e+09
206        1.00e+10        1.00e+10
207        2.06e+10        2.06e+10

数据探索

我们可以直观地看到1900年至2005年的207次飓风的成本（这里的x轴不是时间，它只是损失的指数）

> plot(base$Normalized.PL05/1e9,type="h",ylim=c(0,155))

 

通常，计算保险合同的纯保费时有两个部分。索赔数量（或此处的飓风）以及每项索赔的个人损失。我们已经看到了个人损失，现在让我们集中讨论年度频率。

> db[88:93,]
   years counts
88  2003      3
89  2004      6
90  2005      6
91  1902      0
92  1905      0
93  1907      0

平均而言，我们每年大约遭受2次（主要）飓风，

> mean(db$counts)
[1] 1.95283

广义线性模型预测

在预测模型中（此处，我们希望为2014年的再保险合同定价），我们可能需要考虑飓风发生频率的某些可能趋势。我们可以考虑用glm预测线性趋势或指数趋势

我们可以绘制这三个预测，并预测2014年（主要）飓风的数量，

constant   linear exponential
126  1.95283 3.573999    4.379822
> points(rep((1890:2030)[126],3),prediction,col=c("black","red","blue"),pch=19)

 

观察到改变模型将改变纯粹的溢价：如果预测不变，我们预计飓风将少于2（主要），但是随着指数趋势的发展，我们预计将超过4。

这是预期的频率。现在，我们应该找到一个合适的模型来计算再保险条约的纯保费，并具有（高）免赔额和有限（但大）赔付额。合适的模型是一个帕累托分布（见Hagstrœm（1925年）。

估计帕累托分布尾部指数

 

显然，主要飓风造成的损失惨重。

现在，考虑一家拥有5％市场份额的保险公司。我们将考虑\ tilde Y_i = Y_i / 20。损失如下。考虑一个再保险条约，其免赔额为2（十亿），有限承保范围为4（十亿），

 

对于我们的帕累托模型，仅考虑5亿美元以上的损失，

xi      beta 
0.4424669 0.6705315

八分之一的飓风达到了该水平

[1] 0.1256039

计算再保险合同的预期价值

鉴于损失超过5亿，我们现在可以计算再保险合同的预期价值，

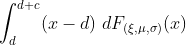
 现在，我们预计每年的飓风会少于2（主要）

> predictions[1]
[1] 1.95283

每个飓风给我们的保险公司带来超过5亿的损失的机率是12.5％，

> mean(base$Normalized.PL05/1e9/20>.5)
[1] 0.1256039

并假设飓风造成的损失超过5亿美元，那么再保险公司的预期还款额（百万）

> E(2,6,gpd.PL[1],gpd.PL[2])*1e3
[1] 330.9865

所以再保险合同的纯保费就是

[1] 81.18538

覆盖40亿，超过2个。