列举一些中位数和众数的常见问题和解法
1. 众数
一个长度为$N$的列表,出现次数大于$\left \lfloor N/2 \right \rfloor$的数为这个列表的众数。
1.1 摩尔投票算法
摩尔投票算法(Boyer-Moore majority vote algorithm)的思路类似一个大乱斗,遇到不相同的数就抵消掉。维护两个变量:major和count,major是众数的可能值,count是这个数的得分,初值都是0,顺序遍历整个列表,通过下面的条件修改major和count。
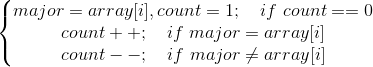
如果众数存在,程序结束的时候major就是众数。从算法里面可以看出,不想等的数之间是存在竞争关系的,相等的数则没有。我们将一个列表(例如$[1,2,1,2,1,3,1]$)分成两个组,众数一组($[1,1,1,1]$),其他的数是一组($[2,2,3]$),那众数这一组由于数值一样,只和另一组数存在竞争关系,而另一组数不仅和众数这一组有竞争关系,组内也会由于数值不等存在竞争关系,最终一定不会在乱斗中存活下来,所以如果众数存在,最终的major只可能是众数。但是要注意,这是在众数存在的情况下,如果众数不一定存在,则还需要对算法筛选出来的结果进行计数验证。算法模版如下,时间复杂度$O(n)$,空间复杂度$O(1)$。
1 def Moore(nums: List) -> int:
2 major, count = 0, 0
3 for num in nums:
4 if count == 0:
5 major, count = num, 1
6 elif major != num:
7 count -= 1
8 else:
9 count += 1
10 # 如果没有说众数一定存在,此处就要加上验证
11 return major摩尔选举方法也可以进行拓展,用来求序列中出现次数大于$\left \lfloor N/K \right \rfloor$的数。以$K=3$举例,当出现3个互不相等的数时就抵消,最后剩下的数(不会超过$K-1$个)再进行验证就可以得到最终的结果。具体的代码见$1.4$。
1.2 随机选举
随机选举的方式比较有意思,可以用来求数据流中任意区间的众数。在知道众数一定存在的情况下,单次查询时间复杂度为$O(logn)$,此外记录下标需要$O(n)$的辅助空间。简单说一下流程:首先通过字典记录每个数的下标,例如$[1,2,1,3,1]$,记录下标的字典为$\{1:[0,2,4], 2:[1], 3:[3]\}$。给定区间$[l, r]$,每次在这个区间上随机选择一个数,在字典中以这个数为key的键值列表中通过二分找到$lower\_bound(l)$和$upper\_bound(r)$,相减就是这个数在区间$[l,r]$中出现的的次数了。如果众数存在,由几何分布可知6次随机选择选到众数的概率超过$99\%$,但是如果众数不存在就会一直随机选举,如果程序允许小概率的误差,也可以在选举一定次数后就退出告知众数不存在。相关的代码见$1.4$。
1.3 转换成求中位数
如果众数存在,那么众数一定和中位数相等,那我们就可以用中位数的算法了。这里问题仍可简化,只需要求第$\left \lceil N/2 \right \rceil$大的数即可。求数组第K大的数的算法见中位数的求法,当众数不一定存在时,结果需要进行验证。这种方法的时间复杂度为$O(n)$,空间复杂度为$O(1)$。
1.4 举例
1.4.1 求长度为N的序列中出现次数大于$\left \lfloor N/K \right \rfloor$的数
1 def MoorePro(nums: List, K: int) -> List[int]:
2 majors = {}
3 for num in nums:
4 if num in majors:
5 majors[num] += 1 # 已经存在就计数
6 elif len(majors) == K - 1:
7 minusOne(majors) # 集齐K个不等元素就消除
8 else:
9 majors[num] = 1 # 元素还不存在直接新增
10
11 # 这时字典中的key就是可能的结果了,需要进一步计数验证
12 for key in majors.keys():
13 majors[key] = 0 # 先归零
14 for num in nums:
15 if num in majors:
16 majors[num] += 1
17 threshold = len(nums) // K
18 return [key for key, value in majors.items() if value > threshold]
19
20
21 def minusOne(majors: Dict) -> NoReturn:
22 remove_list = []
23 for key, value in majors:
24 if value == 1:
25 remove_list.append(key) # 遍历的时候不能直接删除
26 else:
27 majors[key] -= 1
28 for key in remove_list:
29 majors.pop(key)时间复杂度$O(NK)$,空间复杂度为$O(K)$。Leetcode 169和Leetcode 229可以拿来练练手。
1.4.2 Leetcode 1157
我们用随机选举和摩尔选举+线段树来解题,代码如下,对线段树不了解的看<<稀疏表、树状数组和线段树>>。
1 class MajorityChecker:
2 """
3 随机选举,初始化复杂度为O(n),每次query的复杂度为O(lgn),支持向列表尾部插入数据,只需要更新相应的indices字典即可
4 """
5 def __init__(self, arr: List[int]):
6 self.arr = arr
7 self.indices = collections.defaultdict(list)
8 for index, value in enumerate(arr):
9 self.indices[value].append(index)
10
11 def query(self, left: int, right: int, threshold: int) -> int:
12 # 选择10次,失败概率为1/(2^10)
13 for _ in range(10):
14 candidate = self.arr[random.randint(left, right)]
15 if bisect.bisect_right(self.indices[candidate], right) - bisect.bisect_left(self.indices[candidate], left) >= threshold:
16 return candidate
17 return -1对于可变区间问题,我们较容易想到线段树这类数据结构,关键在于这类问题有没有区间分解特性。设输入序列为$arr$,$cur$代表当前处理的线段树节点,$start$和$end$是节点代表的区间$[start, end]$,$left$和$right$代表左右儿子节点,每个节点维护两个值:$major$是众数候选项,$count$可以理解成这个$major$对应的评分。我们先给出更新关系,再说明如果区间的众数存在,major维护的就是区间众数。
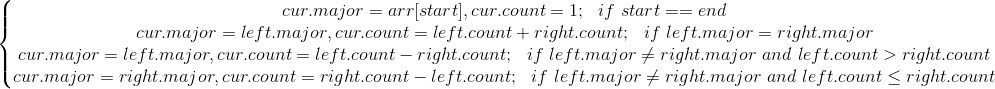
再介绍摩尔选举算法的时候,我们是顺序遍历列表进行抵消的,这里相当于先分组进行抵消,然后组之间再进行抵消,直到选出最终的胜者,有点类似体育比赛,这样如果众数存在,区间里的major就是众数。但是仍要对最终的结果进行验证。代码如下...
1 class STNode:
2 def __init__(self, major, count):
3 self.major = major
4 self.count = count
5
6
7 class MajorityChecker:
8 def __init__(self, arr: List[int]):
9 self.arr = arr
10 # 用于验证的下标字典
11 self.indices = collections.defaultdict(list)
12 for index, value in enumerate(arr):
13 self.indices[value].append(index)
14 self.STree = [STNode(0, 0) for _ in range(4 * len(arr) + 1)]
15 if self.arr:
16 self.buildSegmentTree(1, 0, len(arr) - 1)
17
18 def buildSegmentTree(self, cur: int, start: int, end: int):
19 if start == end:
20 self.STree[cur].major = self.arr[start]
21 self.STree[cur].count = 1
22 return
23 left, right, mid = cur << 1, cur << 1 | 1, start + end >> 1
24 self.buildSegmentTree(left, start, mid)
25 self.buildSegmentTree(right, mid + 1, end)
26 if self.STree[left].major == self.STree[right].major:
27 self.STree[cur].major = self.STree[left].major
28 self.STree[cur].count = self.STree[left].count + self.STree[right].count
29 elif self.STree[left].count > self.STree[right].count:
30 self.STree[cur].major = self.STree[left].major
31 self.STree[cur].count = self.STree[left].count - self.STree[right].count
32 else:
33 self.STree[cur].major = self.STree[right].major
34 self.STree[cur].count = self.STree[right].count - self.STree[left].count
35
36 def _query(self, root: int, start: int, end: int, qstart: int, qend: int) -> STNode:
37 if start == qstart and end == qend:
38 return self.STree[root]
39 left, right, mid = root << 1, root << 1 | 1, start + end >> 1
40 if qend <= mid:
41 return self._query(left, start, mid, qstart, qend)
42 elif qstart > mid:
43 return self._query(right, mid + 1, end, qstart, qend)
44 else:
45 left_res = self._query(left, start, mid, qstart, mid)
46 right_res = self._query(right, mid + 1, end, mid + 1, qend)
47 if left_res.major == right_res.major:
48 return STNode(left_res.major, left_res.count + right_res.count)
49 elif left_res.count > right_res.count:
50 return STNode(left_res.major, left_res.count - right_res.count)
51 else:
52 return STNode(right_res.major, right_res.count - left_res.count)
53
54 def query(self, start: int, end: int, threshold: int) -> int:
55 res = self._query(1, 0, len(self.arr) - 1, start, end).major
56 # 对结果进行验证
57 if bisect.bisect_right(self.indices[res], end) - bisect.bisect_left(self.indices[res], start) < threshold:
58 return -1
59 return res创建线段树的时间开销是$O(n)$,查询和验证的时间开销是$O(lgn)$,不同于随机选举,线段树的方式不支持添加元素。
2. 中位数
计算有限序列的中位数的方法是:把序列按照大小的顺序排列,如果数据的个数是奇数,则中间那个数据就是中位数,如果数据的个数是偶数,则中间那2个数的算术平均值就是中位数。只要我们可以计算数组中第K大的数,就可以得到中位数了。<<算法导论>>第9章“中位数和顺序统计量”中介绍了“期望时间为$O(n)$”和“最坏时间为$O(n)$”的两种方法,里面有对算法的详细描述和时间复杂度的严谨证明,有兴趣可以去参阅一下。“期望时间为$O(n)$”的方法平时用得较多,它参考了快速排序中的序列划分的方法,区别的地方是快速排序会递归处理划分的两边,而这里我们只需要处理一边就可以了。下面给出算法模版...
1 def findK(arr: List, start: int, end: int, K: int) -> int:
2 select = random.randint(start, end)
3 pivot, arr[select] = arr[select], arr[start]
4 l, r = start, end
5 while l < r:
6 while l < r and arr[r] > pivot:
7 r -= 1
8 if l < r:
9 arr[l] = arr[r]
10 l += 1
11 while l < r and arr[l] <= pivot:
12 l += 1
13 if l < r:
14 arr[r] = arr[l]
15 r -= 1
16 arr[l] = pivot
17 if l == K:
18 return pivot
19 elif l < K:
20 return findK(arr, l + 1, end, K)
21 else:
22 return findK(arr, start, l - 1, K)这种方法也可用来求序列种前K大的数,因为每次迭代以后pivot右边的元素都比左边的元素大。因为pivot是随机选择的,所以可以保证接近期望时间,但是有一种情况除外,当序列中元素全部相等的时候,时间复杂度为$O(n^2)$,序列中互异元素越多,时间表现越好。





















