面试高频之汉诺塔问题

普通汉诺塔

感兴趣的童鞋可以与我联系和交流~

汉诺塔（港台：河内塔）（Tower of Hanoi）是根据一个传说形成的数学问题：

有三根杆子A，B，C。A杆上有 N 个 (N>1) 穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至 C 杆：

1. 每次只能移动一个圆盘；
2. 大盘不能叠在小盘上面。

可以将圆盘临时置于 B 杆，也可将从 A 杆移出的圆盘重新移回 A 杆，但都必须遵循上述两条规则。

对于这个问题我们可以从简单的看起，然后发现规律。从规律中摸索出解决这个问题的办法。通常汉诺塔被作为学习递归的入门案例。这篇文章将吃透汉诺塔思想及其变形的题目。

我们从只有一个盘子的时候开始研究。很简单，直接把红色的盘子移到B上就可以了。

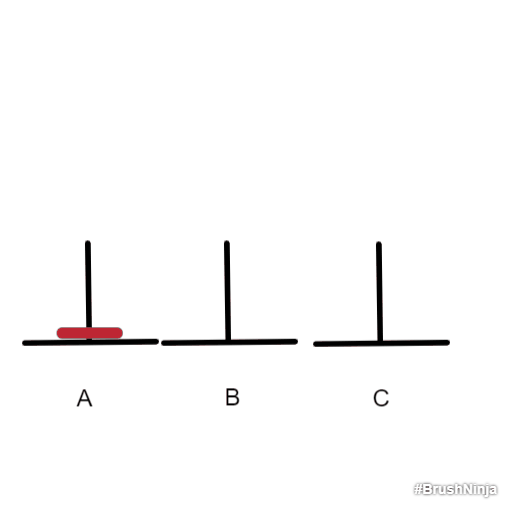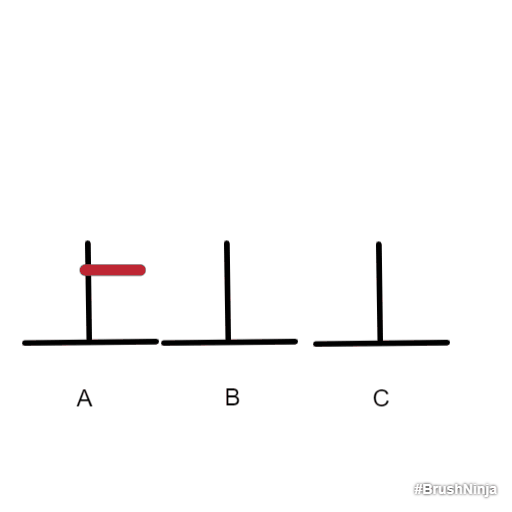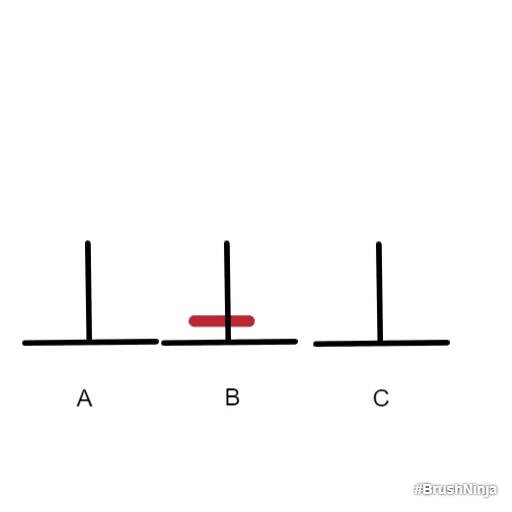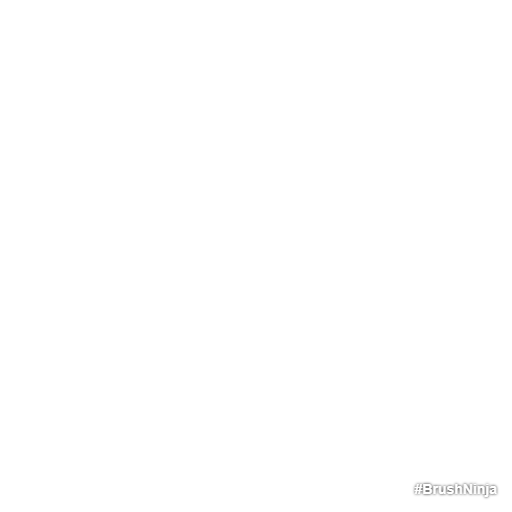
现在我们来研究两个盘子的情况：

• 我们的思路是先把最底下的大盘子放到B上，但是由于盘子大小不一样，所以我们得想办法先把上面的盘子放到C上，这样才可以把下面的大盘子放到B上，再把上面的小盘子放到B上

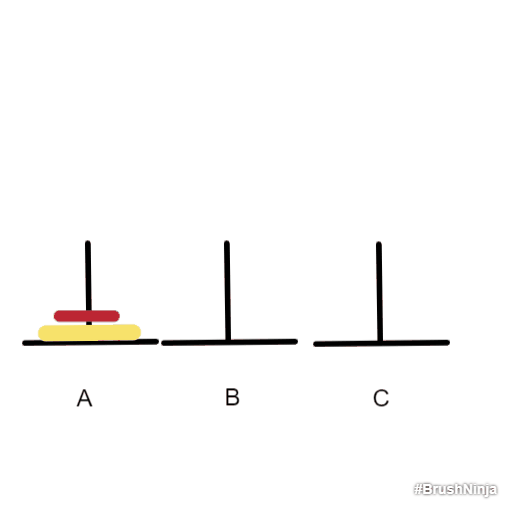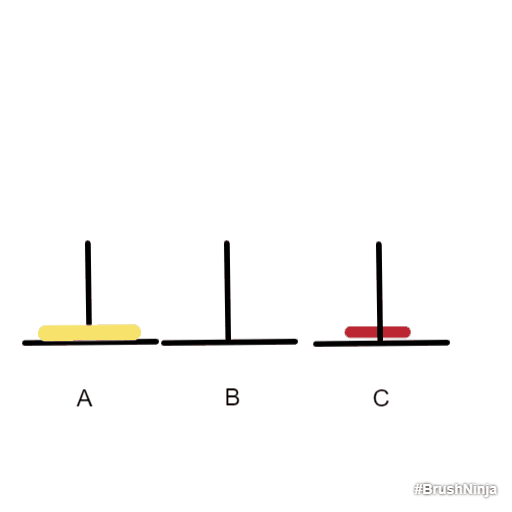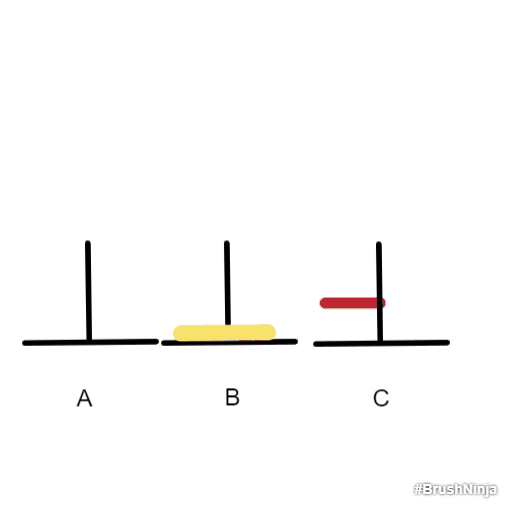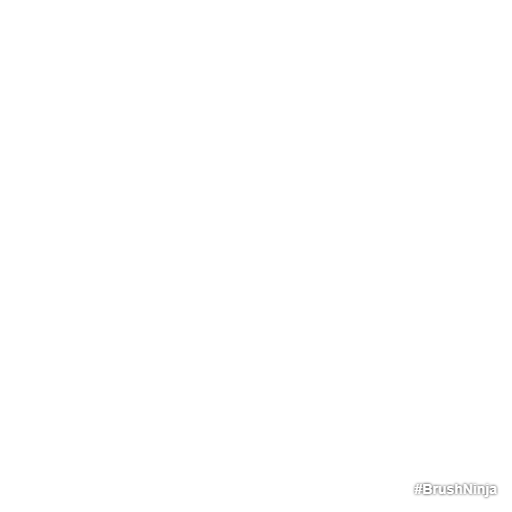
步骤：

1. 色盘子移到C上

1. 色盘子移到B上
2. 色盘子移到B上

此时两个盘子都在B上，并且红色盘子在黄色盘子上面

接下来再来看三个盘子的情况

• 要都放到B上，就必须先把蓝色上面的两个盘子想办法移到C 上，这样才能把蓝色的盘子移到B上。因此，先把红色和黄色移到C上，现在问题变成了只有两个盘子的情况，也就用到了上面的三步。然后再把蓝色盘子移到B上。最后把黄色和红色盘子移到B上，也就又回到了上面只有两个盘子的情况。

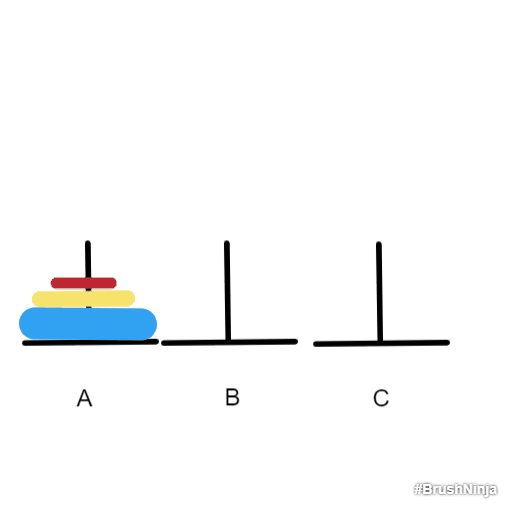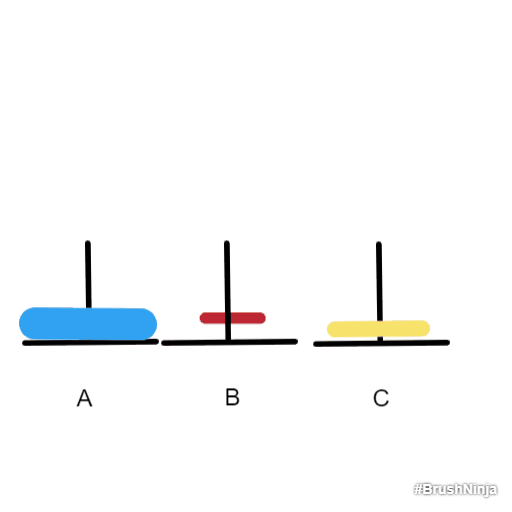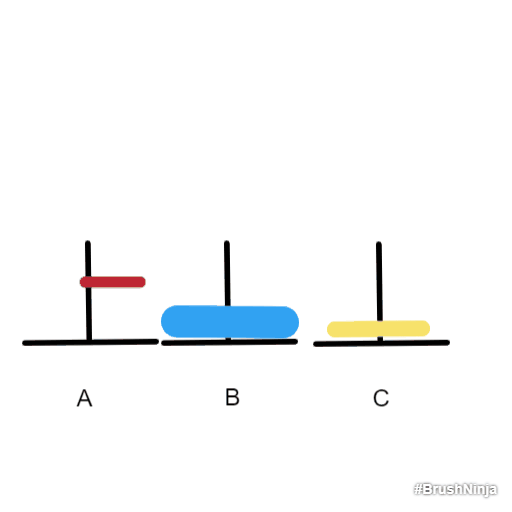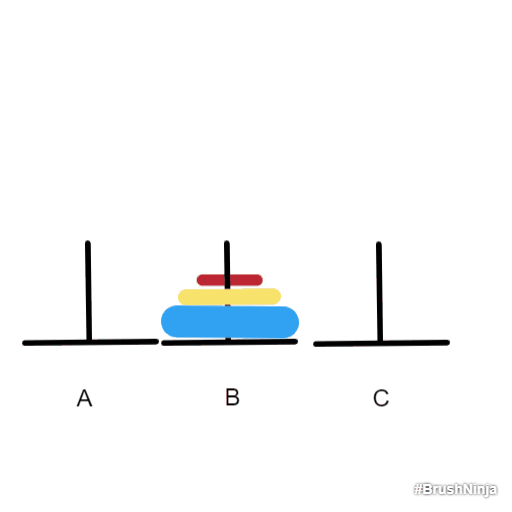
步骤：

1. 红色盘子移到B上
2. 黄色盘子移到C上
3. 红色盘子移到C上
4. 蓝色盘子移到B上
5. 红色盘子移到A上
6. 黄色盘子移到B上
7. 红色盘子移到B上

可见，完全可以把三个盘子的情况转化成两个盘子的情况，然后得以解决。

根据上面的规律可以知道：

n盘子从A移动到B = 先把 n - 1 个盘子从A移动到C + 把最底下的盘子移动到B + 最后把 n - 1个盘子从C移动到B上

即 ： 公式 H ( n ) = H ( n - 1 ) + 1 + H ( n - 1 )

数学方法适合计算移动的次数，递归法计算次数和显示移动路径均可，后同。

现在思路清楚了，我们来讲它的两种解法：

解法一(数学方法)：

//换元法+数学归纳法

H( n ) = H( n - 1 ) + 1 + H( n - 1 )
     = 2 * H( n - 1 )  +  1
//两边同时加1
H( n ) + 1 = 2 * [ H( n - 1 ) + 1 ]
//令U( n ) = H( n ) + 1
H( n ) + 1 = 2 * [ H(n - 1 ) + 1 ]
//则可变为
U( n ) = 2 * U( n - 1 )    
       = 2^2 * U( n - 2 ) = ······
       = 2^(n-1) * U(1) = 2^n
//因此解得 H( n ) = 2^n - 1

解法二（递归法）：

unsigned int count = 0;
void hanio(int n,char A,char B,char C){
    
  if(n==1)
     cout<<"Put "<<n<<" from "<<A<<" to "<<B<<endl;// 如果只有一个，那么把这个盘子直接放到B上就可以
       count += 1;
  else
  {
     hanio(n-1,A,C,B);    //借助B把前n-1个盘子从A移动到C上
     cout<<"Put "<<n<<" from "<<A<<" to "<<B<<endl; //把最下面的盘子从A移动到B上
       count += 1;
     hanio(n-1,C,B,A);   //借助A把刚才上面的n-1个盘子从C移动到B上
}

变形题1（变化条件）：

假如有2N个盘子，盘子种类有N种，并且每种盘子有两个（这两个大小和颜色完全相同）

思路点拨：以前移动1个盘子：例如红色移动到C上，现在无非就是把两个红色的移动到C上，因为这两个盘子完全一样，所以只要把原来的移动一次，现在改成移动两次就可以了

**新2n盘子从A移动到B = 2 * 之前n个盘子移动次数**

因此，依然有两种解法：

解法一(数学方法)：

//换元法+数学归纳法
//G(n)代表新的规则下的移动次数
G( n ) = 2 * H( n )
     = 2 * ( 2^n - 1 )
       = 2^(n + 1) - 2

解法二（递归法）：

unsigned int count = 0;
void hanio(int n,char A,char B,char C){
    
    if(n == 2 ){
       cout<<"Put "<<n<<" from "<<A<<" to "<<B<<endl;// 如果只有两个，那么把这两个盘子直接放到B上就可以
       cout<<"Put "<<n-1<<" from "<<A<<" to "<<B<<endl;
       count += 2;
    }
    else
    {
       hanio(n-2,A,C,B);    //借助B把前n-2个盘子从A移动到C上
       cout<<"Put "<<n - 1<<" from "<<A<<" to "<<B<<endl;   //把最下面的两个盘子从A移动到B上
       cout<<"Put "<<n<<" from "<<A<<" to "<<B<<endl;   //
       count += 2;
       hanio(n-2,C,B,A);   //借助A把刚才上面的n-2个盘子从C移动到B上
}

变形题2（变化条件）：

假如A和B直接不能直接移动，那么怎么解决？

思路点拨：既然不能直接在A和B直接移动，那么想从A移动到B，或者从B移动到A，都需要借助C来实现，先移动到C再移动到A或B

步骤：

1. 先把 n - 1 个通过C移动到B上
2. 把最底部的移动到C上
3. 再通过C把B上的n-1个移动到A上
4. 把底部的移动到B上
5. 最后把n - 1 个通过C移动到B上

移动n个盘子需要的次数 = 通过C移动n-1个盘子到B的次数 + 把最底部移动到C上的次数 + 通过C再次移动n-1个盘子到A的次数 + 把最底部盘子移动到B上次数 + 通过C把n-1个盘子移动回B的次数因此，依然有两种解法：

解法一(数学方法)：

//为了区别此处改为G(n)
G( n ) = G( n - 1 ) + 1 + G( n - 1 ) + 1 + G( n - 1 )
// 同理,此次省略数学推导过程,证明思路和第一个一样,有兴趣可以联系作者
       = 3^n - 1

解法二（递归法）：

unsigned int count = 0;
void hanio(int n,char A,char B,char C){
    
    if(n == 1 ){
       cout<<"Put "<<n<<" from "<<A<<" to "<<B<<endl;// 如果只有一个，那么把这个盘子先放到C上
       cout<<"Put "<<n<<" from "<<C<<" to "<<B<<endl;// 把这个盘子再放到B上
       count += 2;
    }
    else
    {
       hanio(n-1,A,B,C);                                 //把n-1个通过C移动到B上 
       cout<<"Put "<<n<<" from "<<A<<" to "<<C<<endl;   //把最底部的移动到C上
       count += 1;
       hanio(n-1,B,A,C);                                //再通过C把B上的n-1个移动到A上
       cout<<"Put "<<n<<" from "<<C<<" to "<<B<<endl;   //把底部的移动到B上
       count += 1;        
       hanio(n-2,A,B,C);                                 //最后把n-1个通过C移动到B上
}

欢迎关注，支持原创！