适合聚类分析回归分析关联规则的数据

聚类

一、简介

    聚类即物以类聚，他是为了实现将数据按照某一标准（相似度）将整个数据集分为若干子集（簇），最终的分类结果要尽量保证组内相似度尽可能大，组间相似度尽可能小。
    聚类是典型的无监督学习（Unsupervised learning），它与分类问题最明显的区别就是分类问题有事先的标注，而聚类的分组是完全靠自己学习得来的。
    聚类可以作为一个单独的学习过程，为了寻找数据的内部分布结构，也可以作为其他任务的前驱过程。

二、相似度度量

    上面提到聚类的分类需要按照某一标准进行分类，这一标准常常是计算两数据之间的相似度进行判断。下图是对相似度计算方式的总结：

    其中Minkowski距离是所有范式距离的统称，p=1时为曼哈顿距离，p=2时为欧式距离

三、常见的聚类方法

    聚类的方法大致可分为以下几类：
        基于划分的聚类，如K-means
        层次聚类，如Agglomerative clustering
        密度聚类，DBSCAN
        基于模型的聚类：高斯混合模型（GMM）
        谱聚类（Spectral clustering）、AP聚类算法（Affinity propagation）等。

四、聚类方法介绍

4.1 K-means

    1、算法思想
    基于划分的算法，想要的效果就是在需要聚类的散点数据集中划分出类内点足够近，类间点足够远。
    2、算法流程：
    · 随机选择K个对象，每个对象表示一个簇的初始中心
    · 对剩余的数据点，根据他到不同中心距离选择最短距离的中心点将其分类
    · 分完后重新计算每个簇的均值，更新中心点
    · 不断重复第二步和第三步，直到中心点位置变化不大为止。
    3、算法优缺点：
        优点：
        · 简单高效
        · 时空复杂度都较低
        缺点：
        · 需要预先设定K值且对一开始的随机点位置很敏感
        · 容易形成局部最优解
        · 对噪声和离群值很敏感
        · 不能解决非凸（non-convex）数据

4.2 DBSCAN

    1、算法思想：

    DBSCAN这类基于密度的算法更像是人眼观察的分类结果，他对于处理不规则形状的分布和噪点都有较好的效果。这个算法将数据集中的点分为核心点、边缘点和噪点（如下图），然后根据自己定义的邻域进行划分。

    这里面，ε邻域表示所有到某xi点距离小于ε的集合，核心对象指其邻域中数据点多于阈值的点，其中，相同邻域的点为密度直达（下图左p,q），通过相同邻域的点能与其他邻域的点相联系的点称为密度可达（下图右p,q）。

    2、算法流程:

    整个算法就是将所有密度可达的点分为一个簇，不断寻找密度可达的点，没有则更改对象点，再开始下一个簇。

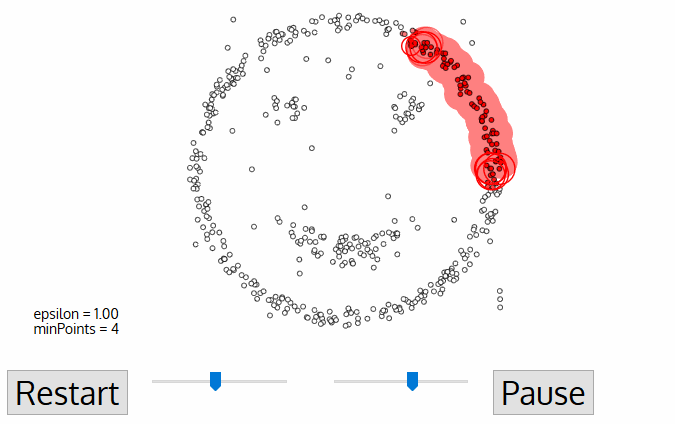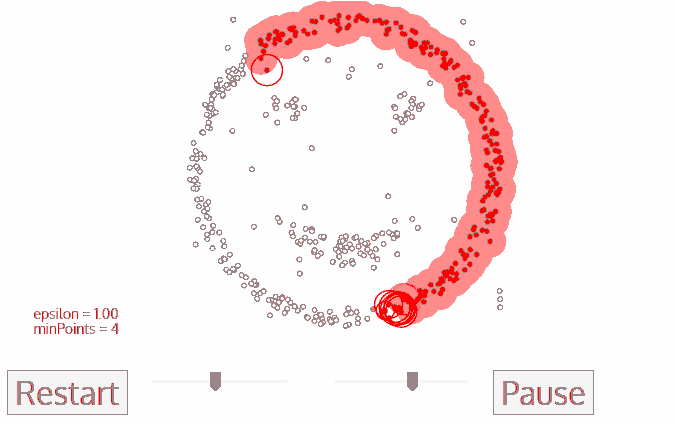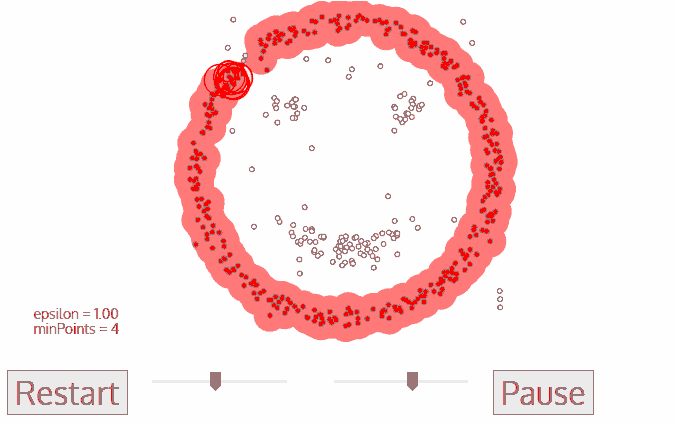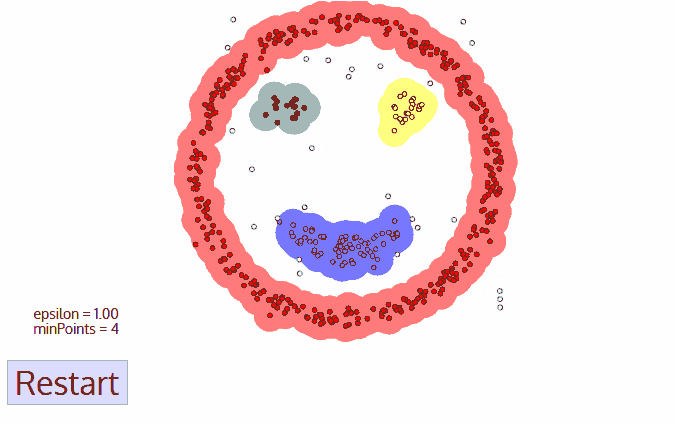
    3、算法优缺点：
        优点：
        · 对噪点不敏感
        · 能划分任意不同形状
        缺点：
        · 聚类的结果会受到初始设定的参数影响。对于稀疏程度不同的数据集，相同的判定标准会破坏聚类的结构。

4.3 高斯混合模型（GMM）

    1、高斯分布

    高斯分布有时也被称作正态分布，是满足自然规律的一种常见的数据分布情况。

    高斯分布的概率密度函数公式计算如下：

    其中μ为均值，σ表示标准差。    2、GMM

    对于高斯混合模型，计算公式可写成：

    其中N（）表示某一个分量，这个分量个数K是根据数据可以分成几个簇设定的。其中π_k可以看成加权平均的权重，且所有π_k之和为1，并且π_k大于零。

    从计算公式中可以看出，会出现K个π、μ、Σ未知数。因为在计算时是随机从图中选择分量取点，那么如何确定所取点来自哪一个簇也就是确定π值则成为一个问题。这里用到了EM（Expectation-Maximization）算法来计算参数。    3、计算过程

    说明EM计算参数之前，先利用贝叶斯思想对原式进行处理。

    通过定理中增加的参数可以看出，引入了一个隐含参数z用来描述之前提到的归属哪一个分量的问题，同时引入后验概率用于计算π、μ、Σ。

    EM算法大致分两步，第一步先计算需求参数的粗略值，第二步使用第一步的值最大化似然函数。

    EM算法：

        1、根据数据定义分量数K，然后计算$p\left( x| \pi ,\mu ,\Sigma \right) =\sum ^{k}_{k=1}\pi _{k}N\left( x| \mu _{k},\Sigma _{k}\right)$的对数似然函数。

        2、根据当前的π_k、μ_k、Σ_k计算后验概率。

        3、根据第2步计算得到的后验概率计算新的π_k、μ_k、Σ_k

    其中:$N_{k}={\sum ^{N}_{n=1}γ(z_{nk})}$

        4、检查参数是否收敛或对数似然函数是否收敛，若不收敛，则返回第2步。

    4、GMM相较于K-means的优势

        1、灵活。根据标准差参数，GMM可以采用任意椭圆形状而不是单一的圆形。K-means实际是GMM的一个特例。

        2、由于GMM提供的不是一个硬性的聚类，而是一个概率，每个数据点可以有多个聚类。所以对于处于两个簇交叉区域的点可以给两个概率分别表示它属于某一个类的概率。

4.4层次聚类

    层次聚类可以分成自上而下或自下而上两种，自下而上是先将每个样本视为自己一类，然后进行依次向上聚合，又称为凝聚，自上而下则是先视为一类，在进行细分。

    下图展示了自下而上的聚类动态过程，便于理解。

    层次聚类不需要指定聚类的数量，并且对距离度量的选择不敏感。但效率很低，时间复杂度为O(n³)。