python 道格拉斯普克 道格拉斯理论

        道格拉斯-普克算法（Douglas–Peucker algorithm），亦称为拉默-道格拉斯-普克算法（Ramer–Douglas–Peucker algorithm），这个算法最初由拉默（Urs Ramer）于1972年提出，1973年道格拉斯（David Douglas）和普克（Thomas Peucker）二人又独立于拉默提出了该算法。

        在计算机当中，曲线可以用足够多的点来描述，那么如何用尽可能少的点来描述这条曲线呢，这就是该算法要实现的目标，同时因为用来描述曲线的点变少了，也可以认为其对数据进行了压缩，减少了数据量。

算法作用 

        如何存储一条曲/折线？常见的方式就是使用使用一系列坐标点的集合来表示，点越多越密集，那么所能表示的精度就越高。在GIS画图的时候理想状况下，我们当然希望精度越高越好，但高精度的数据也会带来一些问题，比如对硬件系统的要求变高；比如在一些可视化场景里造成的渲染问题。

        道格拉斯-普克算法正是用来解决这些问题的，它可以在保证一定精度的前提下，简化曲线的绘制过程，也是目前被广泛应用的GIS算法。基于线状实体的点压缩算法，用来压缩简化矢量数据。

算法流程

1. 输入一系列坐标点组成的曲线。
2. 曲线第一个点A和最后一个点B连成一条直线AB。
3. 确认一个阈值（这个值用于控制简化后曲线的精度）
4. 分别计算曲线上各点到这条直线的距离，并取出其中的最远距离与阈值进行比较。
5. 如果最远距离大于阈值，则将该点保留，记为C，此时可以生成两条直线AC、CB，重复步骤4
6. 否则将该点舍弃。

这么描述的有点抽象，我们还是看百科里给的动图。

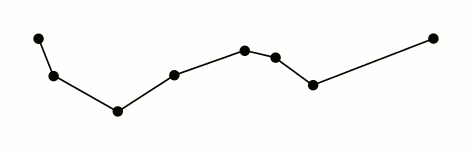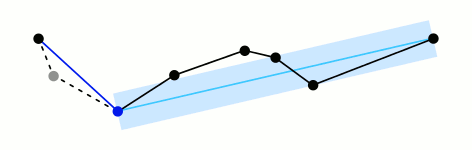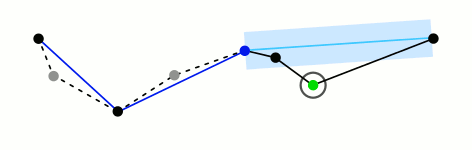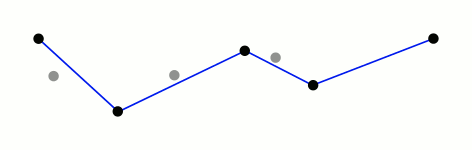
图解 

 

 

 代码实现

# -*- coding:utf-8 -*-
"""
道格拉斯算法的实现
程序需要安装shapely模块
"""
import math
from shapely import wkt, geometry
import matplotlib.pyplot as plt


class Point:
    """点类"""
    x = 0.0
    y = 0.0
    index = 0  # 点在线上的索引

    def __init__(self, x, y, index):
        self.x = x
        self.y = y
        self.index = index


class Douglas:
    """道格拉斯算法类"""
    points = []
    D = 1  # 容差

    def readPoint(self):
        """生成点要素"""
        g = wkt.loads("LINESTRING(1 4,2 3,4 2,6 6,7 7,8 6,9 5,10 10)")
        coords = g.coords
        for i in range(len(coords)):
            self.points.append(Point(coords[i][0], coords[i][1], i))

    def compress(self, p1, p2):
        """具体的抽稀算法"""
        swichvalue = False
        # 一般式直线方程系数 A*x+B*y+C=0,利用点斜式,分母可以省略约区
        # A=(p1.y-p2.y)/math.sqrt(math.pow(p1.y-p2.y,2)+math.pow(p1.x-p2.x,2))
        A = (p1.y - p2.y)
        # B=(p2.x-p1.x)/math.sqrt(math.pow(p1.y-p2.y,2)+math.pow(p1.x-p2.x,2))
        B = (p2.x - p1.x)
        # C=(p1.x*p2.y-p2.x*p1.y)/math.sqrt(math.pow(p1.y-p2.y,2)+math.pow(p1.x-p2.x,2))
        C = (p1.x * p2.y - p2.x * p1.y)

        m = self.points.index(p1)
        n = self.points.index(p2)
        distance = []
        middle = None

        if (n == m + 1):
            return
        # 计算中间点到直线的距离
        for i in range(m + 1, n):
            d = abs(A * self.points[i].x + B * self.points[i].y + C) / math.sqrt(math.pow(A, 2) + math.pow(B, 2))
            distance.append(d)

        dmax = max(distance)

        if dmax > self.D:
            swichvalue = True
        else:
            swichvalue = False

        if (not swichvalue):
            for i in range(m + 1, n):
                del self.points[i]
        else:
            for i in range(m + 1, n):
                if (abs(A * self.points[i].x + B * self.points[i].y + C) / math.sqrt(
                        math.pow(A, 2) + math.pow(B, 2)) == dmax):
                    middle = self.points[i]
            self.compress(p1, middle)
            self.compress(middle, p2)

    def printPoint(self):
        """打印数据点"""
        for p in self.points:
            print("%d,%f,%f" % (p.index, p.x, p.y))


def main():
    """测试"""
    # p=Point(20,20,1)
    # print '%d,%d,%d'%(p.x,p.x,p.index)

    d = Douglas()
    d.readPoint()
    # d.printPoint()
    # 结果图形的绘制，抽稀之前绘制
    fig = plt.figure()
    a1 = fig.add_subplot(121)
    dx = []
    dy = []
    for i in range(len(d.points)):
        dx.append(d.points[i].x)
        dy.append(d.points[i].y)
    a1.plot(dx, dy, color='g', linestyle='-', marker='+')

    d.compress(d.points[0], d.points[len(d.points) - 1])

    # 抽稀之后绘制
    dx1 = []
    dy1 = []
    a2 = fig.add_subplot(122)
    for p in d.points:
        dx1.append(p.x)
        dy1.append(p.y)
    a2.plot(dx1, dy1, color='r', linestyle='-', marker='+')

    # print "========================\n"
    # d.printPoint()

    plt.show()


if __name__ == '__main__':
    main()