本篇博客导图

简介&我的理解
R-B Tree 红黑树简介-3个特性
红黑树是二叉查找树的一种,与AVL平衡二叉树相差不大,也是左小右大的数据存储结构,重点在于查找数据,同样是O(height)的时间复杂度。
相对于AVL树的靠高度平衡,红黑树是靠颜色平衡的,而为了维持接下来的几个特性,使得它在插入或者删除操作以后必须进行旋转和重新着色才可以保持红黑树特质.
它主要有以下几种特性(虽然太过形式化,我很不愿意讲)
- 只包含红色和黑色两种节点
- 根节点必须是黑色
- 每个叶子节点(即null节点),我们认为是黑色
以上基本上就是红黑树的基本3个特性了,还有两个,接下来分开讲
特性4和特性5

- 特性4:红色节点的相邻节点只能是黑色节点
- 特性5:从任何一个节点出发,到它的子NULL节点,路径上的黑色节点数量是相同的。
如上图:
对于特性4我想大家都可以理解。
特性5则举例说明: 从100出发,到它子节点任何一个NULL,无论走哪一条路,都只能经过一个黑色节点.
插入
着色
值得一提的是:插入的节点默认染色都是红色的,ROOT除外,想象一下,我们每次插入都是红色的,那么肯定就会有违背特性4的时候,也就是红色节点不能相邻,这个时候就需要旋转和重新着色以达到红黑树的效果,调整之前,主要有两种情况

插入70,调整前情况
- 情况一:自身70是红色,父节点60是红色,且叔叔节点40是红色,不旋转,调整以后为红黑黑
- 情况二:自身是红色,父节点是红色,叔叔节点不存在,或为黑色,需要旋转,但我们先不关注,调整以后为黑红红(情况二我们不再给图,直接看下文)
情况一:红黑黑感知
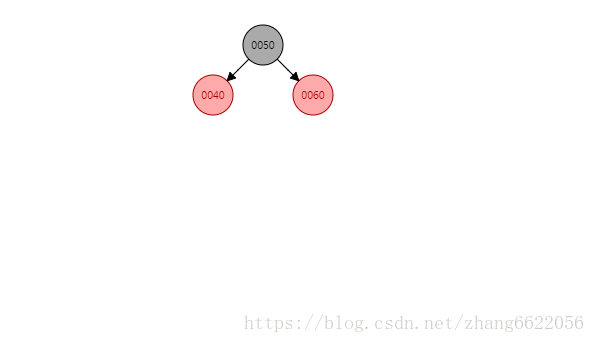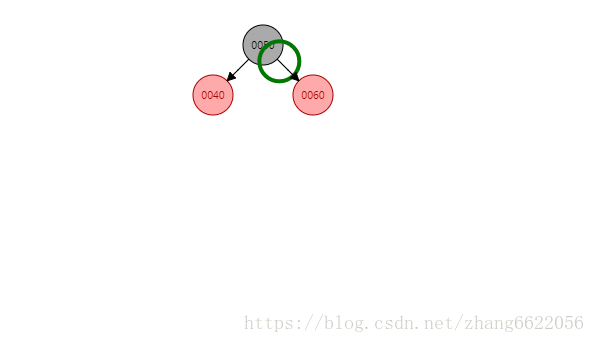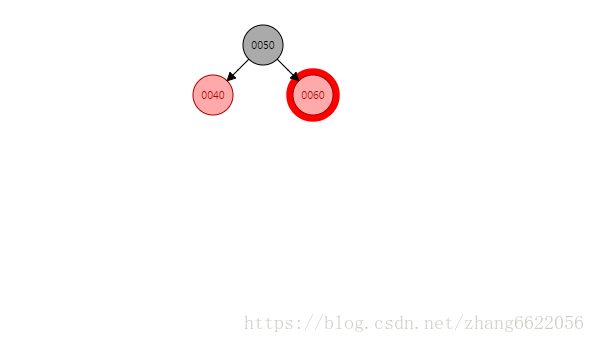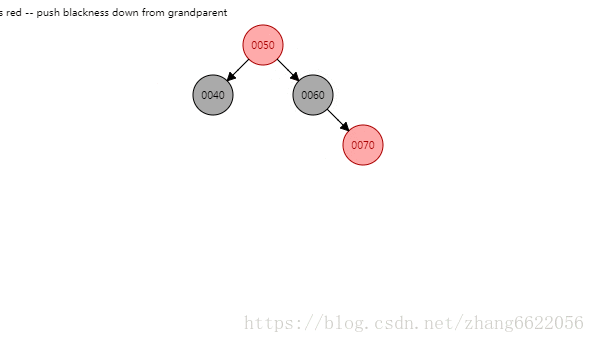
情况一:有红叔叔!!!插入完成之后着色成为了红黑黑
黑红红情况感知
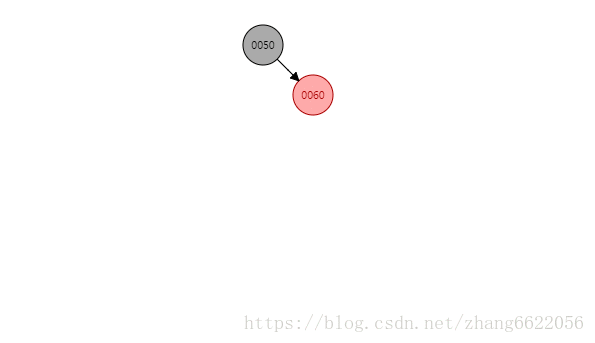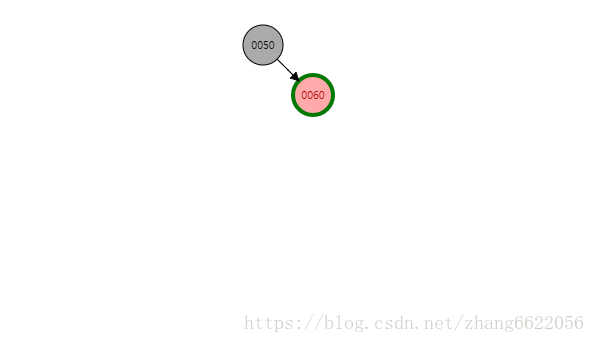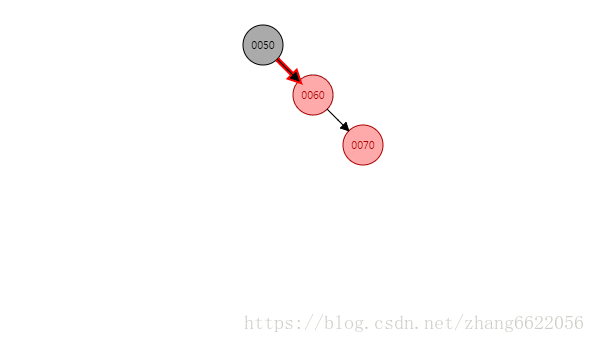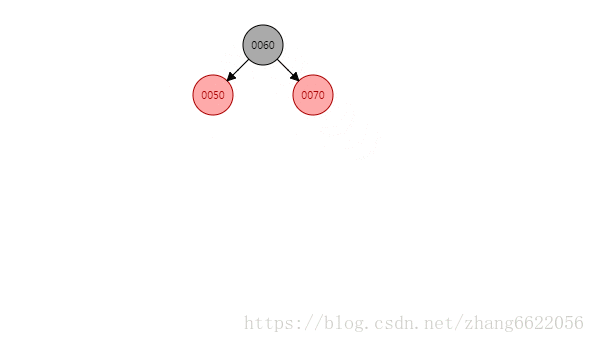
情况二:没红叔叔!!!插入完成之后着色成为了黑红红
总结:
插入操作着色并没有多难,只有以上两种情况,拆分开理解更加简单
- 插入节点:单纯的节点关联
- 插入以后默认染色为红色!!!!
- 插入以后判定是情况一还是情况二,按照上图进行处理即可
- 红黑黑:红色父节点,左右儿子都是黑色子节点
- 黑红红:黑色父节点,左右儿子都是红色子节点
旋转
左旋
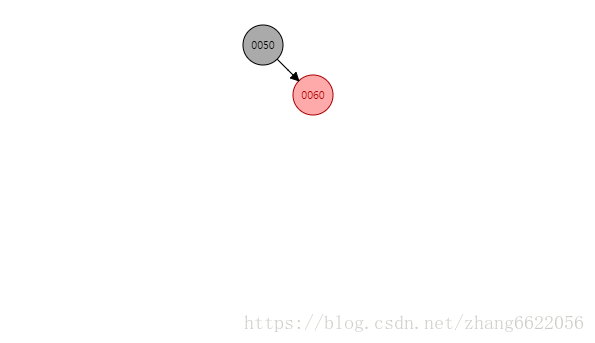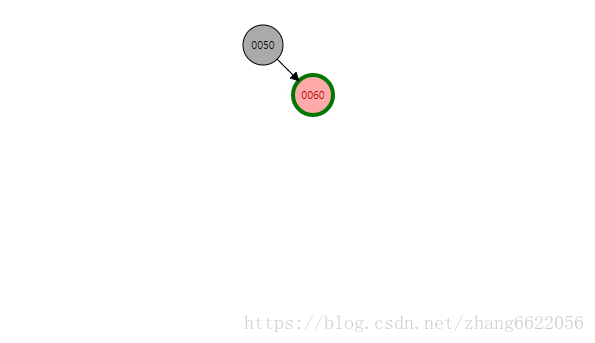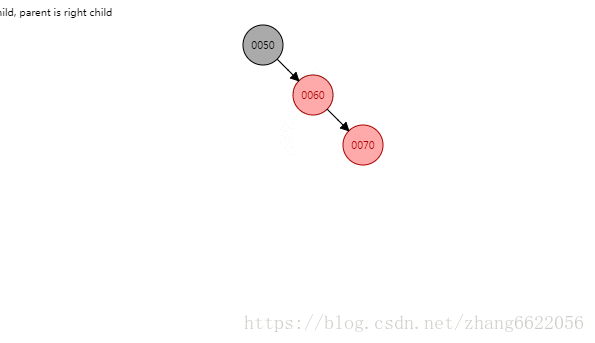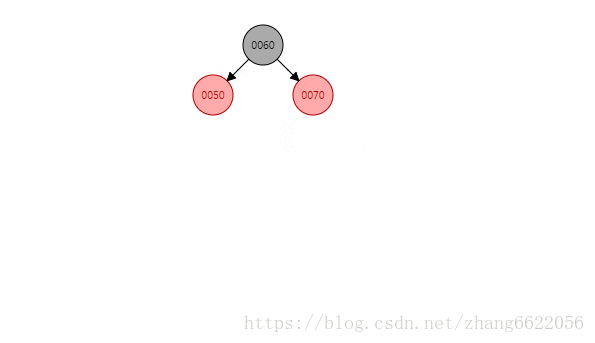
感知左旋
如上:插入,左旋,着色
- 插入操作:插入节点,进行节点关联。 60.right = 70. 70.parent = 60
- 触发旋转条件:70和60的红色相连接,违背特性4,触发旋转逻辑
- 旋转操作:旋转关键点在于找到变爸爸的那个节点,上图中为60,值得注意的地方是隐形节点关联和类双向链表关系关联。
- 由于对于70节点来讲,没有红色叔叔节点,那么此例着色为黑红红
右旋
感知右旋,不再描述,请根据上层理解
左右类型
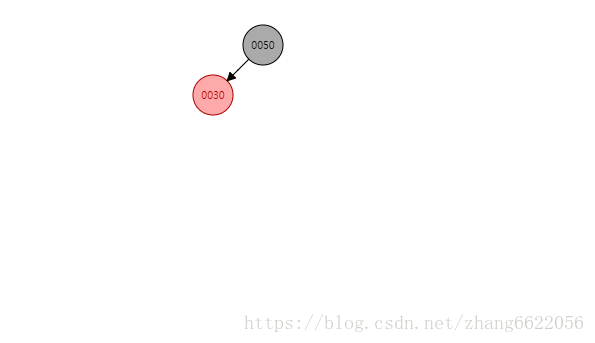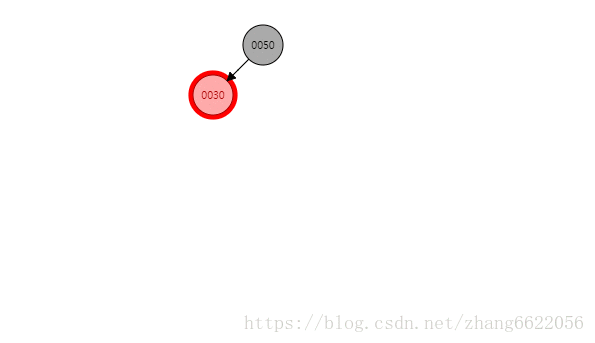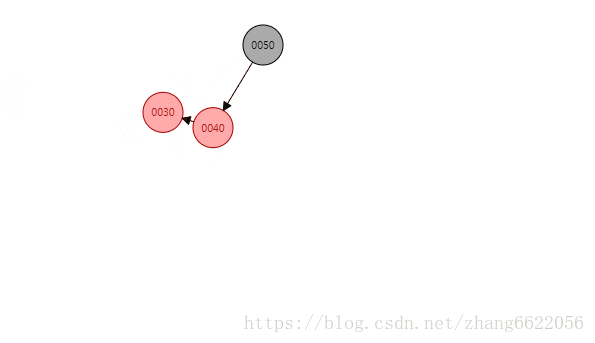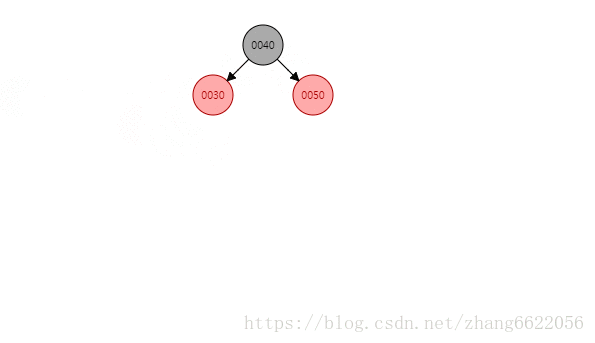
先左旋,再右旋,关键是旋转的那个点!
关键是找到从儿子变成爸爸的那个节点,此处是一样的意思,只是多了一步旋转
- 40进行左旋,从儿子变成爸爸,这时就变成了左左模型 50.left = 40.left = 30
- 40进行右旋,再次从儿子变成爸爸,完成旋转!
- 右左类型不再描述,都一样的。
插入流程总结
- 按照二叉查找数规则插入
- 判定是否红色相邻,是情况一还是情况二
- 情况一,有红色叔叔,重新重色,红黑黑
- 情况二,无红色叔叔,先旋转,再重新着色,黑红红
删除
将红黑树中的某个节点删除,其实和平衡二叉树的删除大同小异,分为以下几点

- 删除节点有两个儿子,处理方式是,找到替代节点顶替,然后删除替代节点,寻找替代节点的方式为左边最大或右边最小(如:删除49,则48着色为黑色,替换49.转换思路为删除48)
- 删除节点有一个儿子的情况,直接将删除节点的儿子作为替换节点,并着色成为删除节点颜色,替换即可(如删除46,则把45着色为黑色,替换46即可)
- 删除节点一个儿子都没有,并且删除的节点为红色,直接干掉。(如删除56,没有任何影响)
- 删除节点一个儿子都没有,并且删除的节点为黑色(最复杂!后面讨论)
删除单个黑色节点
当删除单个黑色节点的时候,这意味着红黑树的特性5肯定会被违背,因为凭空一个合格的红黑树被抽掉了一个黑色节点,这个时候,我们必须从通过旋转和重新着色的策略使它重新成为一颗红黑树,情况细分和处理方式较为复杂,分为以下几种
情况总结 | 处理方式 |
情况一:兄弟节点在右边,红色 | -兄弟节点着黑色 -父亲节点着红色 -左旋兄弟节点 -左旋后赋值新兄弟节点 |
情况二:兄弟节点在右边,黑色,且兄弟两个子节点都为黑色 | -兄弟节点着红色 -重置节点为父亲节点,继续查找 |
情况三:兄弟节点在右边,黑色,且兄弟节点左孩子红色,右孩子黑色 | -兄弟节点左孩子着黑色 -兄弟节点着红色 -右旋兄弟节点左孩子 -重新赋值兄弟节点 |
情况四:兄弟节点在右边,黑色,且兄弟节点右孩子为红色 | -兄弟节点着色父亲节点颜色 -父亲节点着黑色 -兄弟右节点着黑色 -左旋兄弟节点 赋值当前节点为root |
以上全部是删除节点在左,兄弟节点在右的情况,反过来是一样的,只不过旋转的方向需要跟着变动
代码解析
基础Node信息
public static class Node{
public static final String RED = "red";
public static final String BLACK = "black";
public int value;
public String color; //方便理解,我们就用string
public Node left;
public Node right;
public Node parent;
public Node(int value) {
this.value = value;
initNode(value,Node.RED,null,null,parent);
}
public Node(int value, String color, Node left, Node right,Node parent) {
initNode(value,color,left,right,parent);
}
private void initNode(int value, String color, Node left, Node right,Node parent){
this.value = value;
this.color = color;
this.left = left;
this.right = right;
}
//获取父亲节点
public Node getFather(){
return this.parent;
}
//获取爸爸的兄弟节点
public Node getUncle(){
if(null == this.parent) return null;
if(null == this.parent.parent) return null;
if (this.parent == this.parent.parent.left){
return this.parent.parent.right;
}else{
return this.parent.parent.left;
}
}
/***
* 获取爷爷节点
* @return
*/
public Node getGrandFather(){
if(null == this.parent) return null;
return this.parent.parent;
}
/***
* 获取兄弟节点
* @return
*/
public Node getBro(){
if(null == this.parent) return null;
if(value == this.parent.left.value){
return this.parent.right;
}else{
return this.parent.left;
}
}
}
public static class Node{
public static final String RED = "red";
public static final String BLACK = "black";
public int value;
public String color; //方便理解,我们就用string
public Node left;
public Node right;
public Node parent;
public Node(int value) {
this.value = value;
initNode(value,Node.RED,null,null,parent);
}
public Node(int value, String color, Node left, Node right,Node parent) {
initNode(value,color,left,right,parent);
}
private void initNode(int value, String color, Node left, Node right,Node parent){
this.value = value;
this.color = color;
this.left = left;
this.right = right;
}
//获取父亲节点
public Node getFather(){
return this.parent;
}
//获取爸爸的兄弟节点
public Node getUncle(){
if(null == this.parent) return null;
if(null == this.parent.parent) return null;
if (this.parent == this.parent.parent.left){
return this.parent.parent.right;
}else{
return this.parent.parent.left;
}
}
/***
* 获取爷爷节点
* @return
*/
public Node getGrandFather(){
if(null == this.parent) return null;
return this.parent.parent;
}
/***
* 获取兄弟节点
* @return
*/
public Node getBro(){
if(null == this.parent) return null;
if(value == this.parent.left.value){
return this.parent.right;
}else{
return this.parent.left;
}
}
}
- parent向上,left,right向下。类似双向链表,操作时一定要注意对应关系
- 相关角色可以不定义到内部,这里为了操作方便,但是空间复杂度会提高
左旋和右旋
/****
* 左旋
* 右右类型传入父亲节点
* 左右类型传入儿子节点
* @param currentNode 传入的永远是要变成爸爸的儿子,
* @Return node 返回最新的爸爸
*/
private Node leftRotate(Node currentNode){
//获取旋转前角色
Node grandFather = currentNode.getGrandFather();
Node father = currentNode.getFather();
//双方丢失的节点重新绑定
father.right = currentNode.left;
//绑定爷爷和父亲的角色
if(null != grandFather){ //到root节点,则重新赋值root
if(father == grandFather.left){
grandFather.left = currentNode;
}else{
grandFather.right = currentNode;
}
currentNode.parent = grandFather;
}else{
root = currentNode;
currentNode.parent = null;
}
//儿子与父节点的关联
currentNode.left = father;
father.parent = currentNode;
return currentNode;
}
/***
* 右旋
* 右右类型传入父亲节点
* 左右类型传入儿子节点
* @param currentNode 传入的永远是要变成爸爸的儿子
* @Return node 返回最新的爸爸
*/
private Node rightRotate(Node currentNode){
//获取旋转前角色
Node grandFather = currentNode.getGrandFather();
Node father = currentNode.getFather();
//双方丢失的节点重新绑定
father.left = currentNode.right;
//绑定爷爷和父亲的角色
if(null != grandFather){
if(father == grandFather.left){
grandFather.left = currentNode;
}else{
grandFather.right = currentNode;
}
currentNode.parent = grandFather;
}else{ //替换root节点
this.root = currentNode;
currentNode.parent = null;
}
//儿子与父节点的关联
currentNode.right = father;
father.parent = currentNode;
return currentNode;
}
/****
* 左旋
* 右右类型传入父亲节点
* 左右类型传入儿子节点
* @param currentNode 传入的永远是要变成爸爸的儿子,
* @Return node 返回最新的爸爸
*/
private Node leftRotate(Node currentNode){
//获取旋转前角色
Node grandFather = currentNode.getGrandFather();
Node father = currentNode.getFather();
//双方丢失的节点重新绑定
father.right = currentNode.left;
//绑定爷爷和父亲的角色
if(null != grandFather){ //到root节点,则重新赋值root
if(father == grandFather.left){
grandFather.left = currentNode;
}else{
grandFather.right = currentNode;
}
currentNode.parent = grandFather;
}else{
root = currentNode;
currentNode.parent = null;
}
//儿子与父节点的关联
currentNode.left = father;
father.parent = currentNode;
return currentNode;
}
/***
* 右旋
* 右右类型传入父亲节点
* 左右类型传入儿子节点
* @param currentNode 传入的永远是要变成爸爸的儿子
* @Return node 返回最新的爸爸
*/
private Node rightRotate(Node currentNode){
//获取旋转前角色
Node grandFather = currentNode.getGrandFather();
Node father = currentNode.getFather();
//双方丢失的节点重新绑定
father.left = currentNode.right;
//绑定爷爷和父亲的角色
if(null != grandFather){
if(father == grandFather.left){
grandFather.left = currentNode;
}else{
grandFather.right = currentNode;
}
currentNode.parent = grandFather;
}else{ //替换root节点
this.root = currentNode;
currentNode.parent = null;
}
//儿子与父节点的关联
currentNode.right = father;
father.parent = currentNode;
return currentNode;
}红黑黑和黑红红
/****
* 红黑黑类型
* @param colorNode 传入固定时间的父亲节点
*/
private void redBlackBlack(Node colorNode){
setRed(colorNode);
setBlack(colorNode.left);
setBlack(colorNode.right);
}
/*****
* 黑红红类型
* @param colorNode 传入固定时间的父亲节点
*/
private void blackRedRed(Node colorNode){
setBlack(colorNode);
setRed(colorNode.left);
setRed(colorNode.right);
}
/****
* 红黑黑类型
* @param colorNode 传入固定时间的父亲节点
*/
private void redBlackBlack(Node colorNode){
setRed(colorNode);
setBlack(colorNode.left);
setBlack(colorNode.right);
}
/*****
* 黑红红类型
* @param colorNode 传入固定时间的父亲节点
*/
private void blackRedRed(Node colorNode){
setBlack(colorNode);
setRed(colorNode.left);
setRed(colorNode.right);
}插入操作
/***
* 只有插入操作,只执行插入
* @param value 插入的值
* @return 插入完成后返回插入节点
*/
private Node doInsert(int value){
Node insertNode = new Node(value);
Node father = root;
Node tempFather = null;
while(father != null){
tempFather = father;
if(value < father.value){
father = father.left;
}else{
father = father.right;
}
}
if(value < tempFather.value){
tempFather.left = insertNode;
}else{
tempFather.right = insertNode;
}
insertNode.parent = tempFather;
return insertNode;
}
/***
* 对外开放insert
* @param value
* @throws Exception
*/
public void insert(Integer value) throws Exception {
//验证root初始化
if(null == root){
Node node = new Node(value);
setBlack(node);
this.root = node;
return;
}
//验证是否已插入节点
if(null != findValue(root,value)){
throw new Exception("不允许重复插入值");
}
Node insertNode = doInsert(value);
rebuildInsertCore(insertNode);
}
/****
* 插入之后重新构建红黑树
* @param insertNode
*/
private void rebuildInsertCore(Node insertNode){
while(null != insertNode.getFather() && insertNode.getFather().color == Node.RED && insertNode.color == Node.RED){
if(null != insertNode.getFather() && insertNode.getFather().color == Node.RED && null != insertNode.getUncle() && insertNode.getUncle().color == Node.RED){
//爷爷红,叔叔爸爸黑,引用节点为爷爷,继续向上查找
redBlackBlack(insertNode.getGrandFather());
insertNode = insertNode.getGrandFather();
}else{
//父节点在爷爷左边
if(null != insertNode.getGrandFather() && insertNode.getGrandFather().left == insertNode.getFather()){ //左
if(insertNode == insertNode.getFather().left){ //左
//左左右旋
insertNode = rightRotate(insertNode.getFather());
}else{ //右
//先左旋,再右旋
insertNode = leftRotate(insertNode);
insertNode = rightRotate(insertNode);
}
}else{ //父节点在爷爷右边 //右
if(null != insertNode.getGrandFather() && insertNode == insertNode.getFather().left){ //左
insertNode = rightRotate(insertNode); //注意这里传入的方法,永远是要变成爸爸的儿子。返回的是新爸爸
insertNode = leftRotate(insertNode);
}else{ //右
insertNode = leftRotate(insertNode.getFather());
}
}
//旋转完成,重新染色!!
blackRedRed(insertNode);
}
}
setBlack(root);
}
/***
* 只有插入操作,只执行插入
* @param value 插入的值
* @return 插入完成后返回插入节点
*/
private Node doInsert(int value){
Node insertNode = new Node(value);
Node father = root;
Node tempFather = null;
while(father != null){
tempFather = father;
if(value < father.value){
father = father.left;
}else{
father = father.right;
}
}
if(value < tempFather.value){
tempFather.left = insertNode;
}else{
tempFather.right = insertNode;
}
insertNode.parent = tempFather;
return insertNode;
}
/***
* 对外开放insert
* @param value
* @throws Exception
*/
public void insert(Integer value) throws Exception {
//验证root初始化
if(null == root){
Node node = new Node(value);
setBlack(node);
this.root = node;
return;
}
//验证是否已插入节点
if(null != findValue(root,value)){
throw new Exception("不允许重复插入值");
}
Node insertNode = doInsert(value);
rebuildInsertCore(insertNode);
}
/****
* 插入之后重新构建红黑树
* @param insertNode
*/
private void rebuildInsertCore(Node insertNode){
while(null != insertNode.getFather() && insertNode.getFather().color == Node.RED && insertNode.color == Node.RED){
if(null != insertNode.getFather() && insertNode.getFather().color == Node.RED && null != insertNode.getUncle() && insertNode.getUncle().color == Node.RED){
//爷爷红,叔叔爸爸黑,引用节点为爷爷,继续向上查找
redBlackBlack(insertNode.getGrandFather());
insertNode = insertNode.getGrandFather();
}else{
//父节点在爷爷左边
if(null != insertNode.getGrandFather() && insertNode.getGrandFather().left == insertNode.getFather()){ //左
if(insertNode == insertNode.getFather().left){ //左
//左左右旋
insertNode = rightRotate(insertNode.getFather());
}else{ //右
//先左旋,再右旋
insertNode = leftRotate(insertNode);
insertNode = rightRotate(insertNode);
}
}else{ //父节点在爷爷右边 //右
if(null != insertNode.getGrandFather() && insertNode == insertNode.getFather().left){ //左
insertNode = rightRotate(insertNode); //注意这里传入的方法,永远是要变成爸爸的儿子。返回的是新爸爸
insertNode = leftRotate(insertNode);
}else{ //右
insertNode = leftRotate(insertNode.getFather());
}
}
//旋转完成,重新染色!!
blackRedRed(insertNode);
}
}
setBlack(root);
}- 先插入,然后进行颜色判定。
- 决定旋转和着色方案,调用相应的方法,博主将旋转和着色分离了
删除操作
/****
* 删除对外开放操作
* @param value 要删除的对象
* @throws Exception
*/
public void remove(int value) throws Exception {
Node removeNode;
if((removeNode = findValue(root,value)) == null){
throw new Exception("要删除的节点不存在!");
}
doRemove(removeNode);
}
/****
* 内部执行删除操作
* @param removeNode
*/
private void doRemove(Node removeNode){
if(null != removeNode.left && null != removeNode.right){ //左右都不为空的情况
//左边最大方案.找到替代节点,替换!转换思维删除单节点
Node replaceNode = removeNode.left;
while(replaceNode.right != null){
replaceNode = replaceNode.right;
}
String color = replaceNode.color;
//判断node节点是否为root节点
if(null == removeNode.getFather()){
this.root = replaceNode;
}else{
if(removeNode.getFather().left == removeNode){
removeNode.getFather().left = replaceNode;
}else{
removeNode.getFather().right = replaceNode;
}
}
replaceNode.color = removeNode.color;
//如果替换节点是直接子节点,那么则不用再指定相应方向的子节点了,否则无限关联
if(removeNode.left != replaceNode){
replaceNode.left = removeNode.left;
replaceNode.left.parent = replaceNode;
}
if(removeNode.right != replaceNode){
replaceNode.right = removeNode.right;
replaceNode.right.parent = replaceNode;
}
replaceNode.parent = removeNode.parent;
//如果替换节点的颜色是黑色,那么替换节点原来所在的地方应该已经丢失了一个黑色节点,
//此时就需要重新调整数目
if(color.equals(Node.BLACK)){
removeRebuildRB(replaceNode.left,replaceNode);
}
//删除
removeNode = null;
}else if(null != removeNode.left || null != removeNode.right){ //有一个儿子的情况
//子节点替换,变更颜色即可
removeSingleSon(removeNode);
removeNode = null;
}else{
//一个儿子也没有,并且是黑色的,需要重新修正红黑树
removeRebuildRB(removeNode,removeNode.getFather());
//黑色处理完删除!红色直接删除
if(removeNode.getFather().left == removeNode){
removeNode.getFather().left = null;
}else{
removeNode.getFather().right = null;
}
}
}
/***
* 删除只有一个儿子节点时
* -替换被删除节点的颜色
* -替换被删除节点的位置
* -绑定关系
*/
private void removeSingleSon(Node removeNode){
if(null != removeNode.left){ //左儿子不为空
removeNode.left.getGrandFather().left = removeNode.left;
removeNode.left.parent = removeNode.parent;
removeNode.left.color = removeNode.color;
}else if(null != removeNode.right){ //右儿子不为空的情况
removeNode.right.getGrandFather().right = removeNode.right;
removeNode.right.parent = removeNode.parent;
removeNode.right.color = removeNode.color;
}
}
/****
* 删除以后,重新构建一颗红黑树
* 1-删除的是一个单独的黑色节点,那么删除后,两边的黑色节点的数量很有可能不一致
*
*/
private Node removeRebuildRB(Node node,Node parent){
Node bro = null;
while(null == node || node.color == Node.BLACK){
if(node == parent.left){
bro = parent.right; //获取兄弟节点
if(null != bro && bro.color == Node.RED){
//情况一:要删除的节点为黑色,且在左边,兄弟节点在右边,红色
//,兄弟节点左旋
setBlack(bro);
setRed(parent);
leftRotate(bro);
bro = parent.right;
}
//情形2,兄弟置换兄弟节点和父节点的颜色节点为黑色;兄弟两个子节点都为黑色;
if ((bro.left == null || bro.left.color == Node.BLACK)
&& (bro.right == null || bro.right.color == Node.BLACK)){
setRed(bro); //要删除一个黑色节点,则兄弟节点也设置为红色,否则黑色数量不一致
node = parent; //设置node为上一层节点,继续查找
parent = parent.getFather(); //设置为上一层节点,继续向上查找
}else{
//情形3:删除的节点是黑色;兄弟节点是黑色;兄弟节点左孩子红色;兄弟节点右孩子黑色
if((bro.right == null || bro.right.color == Node.BLACK) && (null != bro.left && bro.left.color == Node.RED)){
//兄弟节点的左孩子是红色的,右节点是黑色
setBlack(bro.left);
setRed(bro);
rightRotate(bro.left);
bro = parent.right;
}
//情形4:删除的节点是黑色;兄弟节点是黑色的;并且兄弟节点右孩子是红色,左孩子任意颜色
bro.color = bro.getFather().color;
setBlack(bro.getFather());
setBlack(bro.right);
leftRotate(bro);
node = this.root;
break;
}
}else{ //要删除的节点在右侧
bro = parent.left;
if(null != bro && bro.color == Node.RED){
//情况一:要删除的节点为黑色,且在右边,兄弟节点在左边,红色
setBlack(bro);
setRed(parent);
rightRotate(bro);
bro = parent.right;
}
//情形2,兄弟置换兄弟节点和父节点的颜色节点为黑色;兄弟两个子节点都为黑色;
if ((bro.left == null || bro.left.color == Node.BLACK)
&& (bro.right == null || bro.right.color == Node.BLACK)){
setRed(bro); //要删除一个黑色节点,则兄弟节点也设置为红色,否则黑色数量不一致
node = parent; //设置node为上一层节点,继续查找
parent = parent.getFather();
}else{
//情形3:删除的节点是黑色;兄弟节点是黑色;兄弟节点左孩子红色;兄弟节点右孩子黑色
if((bro.right == null || bro.right.color == Node.BLACK) && (null != bro.left && bro.left.color == Node.RED)){
//兄弟节点的左孩子是红色的,右节点是黑色
setBlack(bro.right);
setRed(bro);
leftRotate(bro.right);
bro = parent.right;
}
//情形4:删除的节点是黑色;兄弟节点是黑色的;并且兄弟节点右孩子是红色,左孩子任意颜色
bro.color = bro.getFather().color;
setBlack(bro.getFather());
setBlack(bro.left);
rightRotate(bro);
node = this.root;
break;
}
}
}
//设置为黑色节点
setBlack(node);
return node;
}
/****
* 删除对外开放操作
* @param value 要删除的对象
* @throws Exception
*/
public void remove(int value) throws Exception {
Node removeNode;
if((removeNode = findValue(root,value)) == null){
throw new Exception("要删除的节点不存在!");
}
doRemove(removeNode);
}
/****
* 内部执行删除操作
* @param removeNode
*/
private void doRemove(Node removeNode){
if(null != removeNode.left && null != removeNode.right){ //左右都不为空的情况
//左边最大方案.找到替代节点,替换!转换思维删除单节点
Node replaceNode = removeNode.left;
while(replaceNode.right != null){
replaceNode = replaceNode.right;
}
String color = replaceNode.color;
//判断node节点是否为root节点
if(null == removeNode.getFather()){
this.root = replaceNode;
}else{
if(removeNode.getFather().left == removeNode){
removeNode.getFather().left = replaceNode;
}else{
removeNode.getFather().right = replaceNode;
}
}
replaceNode.color = removeNode.color;
//如果替换节点是直接子节点,那么则不用再指定相应方向的子节点了,否则无限关联
if(removeNode.left != replaceNode){
replaceNode.left = removeNode.left;
replaceNode.left.parent = replaceNode;
}
if(removeNode.right != replaceNode){
replaceNode.right = removeNode.right;
replaceNode.right.parent = replaceNode;
}
replaceNode.parent = removeNode.parent;
//如果替换节点的颜色是黑色,那么替换节点原来所在的地方应该已经丢失了一个黑色节点,
//此时就需要重新调整数目
if(color.equals(Node.BLACK)){
removeRebuildRB(replaceNode.left,replaceNode);
}
//删除
removeNode = null;
}else if(null != removeNode.left || null != removeNode.right){ //有一个儿子的情况
//子节点替换,变更颜色即可
removeSingleSon(removeNode);
removeNode = null;
}else{
//一个儿子也没有,并且是黑色的,需要重新修正红黑树
removeRebuildRB(removeNode,removeNode.getFather());
//黑色处理完删除!红色直接删除
if(removeNode.getFather().left == removeNode){
removeNode.getFather().left = null;
}else{
removeNode.getFather().right = null;
}
}
}
/***
* 删除只有一个儿子节点时
* -替换被删除节点的颜色
* -替换被删除节点的位置
* -绑定关系
*/
private void removeSingleSon(Node removeNode){
if(null != removeNode.left){ //左儿子不为空
removeNode.left.getGrandFather().left = removeNode.left;
removeNode.left.parent = removeNode.parent;
removeNode.left.color = removeNode.color;
}else if(null != removeNode.right){ //右儿子不为空的情况
removeNode.right.getGrandFather().right = removeNode.right;
removeNode.right.parent = removeNode.parent;
removeNode.right.color = removeNode.color;
}
}
/****
* 删除以后,重新构建一颗红黑树
* 1-删除的是一个单独的黑色节点,那么删除后,两边的黑色节点的数量很有可能不一致
*
*/
private Node removeRebuildRB(Node node,Node parent){
Node bro = null;
while(null == node || node.color == Node.BLACK){
if(node == parent.left){
bro = parent.right; //获取兄弟节点
if(null != bro && bro.color == Node.RED){
//情况一:要删除的节点为黑色,且在左边,兄弟节点在右边,红色
//,兄弟节点左旋
setBlack(bro);
setRed(parent);
leftRotate(bro);
bro = parent.right;
}
//情形2,兄弟置换兄弟节点和父节点的颜色节点为黑色;兄弟两个子节点都为黑色;
if ((bro.left == null || bro.left.color == Node.BLACK)
&& (bro.right == null || bro.right.color == Node.BLACK)){
setRed(bro); //要删除一个黑色节点,则兄弟节点也设置为红色,否则黑色数量不一致
node = parent; //设置node为上一层节点,继续查找
parent = parent.getFather(); //设置为上一层节点,继续向上查找
}else{
//情形3:删除的节点是黑色;兄弟节点是黑色;兄弟节点左孩子红色;兄弟节点右孩子黑色
if((bro.right == null || bro.right.color == Node.BLACK) && (null != bro.left && bro.left.color == Node.RED)){
//兄弟节点的左孩子是红色的,右节点是黑色
setBlack(bro.left);
setRed(bro);
rightRotate(bro.left);
bro = parent.right;
}
//情形4:删除的节点是黑色;兄弟节点是黑色的;并且兄弟节点右孩子是红色,左孩子任意颜色
bro.color = bro.getFather().color;
setBlack(bro.getFather());
setBlack(bro.right);
leftRotate(bro);
node = this.root;
break;
}
}else{ //要删除的节点在右侧
bro = parent.left;
if(null != bro && bro.color == Node.RED){
//情况一:要删除的节点为黑色,且在右边,兄弟节点在左边,红色
setBlack(bro);
setRed(parent);
rightRotate(bro);
bro = parent.right;
}
//情形2,兄弟置换兄弟节点和父节点的颜色节点为黑色;兄弟两个子节点都为黑色;
if ((bro.left == null || bro.left.color == Node.BLACK)
&& (bro.right == null || bro.right.color == Node.BLACK)){
setRed(bro); //要删除一个黑色节点,则兄弟节点也设置为红色,否则黑色数量不一致
node = parent; //设置node为上一层节点,继续查找
parent = parent.getFather();
}else{
//情形3:删除的节点是黑色;兄弟节点是黑色;兄弟节点左孩子红色;兄弟节点右孩子黑色
if((bro.right == null || bro.right.color == Node.BLACK) && (null != bro.left && bro.left.color == Node.RED)){
//兄弟节点的左孩子是红色的,右节点是黑色
setBlack(bro.right);
setRed(bro);
leftRotate(bro.right);
bro = parent.right;
}
//情形4:删除的节点是黑色;兄弟节点是黑色的;并且兄弟节点右孩子是红色,左孩子任意颜色
bro.color = bro.getFather().color;
setBlack(bro.getFather());
setBlack(bro.left);
rightRotate(bro);
node = this.root;
break;
}
}
}
//设置为黑色节点
setBlack(node);
return node;
}- doRemove方法为删除类型的转换
- removeRebuildRB为单一黑色节点删除以后的重构建,也是本篇最复杂的一个点
完整源码
- 本例是单类加内部类实现了所有功能,如不太理解的同学可以直接拿走运行尝试
- 博主加入了一种层级遍历操作,如需要其他遍历方式请自行查看上一篇AVL平衡二叉树详解
package focus.zhishui.tree.blackred;
import focus.zhishui.tree.AvlTreeInteger;
import java.util.ArrayList;
import java.util.List;
/**
* 红黑树Java实现
* Created by 止水 on 2018-09-14.
*/
public class RedBlackTree {
//基础Node信息
public static class Node{
public static final String RED = "red";
public static final String BLACK = "black";
public int value;
public String color; //方便理解,我们就用string
public Node left;
public Node right;
public Node parent;
public Node(int value) {
this.value = value;
initNode(value,Node.RED,null,null,parent);
}
public Node(int value, String color, Node left, Node right,Node parent) {
initNode(value,color,left,right,parent);
}
private void initNode(int value, String color, Node left, Node right,Node parent){
this.value = value;
this.color = color;
this.left = left;
this.right = right;
}
//获取父亲节点
public Node getFather(){
return this.parent;
}
//获取爸爸的兄弟节点
public Node getUncle(){
if(null == this.parent) return null;
if(null == this.parent.parent) return null;
if (this.parent == this.parent.parent.left){
return this.parent.parent.right;
}else{
return this.parent.parent.left;
}
}
/***
* 获取爷爷节点
* @return
*/
public Node getGrandFather(){
if(null == this.parent) return null;
return this.parent.parent;
}
/***
* 获取兄弟节点
* @return
*/
public Node getBro(){
if(null == this.parent) return null;
if(value == this.parent.left.value){
return this.parent.right;
}else{
return this.parent.left;
}
}
}
private Node root;
private int size;
public RedBlackTree(Node root) {
setBlack(root);
this.root = root;
}
public RedBlackTree() {
}
/***
* 设置节点为黑色
* @param node
*/
private void setBlack(Node node){
if(null != node){
node.color = Node.BLACK;
}
}
private void setRed(Node node){
if(null != node){
node.color = Node.RED;
}
}
/***
* 从父节点及其子节点中找value值
* @param father
* @param value
* @return
*/
private Node findValue(Node father,int value){
while(father != null){
if(value > father.value){
father = father.right;
}else if(value < father.value){
father = father.left;
}else{
return father;
}
}
return null;
}
/***
* 只有插入操作,只执行插入
* @param value 插入的值
* @return 插入完成后返回插入节点
*/
private Node doInsert(int value){
Node insertNode = new Node(value);
Node father = root;
Node tempFather = null;
while(father != null){
tempFather = father;
if(value < father.value){
father = father.left;
}else{
father = father.right;
}
}
if(value < tempFather.value){
tempFather.left = insertNode;
}else{
tempFather.right = insertNode;
}
insertNode.parent = tempFather;
return insertNode;
}
/***
* 对外开放insert
* @param value
* @throws Exception
*/
public void insert(Integer value) throws Exception {
//验证root初始化
if(null == root){
Node node = new Node(value);
setBlack(node);
this.root = node;
return;
}
//验证是否已插入节点
if(null != findValue(root,value)){
throw new Exception("不允许重复插入值");
}
Node insertNode = doInsert(value);
rebuildInsertCore(insertNode);
}
/***
* 右旋
* 右右类型传入父亲节点
* 左右类型传入儿子节点
* @param currentNode 传入的永远是要变成爸爸的儿子
* @Return node 返回最新的爸爸
*/
private Node rightRotate(Node currentNode){
//获取旋转前角色
Node grandFather = currentNode.getGrandFather();
Node father = currentNode.getFather();
//双方丢失的节点重新绑定
father.left = currentNode.right;
//绑定爷爷和父亲的角色
if(null != grandFather){
if(father == grandFather.left){
grandFather.left = currentNode;
}else{
grandFather.right = currentNode;
}
currentNode.parent = grandFather;
}else{ //替换root节点
this.root = currentNode;
currentNode.parent = null;
}
//儿子与父节点的关联
currentNode.right = father;
father.parent = currentNode;
return currentNode;
}
/****
* 左旋
* 右右类型传入父亲节点
* 左右类型传入儿子节点
* @param currentNode 传入的永远是要变成爸爸的儿子,
* @Return node 返回最新的爸爸
*/
private Node leftRotate(Node currentNode){
//获取旋转前角色
Node grandFather = currentNode.getGrandFather();
Node father = currentNode.getFather();
//双方丢失的节点重新绑定
father.right = currentNode.left;
//绑定爷爷和父亲的角色
if(null != grandFather){ //到root节点,则重新赋值root
if(father == grandFather.left){
grandFather.left = currentNode;
}else{
grandFather.right = currentNode;
}
currentNode.parent = grandFather;
}else{
root = currentNode;
currentNode.parent = null;
}
//儿子与父节点的关联
currentNode.left = father;
father.parent = currentNode;
return currentNode;
}
/****
* 红黑黑类型
* @param colorNode 传入固定时间的父亲节点
*/
private void redBlackBlack(Node colorNode){
setRed(colorNode);
setBlack(colorNode.left);
setBlack(colorNode.right);
}
/*****
* 黑红红类型
* @param colorNode 传入固定时间的父亲节点
*/
private void blackRedRed(Node colorNode){
setBlack(colorNode);
setRed(colorNode.left);
setRed(colorNode.right);
}
/****
* 插入之后重新构建红黑树
* @param insertNode
*/
private void rebuildInsertCore(Node insertNode){
while(null != insertNode.getFather() && insertNode.getFather().color == Node.RED && insertNode.color == Node.RED){
if(null != insertNode.getFather() && insertNode.getFather().color == Node.RED && null != insertNode.getUncle() && insertNode.getUncle().color == Node.RED){
//爷爷红,叔叔爸爸黑,引用节点为爷爷,继续向上查找
redBlackBlack(insertNode.getGrandFather());
insertNode = insertNode.getGrandFather();
}else{
//父节点在爷爷左边
if(null != insertNode.getGrandFather() && insertNode.getGrandFather().left == insertNode.getFather()){ //左
if(insertNode == insertNode.getFather().left){ //左
//左左右旋
insertNode = rightRotate(insertNode.getFather());
}else{ //右
//先左旋,再右旋
insertNode = leftRotate(insertNode);
insertNode = rightRotate(insertNode);
}
}else{ //父节点在爷爷右边 //右
if(null != insertNode.getGrandFather() && insertNode == insertNode.getFather().left){ //左
insertNode = rightRotate(insertNode); //注意这里传入的方法,永远是要变成爸爸的儿子。返回的是新爸爸
insertNode = leftRotate(insertNode);
}else{ //右
insertNode = leftRotate(insertNode.getFather());
}
}
//旋转完成,重新染色!!
blackRedRed(insertNode);
}
}
setBlack(root);
}
/****
* 删除对外开放操作
* @param value 要删除的对象
* @throws Exception
*/
public void remove(int value) throws Exception {
Node removeNode;
if((removeNode = findValue(root,value)) == null){
throw new Exception("要删除的节点不存在!");
}
doRemove(removeNode);
}
/****
* 内部执行删除操作
* @param removeNode
*/
private void doRemove(Node removeNode){
if(null != removeNode.left && null != removeNode.right){ //左右都不为空的情况
//左边最大方案.找到替代节点,替换!转换思维删除单节点
Node replaceNode = removeNode.left;
while(replaceNode.right != null){
replaceNode = replaceNode.right;
}
String color = replaceNode.color;
//判断node节点是否为root节点
if(null == removeNode.getFather()){
this.root = replaceNode;
}else{
if(removeNode.getFather().left == removeNode){
removeNode.getFather().left = replaceNode;
}else{
removeNode.getFather().right = replaceNode;
}
}
replaceNode.color = removeNode.color;
//如果替换节点是直接子节点,那么则不用再指定相应方向的子节点了,否则无限关联
if(removeNode.left != replaceNode){
replaceNode.left = removeNode.left;
replaceNode.left.parent = replaceNode;
}
if(removeNode.right != replaceNode){
replaceNode.right = removeNode.right;
replaceNode.right.parent = replaceNode;
}
replaceNode.parent = removeNode.parent;
//如果替换节点的颜色是黑色,那么替换节点原来所在的地方应该已经丢失了一个黑色节点,
//此时就需要重新调整数目
if(color.equals(Node.BLACK)){
removeRebuildRB(replaceNode.left,replaceNode);
}
//删除
removeNode = null;
}else if(null != removeNode.left || null != removeNode.right){ //有一个儿子的情况
//子节点替换,变更颜色即可
removeSingleSon(removeNode);
removeNode = null;
}else{
//一个儿子也没有,并且是黑色的,需要重新修正红黑树
removeRebuildRB(removeNode,removeNode.getFather());
//黑色处理完删除!红色直接删除
if(removeNode.getFather().left == removeNode){
removeNode.getFather().left = null;
}else{
removeNode.getFather().right = null;
}
}
}
/***
* 删除只有一个儿子节点时
* -替换被删除节点的颜色
* -替换被删除节点的位置
* -绑定关系
*/
private void removeSingleSon(Node removeNode){
if(null != removeNode.left){ //左儿子不为空
removeNode.left.getGrandFather().left = removeNode.left;
removeNode.left.parent = removeNode.parent;
removeNode.left.color = removeNode.color;
}else if(null != removeNode.right){ //右儿子不为空的情况
removeNode.right.getGrandFather().right = removeNode.right;
removeNode.right.parent = removeNode.parent;
removeNode.right.color = removeNode.color;
}
}
/****
* 删除以后,重新构建一颗红黑树
* 1-删除的是一个单独的黑色节点,那么删除后,两边的黑色节点的数量很有可能不一致
*
*/
private Node removeRebuildRB(Node node,Node parent){
Node bro = null;
while(null == node || node.color == Node.BLACK){
if(node == parent.left){
bro = parent.right; //获取兄弟节点
if(null != bro && bro.color == Node.RED){
//情况一:要删除的节点为黑色,且在左边,兄弟节点在右边,红色
//,兄弟节点左旋
setBlack(bro);
setRed(parent);
leftRotate(bro);
bro = parent.right;
}
//情形2,兄弟置换兄弟节点和父节点的颜色节点为黑色;兄弟两个子节点都为黑色;
if ((bro.left == null || bro.left.color == Node.BLACK)
&& (bro.right == null || bro.right.color == Node.BLACK)){
setRed(bro); //要删除一个黑色节点,则兄弟节点也设置为红色,否则黑色数量不一致
node = parent; //设置node为上一层节点,继续查找
parent = parent.getFather(); //设置为上一层节点,继续向上查找
}else{
//情形3:删除的节点是黑色;兄弟节点是黑色;兄弟节点左孩子红色;兄弟节点右孩子黑色
if((bro.right == null || bro.right.color == Node.BLACK) && (null != bro.left && bro.left.color == Node.RED)){
//兄弟节点的左孩子是红色的,右节点是黑色
setBlack(bro.left);
setRed(bro);
rightRotate(bro.left);
bro = parent.right;
}
//情形4:删除的节点是黑色;兄弟节点是黑色的;并且兄弟节点右孩子是红色,左孩子任意颜色
bro.color = bro.getFather().color;
setBlack(bro.getFather());
setBlack(bro.right);
leftRotate(bro);
node = this.root;
break;
}
}else{ //要删除的节点在右侧
bro = parent.left;
if(null != bro && bro.color == Node.RED){
//情况一:要删除的节点为黑色,且在右边,兄弟节点在左边,红色
setBlack(bro);
setRed(parent);
rightRotate(bro);
bro = parent.right;
}
//情形2,兄弟置换兄弟节点和父节点的颜色节点为黑色;兄弟两个子节点都为黑色;
if ((bro.left == null || bro.left.color == Node.BLACK)
&& (bro.right == null || bro.right.color == Node.BLACK)){
setRed(bro); //要删除一个黑色节点,则兄弟节点也设置为红色,否则黑色数量不一致
node = parent; //设置node为上一层节点,继续查找
parent = parent.getFather();
}else{
//情形3:删除的节点是黑色;兄弟节点是黑色;兄弟节点左孩子红色;兄弟节点右孩子黑色
if((bro.right == null || bro.right.color == Node.BLACK) && (null != bro.left && bro.left.color == Node.RED)){
//兄弟节点的左孩子是红色的,右节点是黑色
setBlack(bro.right);
setRed(bro);
leftRotate(bro.right);
bro = parent.right;
}
//情形4:删除的节点是黑色;兄弟节点是黑色的;并且兄弟节点右孩子是红色,左孩子任意颜色
bro.color = bro.getFather().color;
setBlack(bro.getFather());
setBlack(bro.left);
rightRotate(bro);
node = this.root;
break;
}
}
}
//设置为黑色节点
setBlack(node);
return node;
}
private void cengji(List<Node> parent){
if(null == parent || parent.size() == 0) return;
//打印当前层
List<Node> AvlNodeIntegers = new ArrayList<Node>();
int k = 0;
for(int i = 0 ; i < parent.size() ; i++){
Node currentNode = parent.get(i);
System.out.println(currentNode.value+","+currentNode.color);
if(null != currentNode.left){
AvlNodeIntegers.add(currentNode.left);
k++;
}
if(null != currentNode.right){
AvlNodeIntegers.add(currentNode.right);
k++;
}
}
System.out.println("--------------------------");
cengji(AvlNodeIntegers);
}
public void printGraph(int style) {
List a = new ArrayList<>();
a.add(root);
cengji(a);
}
public static void main(String[] args) throws Exception {
RedBlackTree.Node root = new RedBlackTree.Node(50);
RedBlackTree rbt = new RedBlackTree(root);
//int[] a = new int[]{51,52};
// int[] a = new int[]{11,12,13,14};
// int[] a = new int[]{9,8,7,6,5};
//int[] a = new int[]{15,100,25,65,80,51,43,44};
//情形4删除,删除51
// int[] a = new int[]{48,51,52,53,54};
//情形3删除,先删除80,就到达了我们所说的情形3 51,48,52,80,60
// rbt.remove(80);
// rbt.remove(48);
// int[] a = new int[]{48,52,80,60};
//情形1删除 50,51,52,53,54,55
//int[] a = new int[]{51,52,53,54,55};
//情形2删除是旋转过程中出现的情况。
//删除以后变身情形2;
//广度测试
//50,51,52,53,54,55,56,49,48,47,46,45
int[] a = new int[]{51,52,53,54,55,56,49,48,47,46,45};
for(int i = 0 ; i < a.length ; i++){
try {
rbt.insert(a[i]);
} catch (Exception e) {
e.printStackTrace();
}
}
rbt.remove(52);
rbt.printGraph(4);
}
}
package focus.zhishui.tree.blackred;
import focus.zhishui.tree.AvlTreeInteger;
import java.util.ArrayList;
import java.util.List;
/**
* 红黑树Java实现
* Created by 止水 on 2018-09-14.
*/
public class RedBlackTree {
//基础Node信息
public static class Node{
public static final String RED = "red";
public static final String BLACK = "black";
public int value;
public String color; //方便理解,我们就用string
public Node left;
public Node right;
public Node parent;
public Node(int value) {
this.value = value;
initNode(value,Node.RED,null,null,parent);
}
public Node(int value, String color, Node left, Node right,Node parent) {
initNode(value,color,left,right,parent);
}
private void initNode(int value, String color, Node left, Node right,Node parent){
this.value = value;
this.color = color;
this.left = left;
this.right = right;
}
//获取父亲节点
public Node getFather(){
return this.parent;
}
//获取爸爸的兄弟节点
public Node getUncle(){
if(null == this.parent) return null;
if(null == this.parent.parent) return null;
if (this.parent == this.parent.parent.left){
return this.parent.parent.right;
}else{
return this.parent.parent.left;
}
}
/***
* 获取爷爷节点
* @return
*/
public Node getGrandFather(){
if(null == this.parent) return null;
return this.parent.parent;
}
/***
* 获取兄弟节点
* @return
*/
public Node getBro(){
if(null == this.parent) return null;
if(value == this.parent.left.value){
return this.parent.right;
}else{
return this.parent.left;
}
}
}
private Node root;
private int size;
public RedBlackTree(Node root) {
setBlack(root);
this.root = root;
}
public RedBlackTree() {
}
/***
* 设置节点为黑色
* @param node
*/
private void setBlack(Node node){
if(null != node){
node.color = Node.BLACK;
}
}
private void setRed(Node node){
if(null != node){
node.color = Node.RED;
}
}
/***
* 从父节点及其子节点中找value值
* @param father
* @param value
* @return
*/
private Node findValue(Node father,int value){
while(father != null){
if(value > father.value){
father = father.right;
}else if(value < father.value){
father = father.left;
}else{
return father;
}
}
return null;
}
/***
* 只有插入操作,只执行插入
* @param value 插入的值
* @return 插入完成后返回插入节点
*/
private Node doInsert(int value){
Node insertNode = new Node(value);
Node father = root;
Node tempFather = null;
while(father != null){
tempFather = father;
if(value < father.value){
father = father.left;
}else{
father = father.right;
}
}
if(value < tempFather.value){
tempFather.left = insertNode;
}else{
tempFather.right = insertNode;
}
insertNode.parent = tempFather;
return insertNode;
}
/***
* 对外开放insert
* @param value
* @throws Exception
*/
public void insert(Integer value) throws Exception {
//验证root初始化
if(null == root){
Node node = new Node(value);
setBlack(node);
this.root = node;
return;
}
//验证是否已插入节点
if(null != findValue(root,value)){
throw new Exception("不允许重复插入值");
}
Node insertNode = doInsert(value);
rebuildInsertCore(insertNode);
}
/***
* 右旋
* 右右类型传入父亲节点
* 左右类型传入儿子节点
* @param currentNode 传入的永远是要变成爸爸的儿子
* @Return node 返回最新的爸爸
*/
private Node rightRotate(Node currentNode){
//获取旋转前角色
Node grandFather = currentNode.getGrandFather();
Node father = currentNode.getFather();
//双方丢失的节点重新绑定
father.left = currentNode.right;
//绑定爷爷和父亲的角色
if(null != grandFather){
if(father == grandFather.left){
grandFather.left = currentNode;
}else{
grandFather.right = currentNode;
}
currentNode.parent = grandFather;
}else{ //替换root节点
this.root = currentNode;
currentNode.parent = null;
}
//儿子与父节点的关联
currentNode.right = father;
father.parent = currentNode;
return currentNode;
}
/****
* 左旋
* 右右类型传入父亲节点
* 左右类型传入儿子节点
* @param currentNode 传入的永远是要变成爸爸的儿子,
* @Return node 返回最新的爸爸
*/
private Node leftRotate(Node currentNode){
//获取旋转前角色
Node grandFather = currentNode.getGrandFather();
Node father = currentNode.getFather();
//双方丢失的节点重新绑定
father.right = currentNode.left;
//绑定爷爷和父亲的角色
if(null != grandFather){ //到root节点,则重新赋值root
if(father == grandFather.left){
grandFather.left = currentNode;
}else{
grandFather.right = currentNode;
}
currentNode.parent = grandFather;
}else{
root = currentNode;
currentNode.parent = null;
}
//儿子与父节点的关联
currentNode.left = father;
father.parent = currentNode;
return currentNode;
}
/****
* 红黑黑类型
* @param colorNode 传入固定时间的父亲节点
*/
private void redBlackBlack(Node colorNode){
setRed(colorNode);
setBlack(colorNode.left);
setBlack(colorNode.right);
}
/*****
* 黑红红类型
* @param colorNode 传入固定时间的父亲节点
*/
private void blackRedRed(Node colorNode){
setBlack(colorNode);
setRed(colorNode.left);
setRed(colorNode.right);
}
/****
* 插入之后重新构建红黑树
* @param insertNode
*/
private void rebuildInsertCore(Node insertNode){
while(null != insertNode.getFather() && insertNode.getFather().color == Node.RED && insertNode.color == Node.RED){
if(null != insertNode.getFather() && insertNode.getFather().color == Node.RED && null != insertNode.getUncle() && insertNode.getUncle().color == Node.RED){
//爷爷红,叔叔爸爸黑,引用节点为爷爷,继续向上查找
redBlackBlack(insertNode.getGrandFather());
insertNode = insertNode.getGrandFather();
}else{
//父节点在爷爷左边
if(null != insertNode.getGrandFather() && insertNode.getGrandFather().left == insertNode.getFather()){ //左
if(insertNode == insertNode.getFather().left){ //左
//左左右旋
insertNode = rightRotate(insertNode.getFather());
}else{ //右
//先左旋,再右旋
insertNode = leftRotate(insertNode);
insertNode = rightRotate(insertNode);
}
}else{ //父节点在爷爷右边 //右
if(null != insertNode.getGrandFather() && insertNode == insertNode.getFather().left){ //左
insertNode = rightRotate(insertNode); //注意这里传入的方法,永远是要变成爸爸的儿子。返回的是新爸爸
insertNode = leftRotate(insertNode);
}else{ //右
insertNode = leftRotate(insertNode.getFather());
}
}
//旋转完成,重新染色!!
blackRedRed(insertNode);
}
}
setBlack(root);
}
/****
* 删除对外开放操作
* @param value 要删除的对象
* @throws Exception
*/
public void remove(int value) throws Exception {
Node removeNode;
if((removeNode = findValue(root,value)) == null){
throw new Exception("要删除的节点不存在!");
}
doRemove(removeNode);
}
/****
* 内部执行删除操作
* @param removeNode
*/
private void doRemove(Node removeNode){
if(null != removeNode.left && null != removeNode.right){ //左右都不为空的情况
//左边最大方案.找到替代节点,替换!转换思维删除单节点
Node replaceNode = removeNode.left;
while(replaceNode.right != null){
replaceNode = replaceNode.right;
}
String color = replaceNode.color;
//判断node节点是否为root节点
if(null == removeNode.getFather()){
this.root = replaceNode;
}else{
if(removeNode.getFather().left == removeNode){
removeNode.getFather().left = replaceNode;
}else{
removeNode.getFather().right = replaceNode;
}
}
replaceNode.color = removeNode.color;
//如果替换节点是直接子节点,那么则不用再指定相应方向的子节点了,否则无限关联
if(removeNode.left != replaceNode){
replaceNode.left = removeNode.left;
replaceNode.left.parent = replaceNode;
}
if(removeNode.right != replaceNode){
replaceNode.right = removeNode.right;
replaceNode.right.parent = replaceNode;
}
replaceNode.parent = removeNode.parent;
//如果替换节点的颜色是黑色,那么替换节点原来所在的地方应该已经丢失了一个黑色节点,
//此时就需要重新调整数目
if(color.equals(Node.BLACK)){
removeRebuildRB(replaceNode.left,replaceNode);
}
//删除
removeNode = null;
}else if(null != removeNode.left || null != removeNode.right){ //有一个儿子的情况
//子节点替换,变更颜色即可
removeSingleSon(removeNode);
removeNode = null;
}else{
//一个儿子也没有,并且是黑色的,需要重新修正红黑树
removeRebuildRB(removeNode,removeNode.getFather());
//黑色处理完删除!红色直接删除
if(removeNode.getFather().left == removeNode){
removeNode.getFather().left = null;
}else{
removeNode.getFather().right = null;
}
}
}
/***
* 删除只有一个儿子节点时
* -替换被删除节点的颜色
* -替换被删除节点的位置
* -绑定关系
*/
private void removeSingleSon(Node removeNode){
if(null != removeNode.left){ //左儿子不为空
removeNode.left.getGrandFather().left = removeNode.left;
removeNode.left.parent = removeNode.parent;
removeNode.left.color = removeNode.color;
}else if(null != removeNode.right){ //右儿子不为空的情况
removeNode.right.getGrandFather().right = removeNode.right;
removeNode.right.parent = removeNode.parent;
removeNode.right.color = removeNode.color;
}
}
/****
* 删除以后,重新构建一颗红黑树
* 1-删除的是一个单独的黑色节点,那么删除后,两边的黑色节点的数量很有可能不一致
*
*/
private Node removeRebuildRB(Node node,Node parent){
Node bro = null;
while(null == node || node.color == Node.BLACK){
if(node == parent.left){
bro = parent.right; //获取兄弟节点
if(null != bro && bro.color == Node.RED){
//情况一:要删除的节点为黑色,且在左边,兄弟节点在右边,红色
//,兄弟节点左旋
setBlack(bro);
setRed(parent);
leftRotate(bro);
bro = parent.right;
}
//情形2,兄弟置换兄弟节点和父节点的颜色节点为黑色;兄弟两个子节点都为黑色;
if ((bro.left == null || bro.left.color == Node.BLACK)
&& (bro.right == null || bro.right.color == Node.BLACK)){
setRed(bro); //要删除一个黑色节点,则兄弟节点也设置为红色,否则黑色数量不一致
node = parent; //设置node为上一层节点,继续查找
parent = parent.getFather(); //设置为上一层节点,继续向上查找
}else{
//情形3:删除的节点是黑色;兄弟节点是黑色;兄弟节点左孩子红色;兄弟节点右孩子黑色
if((bro.right == null || bro.right.color == Node.BLACK) && (null != bro.left && bro.left.color == Node.RED)){
//兄弟节点的左孩子是红色的,右节点是黑色
setBlack(bro.left);
setRed(bro);
rightRotate(bro.left);
bro = parent.right;
}
//情形4:删除的节点是黑色;兄弟节点是黑色的;并且兄弟节点右孩子是红色,左孩子任意颜色
bro.color = bro.getFather().color;
setBlack(bro.getFather());
setBlack(bro.right);
leftRotate(bro);
node = this.root;
break;
}
}else{ //要删除的节点在右侧
bro = parent.left;
if(null != bro && bro.color == Node.RED){
//情况一:要删除的节点为黑色,且在右边,兄弟节点在左边,红色
setBlack(bro);
setRed(parent);
rightRotate(bro);
bro = parent.right;
}
//情形2,兄弟置换兄弟节点和父节点的颜色节点为黑色;兄弟两个子节点都为黑色;
if ((bro.left == null || bro.left.color == Node.BLACK)
&& (bro.right == null || bro.right.color == Node.BLACK)){
setRed(bro); //要删除一个黑色节点,则兄弟节点也设置为红色,否则黑色数量不一致
node = parent; //设置node为上一层节点,继续查找
parent = parent.getFather();
}else{
//情形3:删除的节点是黑色;兄弟节点是黑色;兄弟节点左孩子红色;兄弟节点右孩子黑色
if((bro.right == null || bro.right.color == Node.BLACK) && (null != bro.left && bro.left.color == Node.RED)){
//兄弟节点的左孩子是红色的,右节点是黑色
setBlack(bro.right);
setRed(bro);
leftRotate(bro.right);
bro = parent.right;
}
//情形4:删除的节点是黑色;兄弟节点是黑色的;并且兄弟节点右孩子是红色,左孩子任意颜色
bro.color = bro.getFather().color;
setBlack(bro.getFather());
setBlack(bro.left);
rightRotate(bro);
node = this.root;
break;
}
}
}
//设置为黑色节点
setBlack(node);
return node;
}
private void cengji(List<Node> parent){
if(null == parent || parent.size() == 0) return;
//打印当前层
List<Node> AvlNodeIntegers = new ArrayList<Node>();
int k = 0;
for(int i = 0 ; i < parent.size() ; i++){
Node currentNode = parent.get(i);
System.out.println(currentNode.value+","+currentNode.color);
if(null != currentNode.left){
AvlNodeIntegers.add(currentNode.left);
k++;
}
if(null != currentNode.right){
AvlNodeIntegers.add(currentNode.right);
k++;
}
}
System.out.println("--------------------------");
cengji(AvlNodeIntegers);
}
public void printGraph(int style) {
List a = new ArrayList<>();
a.add(root);
cengji(a);
}
public static void main(String[] args) throws Exception {
RedBlackTree.Node root = new RedBlackTree.Node(50);
RedBlackTree rbt = new RedBlackTree(root);
//int[] a = new int[]{51,52};
// int[] a = new int[]{11,12,13,14};
// int[] a = new int[]{9,8,7,6,5};
//int[] a = new int[]{15,100,25,65,80,51,43,44};
//情形4删除,删除51
// int[] a = new int[]{48,51,52,53,54};
//情形3删除,先删除80,就到达了我们所说的情形3 51,48,52,80,60
// rbt.remove(80);
// rbt.remove(48);
// int[] a = new int[]{48,52,80,60};
//情形1删除 50,51,52,53,54,55
//int[] a = new int[]{51,52,53,54,55};
//情形2删除是旋转过程中出现的情况。
//删除以后变身情形2;
//广度测试
//50,51,52,53,54,55,56,49,48,47,46,45
int[] a = new int[]{51,52,53,54,55,56,49,48,47,46,45};
for(int i = 0 ; i < a.length ; i++){
try {
rbt.insert(a[i]);
} catch (Exception e) {
e.printStackTrace();
}
}
rbt.remove(52);
rbt.printGraph(4);
}
}总结
以上就是红黑树的完整案例了,其中旋转,着色重新修正为红黑树比较核心,删除单一黑色节点的情况最为复杂。需要耐心多看一看。写下来以后发现与AVL树有以下几点区别,特此记录
- AVL树靠高度平衡,红黑树靠颜色特性平衡
- AVL数修正过程,每一层的高度都要进行判定,红黑树遇到黑色节点则结束判定,这样一来,红黑树在修正做的操作要优于AVL树
- 旋转原理都一样,但是AVL旋转完成后要重置高度,红黑旋转完成以后要重新着色
- 删除单一黑色节点后,修正的情况有很多,比较复杂。





















