目录
1.冒泡排序
2.选择排序
3.插入排序
4.希尔排序
5.归并排序
6.快速排序
1.冒泡排序
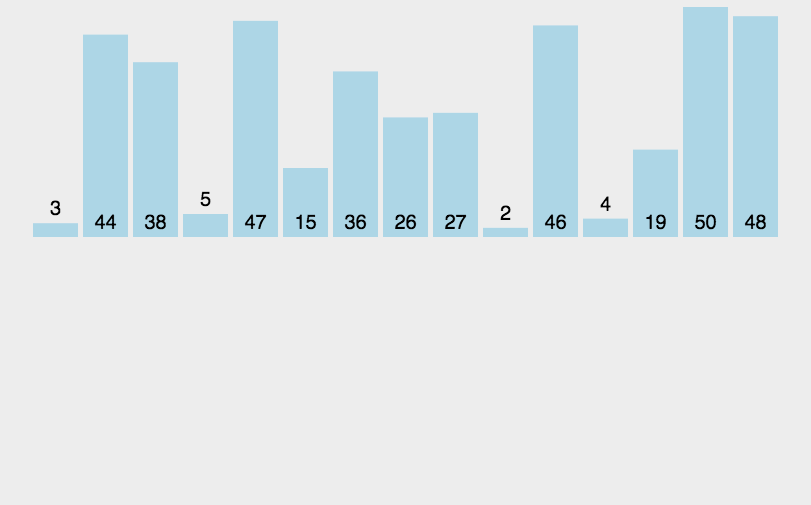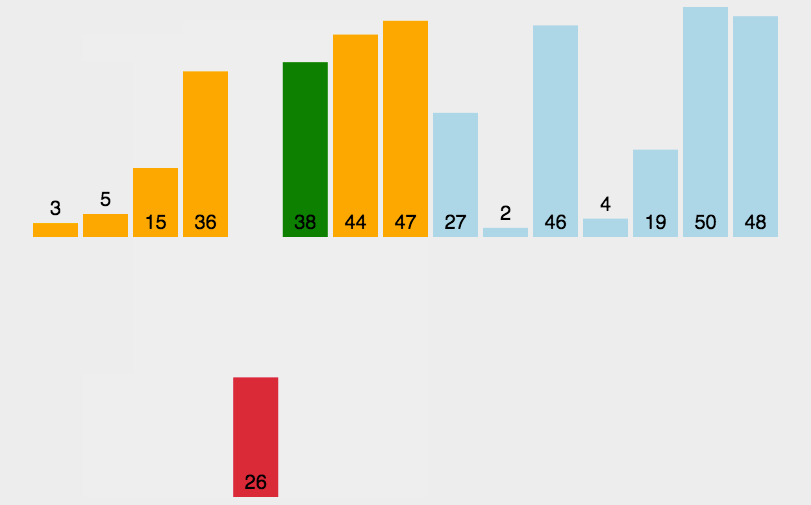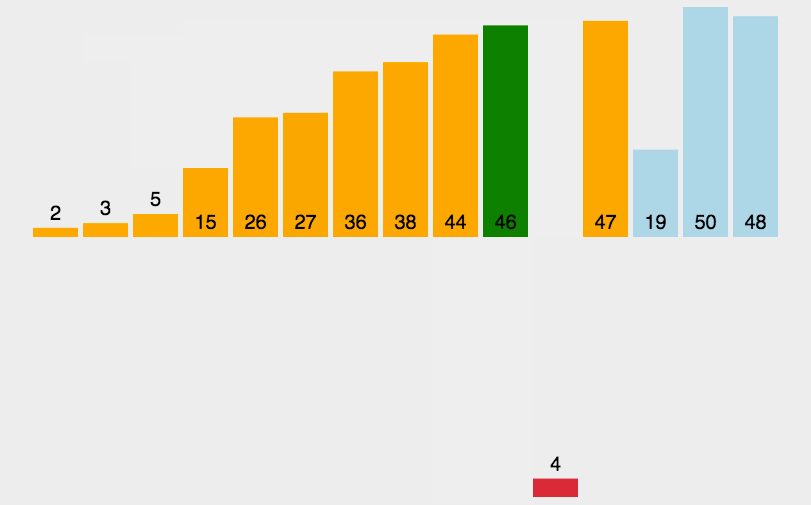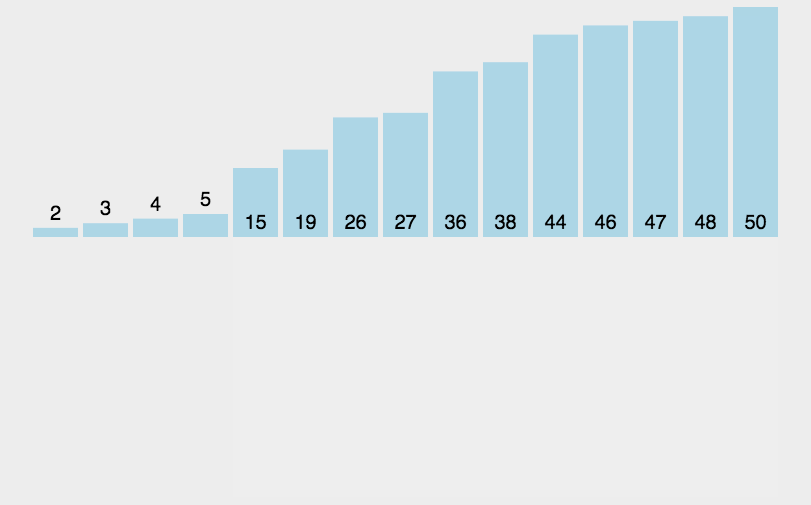
//冒泡排序
public class Bubble {
/**
* 对数组a中的元素进行冒泡排序
*/
public static void sort(Comparable[] a){
for(int i=a.length-1;i>0;i--){
for(int j=0;j<i;j++){
//比较索引j与索引j+1处得值
if(greater(a[j],a[j+1])){
exch(a,j,j+1);
}
}
}
}
/**
* 比较v元素是否大于w元素
*/
private static boolean greater(Comparable v,Comparable w){
return v.compareTo(w)>0;
}
/**
* 数组元素元素i和j交换位置
*/
private static void exch(Comparable[] a,int i,int j){
Comparable temp;
temp=a[i];
a[i]=a[j];
a[j]=temp;
}
}2.选择排序
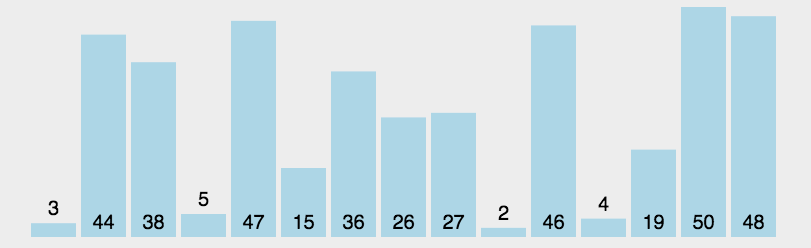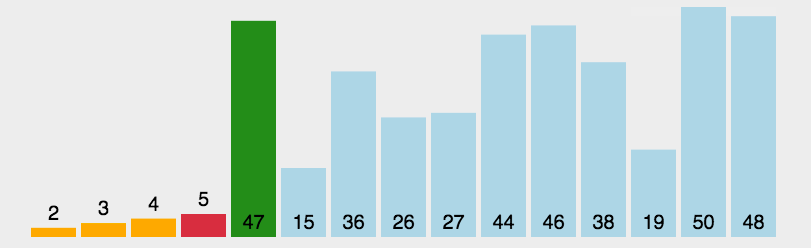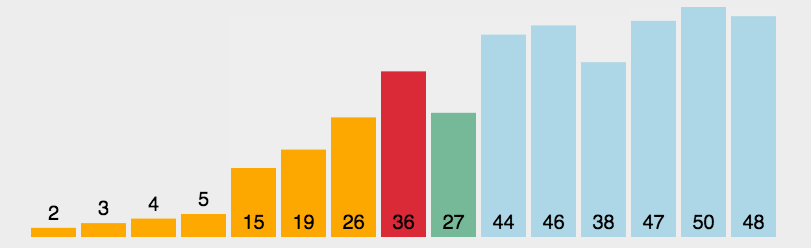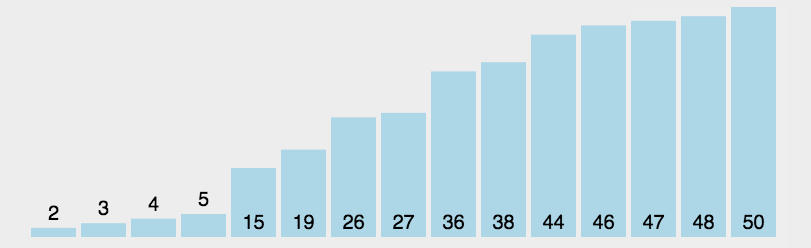
public class Selection {
/**
* 对数组中的元素进行选择排序
*/
public static void sort(Comparable[] a){
for(int i=0;i<a.length-1;i++){
//定义一个变量,记录最小元素所在的索引,默认为参与选择的第一个元素所在的位置
int minIndex=i;
for(int j=i+1;j<a.length;j++){
//比较索引minIndex处的值与j索引的值
if(greater(a[minIndex],a[j])){
minIndex=j;
}
}
//交换最小元素所在索引minIndex处的值和索引i处的值
exch(a,i,minIndex);
}
}
/**
* 比较v元素是否大于w元素
*/
public static boolean greater(Comparable v,Comparable w){
return v.compareTo(w)>0;
}
/**
* 数组元素i和j交换位置
*/
public static void exch(Comparable[] a,int i,int j){
Comparable temp;
temp=a[i];
a[i]=a[j];
a[j]=temp;
}
}3.插入排序
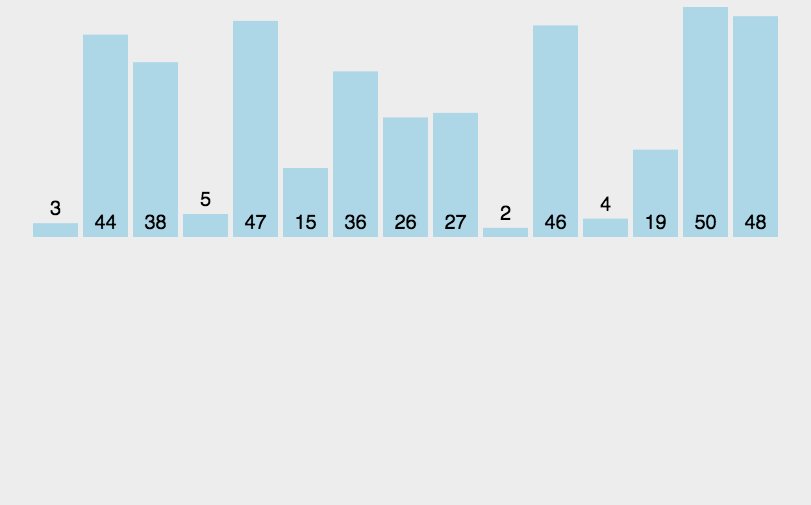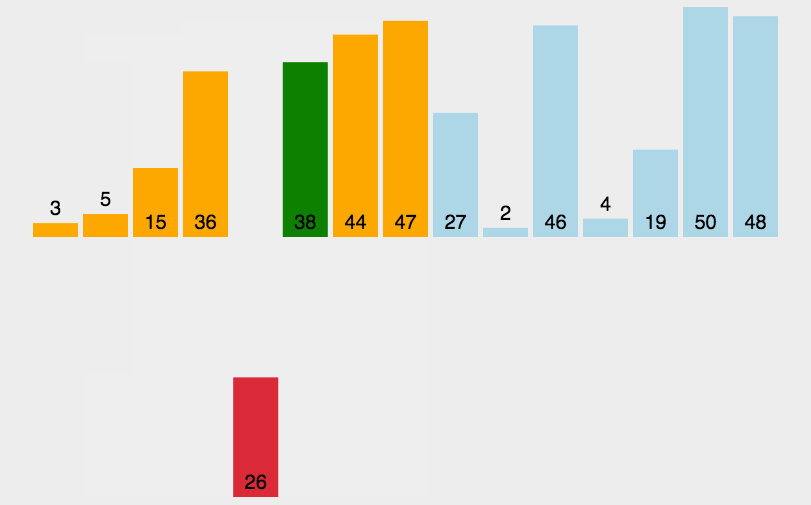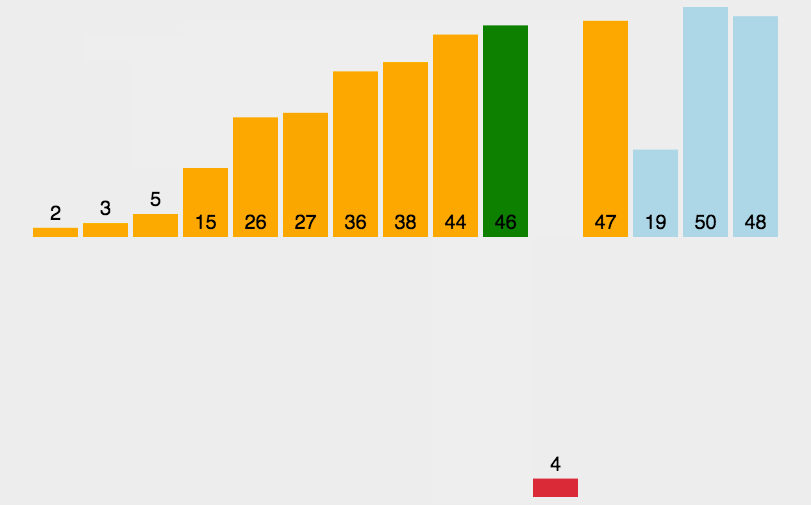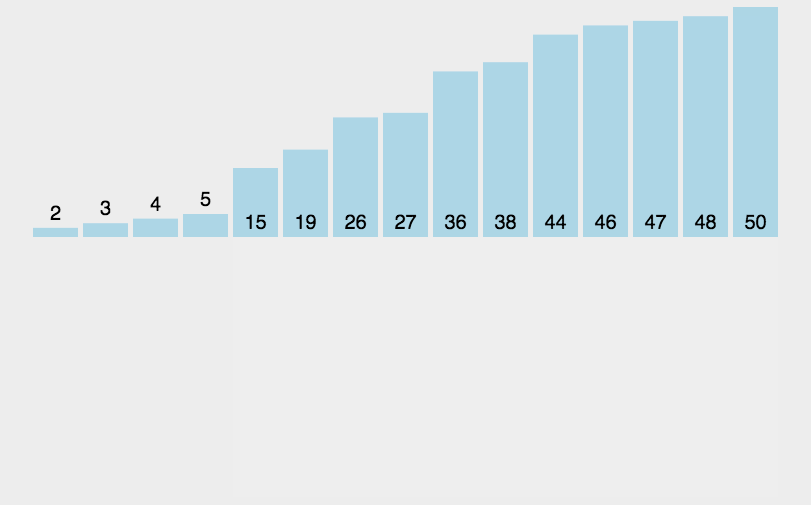
public class Insertion {
/**
* 对数组a中元素进行插入排序
*/
public static void sort(Comparable a[]){
for(int i=1;i<a.length;i++){
for(int j=i;j>0;j--){
if(greater(a[j-1],a[j])){
exch(a,j-1,j);
}else{
break;
}
}
}
}
/**
* 比较v元素是否大于w元素
*/
public static boolean greater(Comparable v,Comparable w){
return v.compareTo(w)>0;
}
/**
* 数组元素i和j进行交换
*/
public static void exch(Comparable[] a,int i,int j){
Comparable temp;
temp=a[i];
a[i]=a[j];
a[j]=temp;
}
}4.希尔排序
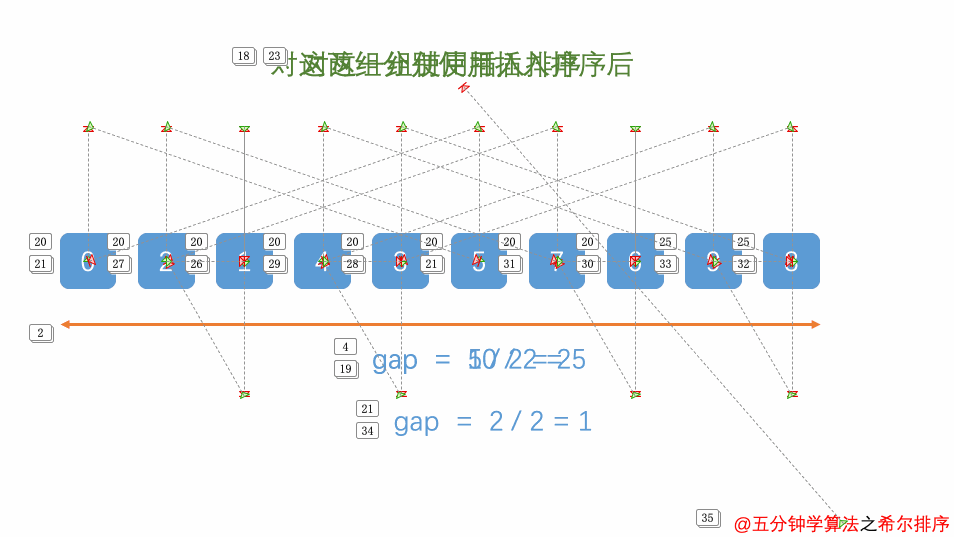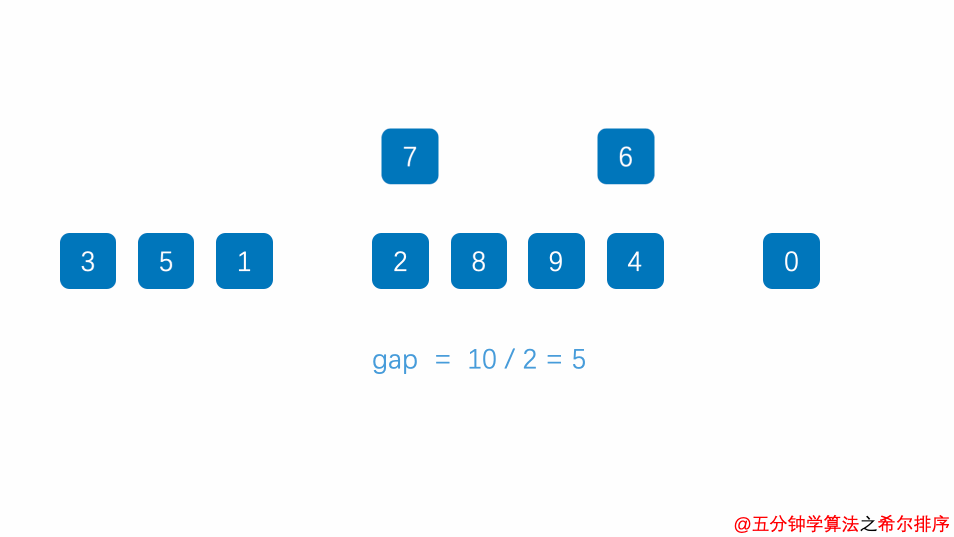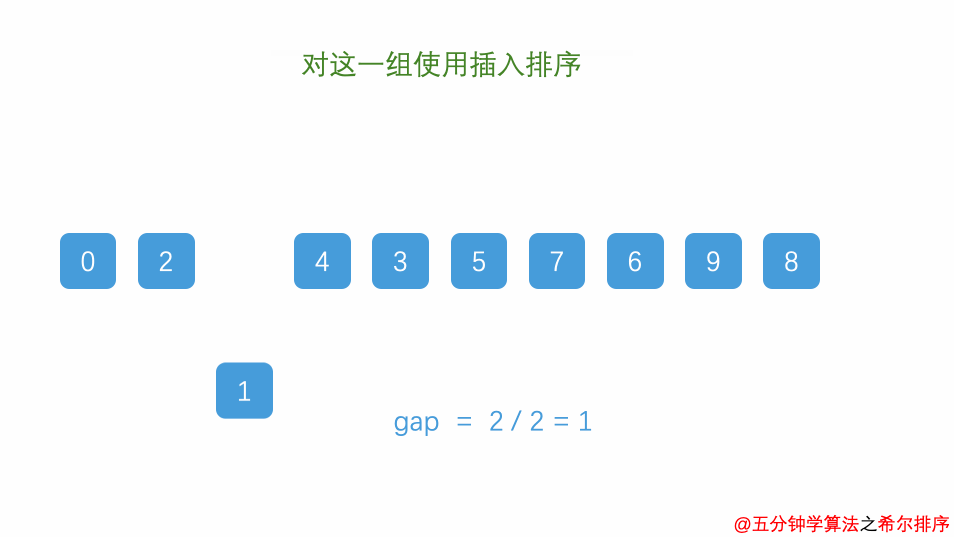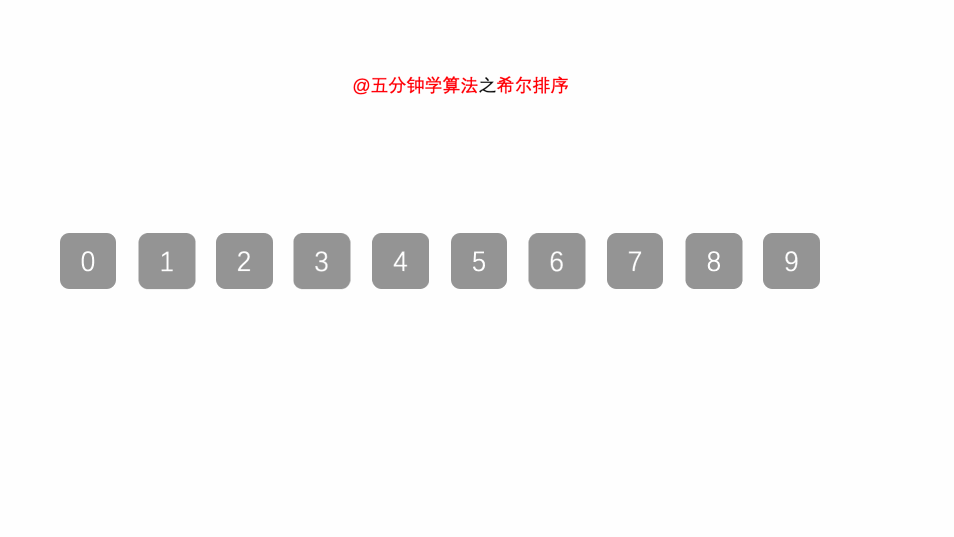
public class Shell {
/**
* 对数组a进行希尔排序
*/
public static void sort(Comparable[] a){
//1.根据数组a的长度,确定增长量h的初始值
int h=1;
while(h<a.length/2){
h=2*h+1;
}
//2.希尔排序
while(h>=1){
//排序
//2.1.找到待插入的元素
for(int i=h;i<a.length;i++){
//2.2.把待插入的元素插入有序数列中
for(int j=i;j>=h;j-=h){
//待插入的元素是a[j],比较a[j]和a[j-h]
if(greater(a[j-h],a[j])){
exch(a,j-h,j);
}
else{
//待插入元素已经找到合适位置,退出循环
break;
}
}
}
//减小h的值
h=h/2;
}
}
/**
* 比较v和w大小
*/
public static boolean greater(Comparable v,Comparable w){
return v.compareTo(w)>0;
}
/**
* 数组元素i和j交换
*/
public static void exch(Comparable[] a,int i,int j){
Comparable temp;
temp=a[i];
a[i]=a[j];
a[j]=temp;
}
}5.归并排序

public class Merge {
//归并所需要的辅助数组
private static Comparable[] assist;
/**
* 比较v元素是否小于w元素
*/
private static boolean less(Comparable v,Comparable w){
return v.compareTo(w)<0;
}
/**
* 数组元素i和j交换位置
*/
private static void exch(Comparable[] a,int i,int j){
Comparable temp;
temp=a[i];
a[i]=a[j];
a[j]=temp;
}
/**
* 对数组a中的元素进行排序
*/
public static void sort(Comparable[] a){
//1.初始化辅助数组 assist
assist=new Comparable[a.length];
//2.定义一个lo和hi变量,分别记录数组中最小的索引和最大的索引
int lo=0;
int hi=a.length-1;
//3.调用sort重载方法完成数组a中,从索引lo到hi的元素的排序
sort(a,lo,hi);
}
/**
* 对数组中lo到hi的元素进行排序
*/
public static void sort(Comparable[] a,int lo,int hi){
//做安全性校验
if(hi<=lo){
return;
}
//对lo到hi之间数据进行分组
int mid=lo+(hi-lo)/2; //5 9 mid=7
//分别对每一组数据进行排序
sort(a,lo,mid);
sort(a,mid+1,hi);
//再把两个组的数据进行归并
merge(a,lo,mid,hi);
}
/**
* 对数组中,从lo到mid为一组,从mid+1到hi为一组,对这两组数据进行归并
*/
public static void merge(Comparable[] a,int lo,int mid,int hi){
//定义三个指针
int i=lo;
int p1=lo;
int p2=mid+1;
//遍历,移动p1指针和p2指针,比较对应索引处的值,找出小的那个,放到辅助数组的对应索引处
while(p1<=mid && p2<=hi){
//比较对应索引处的值
if(less(a[p1],a[p2])){
assist[i++]=a[p1++];
}else{
assist[i++]=a[p2++];
}
}
//遍历,如果p1指针没有走完,那么顺序移动p1指针,把对应的元素放到辅助数组对应索引处
while (p1<=mid){
assist[i++]=a[p1++];
}
//遍历,如果p2指针没有走完,那么顺序移动p2指针,把对应的元素放到辅助数组对应索引处
while(p2<=hi){
assist[i++]=a[p2++];
}
//把辅助数组中的元素拷贝到原数组中
for (int index=lo;index<=hi;index++){
a[index]=assist[index];
}
}
}6.快速排序

public class Quick {
/**
* 比较v是否小于w
*/
public static boolean less(Comparable v,Comparable w){
return v.compareTo(w)<0;
}
/**
* 交换数组元素i和j的位置
*/
public static void exch(Comparable[] a,int i,int j){
Comparable temp=a[i];
a[i]=a[j];
a[j]=temp;
}
/**
* 对数组内的元素进行排序
*/
public static void sort(Comparable[] a){
int lo=0;
int hi=a.length-1;
sort(a,lo,hi);
}
/**
* 对数组中元素从索引lo到hi之间的元素进行排序
*/
public static void sort(Comparable[] a,int lo,int hi){
//安全性校验
if (hi<=lo){
return;
}
//需要对数组中lo索引到hi索引处的元素进行分组(左子组,右子组)
int partition=partition(a,lo,hi); //返回的是分组的分界值所在的索引,分界值变换后的索引
//左子组有序
sort(a,lo,partition-1);
//右子组有序
sort(a,partition+1,hi);
}
/**
* 对数组a中,从索引lo到hi之间的元素进行分组,并返回分组界限对应的索引
*/
public static int partition(Comparable[] a,int lo,int hi){
//确定分界值
Comparable key=a[lo];
//定义两个指针,分别指向待切分元素最小索引处和最大索引处的下一个位置
int left=lo;
int right=hi+1;
//切分
while(true){
//先从右往左扫描,移动right指针,找到比分界值小的元素,停止
while(less(key,a[--right])){
if(right==lo){
break;
}
}
//从左往右扫描,移动left指针,找到比分界值大的元素,停止
while(less(a[++left],key)){
if (left==hi){
break;
}
}
//判断left>=right,如果是,则证明元素扫描完毕,结束循环,如果不是,则交换元素即可
if (left>=right){
break;
}else{
exch(a,left,right);
}
}
//交换分界值
exch(a,lo,right);
return right;
}
}






















