Game of Connections HDU - 1134

 Game of Connections

 HDU - 1134 

This is a small but ancient game. You are supposed to write down the numbers 1, 2, 3, ... , 2n - 1, 2n consecutively in clockwise order on the ground to form a circle, and then, to draw some straight line segments to connect them into number pairs. Every number must be connected to exactly one another. And, no two segments are allowed to intersect. 

It's still a simple game, isn't it? But after you've written down the 2n numbers, can you tell me in how many different ways can you connect the numbers into pairs? Life is harder, right? 

Input

Each line of the input file will be a single positive number n, except the last line, which is a number -1. You may assume that 1 <= n <= 100. 

Output

For each n, print in a single line the number of ways to connect the 2n numbers into pairs. 

Sample Input

2
3
-1

Sample Output

2
5

题目大意：

给定2n 个点，围城一圈，问你把所有点一一成对连接，且不想交的个数有多少种方法？

思路：

卡特兰数，对应的递推公式如下

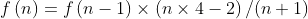
注意这里需要用到大数乘法和加法

 

#include<iostream>
#include<cstring>
using namespace std;
const int M = 10000;
const int N=100;
int arr[110][110] ={0};

//乘法，模拟乘法即可 
void multiply(int a[],int n,int b){
	int temp = 0;
	for(int i=n-1;i>=0;i--){
		temp += a[i]*b;
		a[i] =temp%M;
		temp/=M;
	}
} 
//除法，模拟小数除法即可 
void divide(int a[],int n,int b){
	int temp=0;
	for(int i=0;i<n;i++){
		temp = temp*M + a[i];
		a[i] = temp/b;
		temp %= b; 
	}
}
//初始化，先进行计算 
void init(){
	memset(arr[1],0,sizeof(arr[1]));
	arr[1][N-1] = 1;
	for (int i=2;i<=100;i++){
		memcpy(arr[i],arr[i-1],sizeof(arr[i]));
		multiply(arr[i],N,(4*i-2));
		divide(arr[i],N,i+1);		
	}
}

int main(){
	int n;
	init();
	while(scanf("%d",&n)!=EOF){
		if(n==-1) break;
		int i=0;
		for(;arr[n][i]==0&&i<N;i++);
		//第一个数的前缀0要去掉 
		printf("%d",arr[n][i]);
		for(i=i+1;i<N;i++)
			//其他的不足4位要补足 
			printf("%04d",arr[n][i]);
		printf("\n");
	}
	return 0;
}