- 自反性:
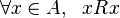
- 对称性:

- 传递性:

则称  是一个定义在
是一个定义在  上的等价关系。习惯上会把等价关系的符号由
上的等价关系。习惯上会把等价关系的符号由  改写为
改写为 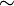 。
。
例如,设  ,定义
,定义 上的关系
上的关系 如下:
如下:
其中 叫做
叫做  与
与  模 3 同余,即
模 3 同余,即  除以 3 的余数与
除以 3 的余数与  除以 3 的余数相等。例子有 1R4, 2R5, 3R6。不难验证
除以 3 的余数相等。例子有 1R4, 2R5, 3R6。不难验证  为
为  上的等价关系。
上的等价关系。
不是所有的二元关系也是等价关系。一个简单的反例子是比较两个数中哪个较大:
- 没有自反性:任何一个数不能比自身为较大 (
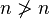 )
) - 没有对称性:如果
 ,就肯定不能有
,就肯定不能有 
阶元:
设G是群,a∈G,使得等式 ak=e 成立的最小正整数
k 称为a 的阶,记作|a|=k,称 a 为 k 阶元. 若不存在这样的正
整数 k,则称 a 为无限阶元.
与群有关的定义:
(1) 设V=<S, ° >是代数系统,°为二元运算,如果°运算是可
结合的,则称V为半群.
(2) 设V=<S,°>是半群,若e∈S是关于°运算的单位元,则称V
是含幺半群,也叫做独异点. 有时也将独异点V 记作
V=<S,°,e>.
(3) 设V=<S,°>是独异点,eS关于°运算的单位元,若
aS,a1S,则称V是群. 通常将群记作G.
ppt上50,51,52 是关于子群的证明!
关于群的中心:
对于阿贝尔群G,因为G中所有的元素互相都可交换,G的中
心就等于G. 但是对某些非交换群G,它的中心是{e}.
ppt 55:
设G是群,H,K是G的子群. 证明
(1) H∩K也是G的子群
(2) H∪K是G的子群当且仅当 HK 或 KH
maybe:一个群的子群必须含有父群的中心!
陪集:
陪集
- gH = {gh : h为H中元素 }为H在G中的左陪集,而
- Hg = {hg : h为H中元素 }为H在G中的右陪集。
仅当H为正规子群时,左右陪集相同,这也是子群正规性的一个定义。
陪集指某个G中子群的左或右陪集。因为Hg = g ( g−1Hg ),(H的)右陪集Hg和(共轭子群 g−1Hg 的)左陪集g ( g−1Hg )是相等的。因此不规定所使用的子群而讨论一个陪集是左陪集或右陪集是没有意义的。
对于交换群或者记为加法形式的群,陪集可以分别用g+H和H+g表示。
陪集就是在所有H中元素都与g在左(右)做一个运算
Lagrange)设G是有限群,H是G的子群,则
|G| = |H|·[G:H]
其中[G:H] 是H在G中的不同右陪集(或左陪集) 数,称为H在
G 中的指数.
证明图同构:
(1)顶点个数相同
(2)边数相同
(3)度数相同的顶点个数相同
(4)K度顶点的导出子图同构






















