图论中的图是一个很抽象的东西。把抽象化的东西具体化后一般都比较容易理解，比如：一张地图，这当然是很直观的了。问题在于计算机没有那么强大的功能让图直接显示，因此我们需要用特定的方式表示一张图，那计算机中如何表示一张图呢？
一般来说，有三种表示方法。
对于稠密图（就是边很多的图，对应到地图上，就是交通发达的地区图），最好用矩阵表示；
对于稀疏图（与稠密图相对，边很少的图，对应到地图上，就是鸟不生蛋的偏远地区），最好用邻接表来表示。
对于有些图，直接用边表示就可以了。比如用Kruskal算法求最小生成树存储图，一个struct edge{
int u;//表示边的起始点编号
int v; //表示边的终点编号
int w;//表示边的权值（在地图中理解为两个城市的距离）
}就OK了。
先说矩阵表示法。
矩阵表示是最直观，最容易理解的方法，也是我最喜欢的方法，也是MATLAB能高速处理的方法。
下标一般从0开始，那么定义成int graph[M][M]就可以了。
接着，第二个问题随之而来：数组中存什么？
如果只是单纯的表示点与点之间的连接关系：那么存0或者1就可以了。0表示两个点不直接相连，1表示两个点直接相连。
比如 graph[1][2]=1 就表示 图中编号为1的点与编号为2的点相连。

 

图论（二）图的表示_图论

 

以上图为例，解说矩阵表示：
矩阵表示分以下几步：
对图中的顶点进行编号：图中有V0 V1 V2 V3 V4 V5 共6个顶点。
1、 定义数据结构。
矩阵说直白一点，就是二维的数组（方阵）。比如int Graph[M][M]; M表示图中点的个数。上图中M=6。那么数组中存什么？
如果只是单纯的表示点与点之间的连接关系：那么存0或者1就可以了。0表示两个点不直接相连，1表示两个点直接相连。
比如 graph[1][2]=1 就表示 图中编号为V1的点与编号为V2的点相连。上图的存储结果即为：
 
 

 
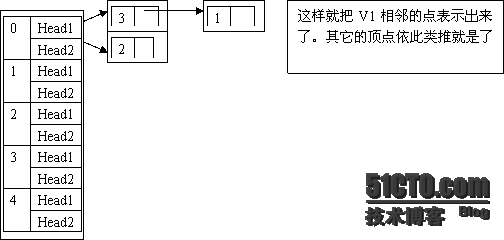
V0
V1
V2
V3
V4
V5
V0
0
1
1
0
0
0
V1
1
0
1
1
1
0
V2
1
1
0
0
1
0
V3
0
1
0
0
1
1
V4
0
1
1
1
0
1
V5
0
0
0
1
1
0

 
当然，像这样存储图就失去了一些信息，比如边的权值。所以，还可以这样存储：

 
V0
V1
V2
V3
V4
V5
V0
INF
1
4
INF
INF
INF
V1
1
INF
2
7
5
INF
V2
4
2
INF
INF
1
INF
V3
INF
7
INF
INF
3
2
V4
INF
5
1
3
INF
6
V5
INF
INF
INF
2
6
INF

其中：INF表示无穷大，也就是不直接相连。其它的值则表示两条边的权值。
 
图的邻接表表示就有点复杂了。因为如果用C/C++，则涉及到对链表的理解和掌握。
《图的基本概念及图的存储》上是这样用邻接表来存储图的，我也在博客上看到了很多都是这样的方式：（存储的是有向图）

 

  1. #define M 100  
  2. struct ArcNode{  
  3.     int adjvex;  
  4.     ArcNode *nextarc;  
  5. };  
  6. struct VNode{  
  7.     int data;  
  8.     ArcNode *head1;  
  9.     ArcNode *head2;  
  10. };  
  11. struct LGraph{  
  12.     VNode vertexs[M];  
  13.     int vexnum,arcnum;  
  14. };  
  15. LGraph lg;  
  16. void createLG(){  
  17.     int i=0;  
  18.     ArcNode *pi;  
  19.     int v1,v2;  
  20.  
  21.     lg.vexnum=lg.arcnum=0;  
  22.     scanf("%d%d",&lg.vexnum,&lg.arcnum);  
  23.     for(i=0;i<lg.vexnum;i++){  
  24.         lg.vertexs[i].head1=lg.vertexs[i].head2=NULL;  
  25.     }  
  26.     for(i=0;i<arcnum;i++){  
  27.         scanf("%d%d",&v1,&v2);  
  28.         v1--;v2--;//下标从零开始  
  29.           
  30.         pi=new ArcNode;  
  31.         pi->adjvex=v2;  
  32.         pi->nextarc=lg.vertexs[v1].head1;  
  33.         lg.vertexs[v1].head1=pi;  
  34.  
  35.         pi=new ArcNode;  
  36.         pi->adjvex=v1;  
  37.         pi->nextarc=lg.vertexs[v2].head2;  
  38.         lg.vertexs[v2].head2=pi;  
  39.     }  
  40. }  

 

我看了很久都没看明白这到底是怎么回事，后来干脆把这个结构画了出来：建议像我这样智商没达到150的，看这个的时候也自己画一画，说不定就能明白点啥！

图论（二）图的表示_图论_02

 

图论（二）图的表示_邻接表_03

 

 

在上面的表示方法中需要注意的是：下标是从0开始的：所以V1占据的下标为0，V2占据的下标为1……。
       这是可能有个疑问了：如果是无向图，怎么存储呢？
  1. #define M 100  
  2. struct ArcNode{  
  3.     int adjvex;  
  4.     ArcNode *nextarc;  
  5. };  
  6. struct VNode{  
  7.     int data;  
  8.     ArcNode *head;  
  9. };  
  10. struct LGraph{  
  11.     VNode vertexs[M];  
  12.     int vexnum,arcnum;  
  13. };  
  14. LGraph lg;  
  15. void createLG(){  
  16.     int i=0;  
  17.     ArcNode *pi;  
  18.     int v1,v2;  
  19.  
  20.     lg.vexnum=lg.arcnum=0;  
  21.     scanf("%d%d",&lg.vexnum,&lg.arcnum);  
  22.     for(i=0;i<lg.vexnum;i++){  
  23.         lg.vertexs[i].head=NULL;  
  24.     }  
  25.     for(i=0;i<arcnum;i++){  
  26.         scanf("%d%d",&v1,&v2);  
  27.         v1--;v2--;//下标从零开始  
  28.  
  29.         pi=new ArcNode;  
  30.         pi->adjvex=v2;  
  31.         pi->nextarc=lg.vertexs[v1].head;  
  32.         lg.vertexs[v1].head=pi;  
  33.  
  34.         pi=new ArcNode;  
  35.         pi->adjvex=v1;  
  36.         pi->nextarc=lg.vertexs[v2].head;  
  37.         lg.vertexs[v2].head=pi;  
  38.     }  
  39. }  

 

 

其实这种表示的方法是最烦琐的，每来了一条边，都是从头结点那里插入的，而不是接到尾巴上的。
    那如果是带权图，怎么表示呢？
在struct ArcNode{
    int adjvex;
    ArcNode *nextarc;
};
中加入一个weight就可以了：
struct ArcNode{
    int adjvex;
    int weight;
    ArcNode *nextarc;
};
其实真正用的时候，图的存储可能不用那么复杂。比如：在对图进行拓扑排序的时候，这样就可以了：
#define M 100
struct ArcNode{
    int to;
    struct ArcNode *nextarc;
};
ArcNode *List[M];
很简单吧！
    我个人觉得，图的邻接表存储，最重要的是对指针的掌握与领悟。没有指针的功底，是很难理解的，比如我！