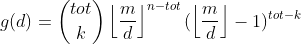bzoj4305(容斥)

原创

qkoqhh 2022-08-31 18:07:07 博主文章分类：数论 ©著作权

文章标签 #define #include 整除 文章分类 云平台云计算

©著作权归作者所有：来自51CTO博客作者qkoqhh的原创作品，请联系作者获取转载授权，否则将追究法律责任

貌似是第一次做线性容斥，还是有很多要学的。。

首先肯定是要枚举gcd的(设枚举的值为d)。。然而枚举之后发现要使数列中的gcd为1十分困难。。

而如果暂时不考虑去重的话还是可以算的，这时算出来的是gcd为d的倍数，这样的话就直接令g(d)为gcd为d的倍数的方案数，令f(d)为gcd为d的方案数

而

$g(d)=\binom{tot}{k}\left \lfloor \frac{m}{d} \right \rfloor ^{n-tot}(\left \lfloor \frac{m}{d} \right \rfloor -1)^{tot-k}$

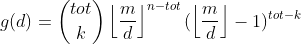
其中tot为a中能被d整除的数的个数，k为ai==bi的对数(与原题不同)

这个可以通过组合数学得到，首先要保证gcd为d的倍数，选取的数必须是d的倍数，故原序列中不被d整除的数是不可能和它相等的，然后就只能从这tot个数中选k个数，其他tot-k个数就和a不同了，故这些数都有(m/d-1)个取法，而不被d整除的位置，这时这个数可以被随意选，有(m/d)个选法。。

然后有了g(d)之后就可以算f(d)了，因为g(d)多了一些d的倍数的情况，所以要减去f(2d)、f(3d)、f(4d)....

然后问题就解决了。。

/**
 *　　　　　　  　　┏┓　　 　┏┓
 * 　　　　　  　　┏┛┗━━━━━━━┛┗━━━┓
 * 　　　　　  　　┃　　　　　　　┃ 　
 * 　　　　　  　　┃　　　━　　 　┃
 * 　　　　　  　　┃　＞　　　＜　┃
 * 　　　　　  　　┃　　　　　　　┃
 * 　　　　　  　　┃...　⌒　... 　┃
 * 　　　　　　  　┃              ┃
 * 　　　　　　  　┗━┓          ┏━┛
 * 　　　　　　　　　┃          ┃　Code is far away from bug with the animal protecting　　　　　　　　　　
 * 　　　　　　　　　┃          ┃   神兽保佑,代码无bug
 * 　　　　　　　　　┃          ┃　　　　　　　　　　　
 * 　　　　　　　　　┃          ┃  　　　　　　
 * 　　　　　　　　　┃          ┃
 * 　　　　　　　　　┃          ┃　　　　　　　　　　　
 * 　　　　　　　　　┃          ┗━━━┓
 * 　　　　　　　　　┃              ┣┓
 * 　　　　　　　　　┃              ┏┛
 * 　　　　　　　　　┗┓┓┏━━━━━━━━┳┓┏┛
 * 　　　　　　　　　　┃┫┫       ┃┫┫
 * 　　　　　　　　　　┗┻┛       ┗┻┛
 */
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
#include<cmath>
#include<map>
#include<stack>
#include<set>
#include<bitset>
#define inc(i,l,r) for(int i=l;i<=r;i++)
#define dec(i,l,r) for(int i=l;i>=r;i--)
#define link(x) for(edge *j=h[x];j;j=j->next)
#define mem(a) memset(a,0,sizeof(a))
#define ll long long
#define eps 1e-8
#define succ(x) (1LL<<(x))
#define lowbit(x) (x&(-x))
#define sqr(x) ((x)*(x))
#define mid (x+y>>1)
#define NM 300005
#define nm 220005
#define N 40005
#define M(x,y) x=max(x,y)
const double pi=acos(-1);
const ll inf=1e9+7;
using namespace std;
ll read(){
    ll x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
    return f*x;
}
 








int n,m,_t,a[NM],d[NM];
ll inv[NM],invp[NM],g[NM],p[NM];
ll qpow(ll x,ll t){return t?qpow(sqr(x)%inf,t>>1)*(t&1?x:1)%inf:1LL;}

int main(){
    n=read();m=read();_t=read();_t=n-_t;
    p[1]=p[0]=inv[1]=invp[1]=invp[0]=1;
    inc(i,2,max(n,m))p[i]=p[i-1]*i%inf,inv[i]=inv[inf%i]*(inf-inf/i)%inf,invp[i]=invp[i-1]*inv[i]%inf;
    inc(i,1,n)a[read()]++;
    inc(i,1,m)for(int j=i;j<=m;j+=i)d[i]+=a[j];
    inc(i,1,m)if(d[i]>=_t){
    g[i]=p[d[i]]*invp[_t]%inf*invp[d[i]-_t]%inf;
    g[i]*=qpow(m/i,n-d[i]);g[i]%=inf;
    g[i]*=qpow(m/i-1,d[i]-_t),g[i]%=inf;
    }
    dec(i,m,1)for(int j=i<<1;j<=m;j+=i)g[i]+=inf-g[j],g[i]%=inf;
    inc(i,1,m-1)printf("%lld ",g[i]);printf("%lld\n",g[m]);
    return 0;
}