因子分析是一种统计方法,可用于描述观察到的相关变量之间的变异性,即潜在的未观察到的变量数量可能更少(称为因子)。例如,六个观察变量的变化可能主要反映了两个未观察(基础)变量的变化。因子分析搜索这种联合变化,以响应未观察到的潜在变量。将观察到的变量建模为潜在因素以及“错误”项的线性组合。
简而言之,变量的因子加载量化了变量与给定因子相关的程度。
因子分析方法背后的一个普遍原理是,有关观察到的变量之间的相互依赖性的信息可以稍后用于减少数据集中的变量集。因子分析通常用于生物学,心理计量学,人格理论,市场营销,产品管理,运营研究和财务。在有大量观察到的变量被认为反映较少数量的基础/潜在变量的数据集时,这可能会有所帮助。它是最常用的相互依存技术之一,当相关变量集显示出系统的相互依存关系时使用,其目的是找出产生共同性的潜在因素。
因子分析分为两类

因子分析重要部分是二变量相关性矩阵和因子的相关性
pattern matrix中灰色部分就是变量值高的,灰色变量具有代表性
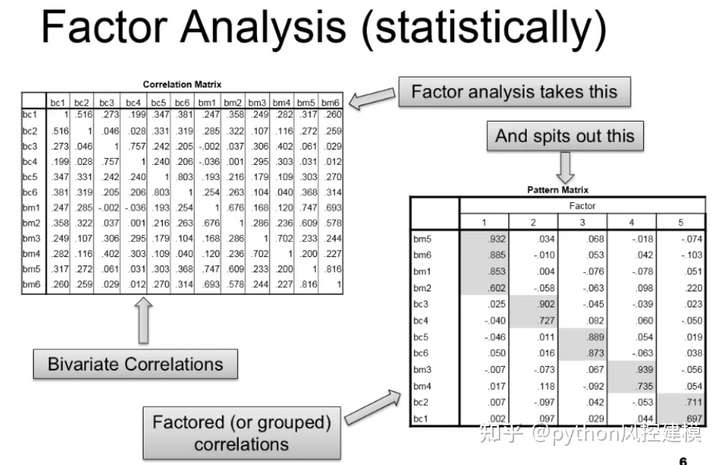


因子分析是一种相关性分析方法,用于在大量变量中寻找和描述潜在因子
因子分析确认变量的相关性,把相关性强的变量归类为一个潜在因子

最早因子分析应用于二战后IQ测试。一般来说,大量变量可以降维到少数几个因子。

因子分析有6个假设条件,
1.没有异常值
2.足够样本量
3.没有完美多重共线性
4.不需要符合方差齐性
5.变量符合线性
6.数据符合间隔性
当然,这是一个理想状态,实际应用中,很难做到完全遵从。如果因子分析模型效果不好,就要反思一下这6个假设条件是否存在严重问题。

因子分析与机器学习建模项目实战,我通过乳腺癌数据集,测试因子分析降维后,模型性能是否有限制下降。
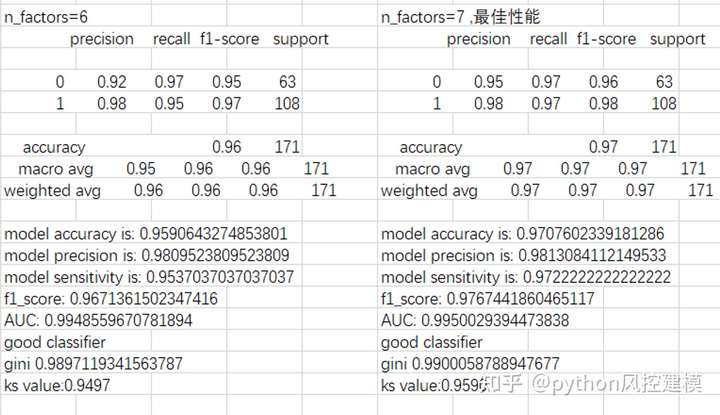
结果惊讶发现,模型性能不但没有下降,而且还有提升。因子分析让模型降维,数据量减少,内存减少,运行和预测更快,模型部署难度降低,模型部署验证难度降低,企业开发模型时间成本降低,可谓一石十鸟。下图是因子分析模型调参的部分展示。
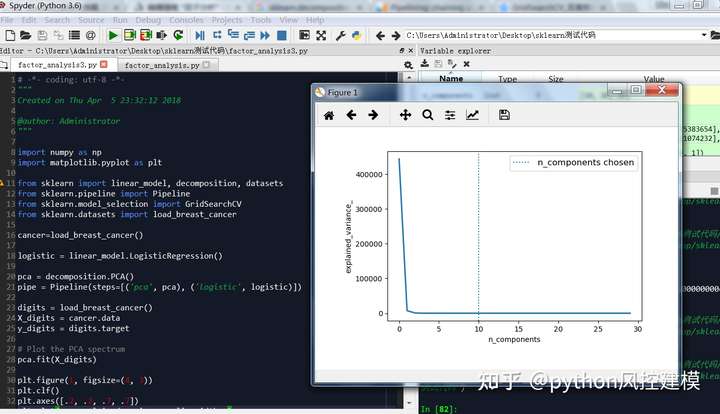
下图是python绘制因子分析碎石图。我们选因子时,要选特征值大于1的因子。但实际建模中,可以有一定灵活空间。
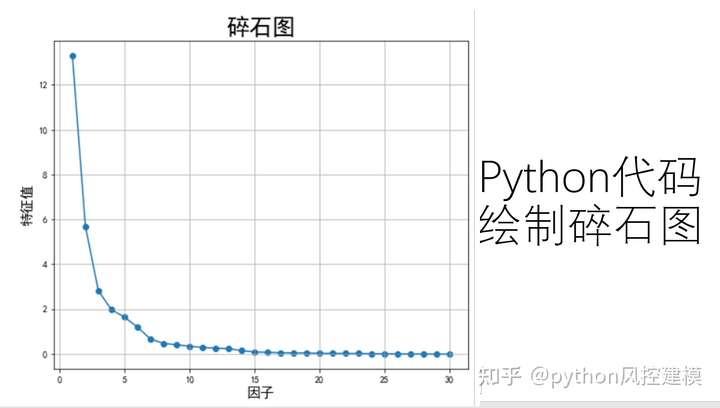
累计方差贡献,我们看到第七个因子fac7的累计方差贡献已经达81.872%,超过80%。因此7个因子可以解释原始变量81.872%成分,效果非常不错。

欢迎学习完整版《python实战因子分析和主成分分析》




















