(ST表求区间最值)AcWing 1273. 天才的记忆

输入样例：

6
34 1 8 123 3 2
4
1 2
1 5
3 4
2 3

输出样例：

34
123
123
8

百度百科中对ST算法的解释

简而言之,

首先通过初始化,我们赋予f[i][j]如下特性: 表示要查询的原数组下标i及其之后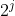长度的区间(即 下表区间[i, i+(1<<j)])中的最值

那么如何知晓这个区间中的最值呢?

这个问题进一步细化为求max{ f[ i][ j-1], f[ i+(1 << j-1)][ j-1] },即在两部分长度均为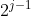的区间比大小

当我们查询区间[ L, R]的时候, 只需要从两段长度均为log以二为底的(R-L+1)的区间中找到最大值即可,这两段区间一个是以L为起始,另一个是以R为终止,可能有覆盖也可能不覆盖, 但是可以保证整个[L,R]区间内的值均在考虑范围之内, 如下

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;

const int N = 2e5+10, M = 18;
int n, f[N][M], w[N];

int search(int l, int r)
{
    int len = r-l+1;
    int k = log(len)/log(2);
    return max(f[l][k], f[r-(1<<k)+1][k]);
}

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i ++) scanf("%d", &f[i][0]);
    for(int j = 1; j < M; j ++)
        for(int i = 1; i+(1<<j)-1 <= n; i ++)
            f[i][j] = max(f[i][j-1], f[i+(1<<j-1)][j-1]);
    
    int t;
    cin >> t;
    while(t --)
    {
        int l,r;
        scanf("%d%d", &l, &r);
        cout << search(l, r) <<endl;
    }
}